如何保证启闭件的良好密封性？

当阀门的结构设计已定，零件的主要尺寸、部件行程、密封圈零件的材料、填料尺寸、阀杆螺纹的直径和螺距等确定之后，阀门的作用力计算是一种校核计算，其任务是要确定必须的电动力矩、手动手轮的直径、液压或气压缸的直径、远距离驱动时在轴上所必须的力矩、手动或电动时减速箱的减速比以及阀门的启闭时间等。计算按下列步骤进行：

1）明确阀门的工作条件，确定对密封和结构的技术要求以及密封圈材料和尺寸、工作介质的性质和介质的动力参数。

2）计算出为启闭件密封所必需的作用于阀瓣、楔式闸板、圆盘上的力F_y。

3）计算为产生F_y所必需的作用于阀杆或轴杆上的力F_MT。

4）确定为移动阀瓣所必须的作用于阀杆上的总作用力F₀，这时要把填料的摩擦力F_T考虑进去。

5）计算产生总作用力F₀所必须的、作用于阀杆上的力距M。

6）确定所求的结构参数：驱动机构的转矩、减速箱的减速比、手轮直径、气缸直径等。

当明确阀门的工作条件时，应当规定出阀门的用途、工作介质及其性质、工作压力及温度、密封等级、运行强度（动作次数、启闭循环次数）、可靠性和耐久性要求、开启时的压力降等，以及在截止阀内介质的流动方向、密封圈材料、材料的磨损度、密封圈材料的最大许用比压值、阀杆和阀杆螺母的几何参数及所用材料、填料箱部位的几何尺寸或波纹管的尺寸等。

当选择带直线运动输出杆的气动、液动驱动装置时运用F₀值，而当选择带转动的气动、液动装置时，则运用M值。在远距离操纵的驱动装置上，转矩M_a=M/η，式中的M为阀门的力矩，η为远距离操纵驱动装置的传动效率。

切断阀的主要任务是对管路进行有效的截流，使其不漏。在核动力装置的主回路上，启闭件的密封面是靠熔焊在阀座上的金属圈或焊到阀体上的制成单个形式的密封圈来实现的。密封圈的密封面上堆焊高强度的镍基硬质合金，再将其表面研磨到表面粗糙度值Ra不大于0.1mm。

密封圈的表面可做成平面或锥面。在计算时所采用的半经验关系式是由实验数据的结果获得的。在温度为20℃的某种介质和采用经济合理的表面粗糙度值（Ra=0.08～0.16mm）的前提下，把在密封圈接触面上所产生的密封比压值q作为给定条件下决定连接处密封度的主要因素。对于金属对金属的密封，把介质压力和密封面的宽度作为该连接形式的变量。为考虑真实参数与确定参数（介质、温度、表面粗糙度值）偏差的影响，可采用一定的修正系数。

实验表明，在表面粗糙度值相同的情况下，其q值相应分散，这说明对密封性能的影响除表面粗糙度值外，还有密封圈表面的平面度和面轮廓度等因素，除前面已采用的参数Ra以外，还可以给定其他参数：如平面度公差，无基准的面轮廓度公差。考虑到这些参数之后而作出的对表面粗糙度的评价会更确切，从而能提高确定q的精确度。

假定接触面上的密封比压均匀分布，确定保证接合面的密封所必须的力，可按下式计算：

F_m=A_pq_F

式中 A_p——密封面的接触面积（mm²）：

A_p=πD_pb

式中 D_p——密封面的平均直径（mm）；

b——密封面的宽度（mm）；

q_F——保证结合面密封所必须的密封比压（MPa）。

q_F值取决于密封面材料的物理力学性能，而对于各种类型的钢来说，可采用一种q_F值，其误差也不会很大。在q_F的作用下形成一个密封带，阻止介质流过，介质压力愈高，q_F值则应愈大。

单阀座阀门介质应从阀瓣的下面流经阀门，如截止阀、控制阀、直接作用式安全阀。对于双阀座阀门和某些单阀座阀门，如闸阀、球阀、旋塞阀和蝶阀，可不必考虑介质的流向。在前一种情况下，产生的强制密封，要克服由介质压力而引起的作用力；在第二种情况下，是在介质压力作用下采用连接面的自紧密封。只有满足F_J≥F_m的条件，才能保证密封

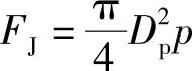
式中 F_J——由介质压力产生的力（N）；

p——介质工作压力（MPa）。

当介质从阀瓣下方进入的阀门要进行作用力的计算时，要保证密封所需阀杆的轴向力

F=F_m+F_J

在实验数据的基础上可以提供F（p）的关系曲线图，如图3-1所示，对于每一个p值，F值是由两段组成，直线F_J以上的一段F_m和直线F_J以下的一段F_J。

F_J的值是由直径D_p和介质压力p来确定，因此，为了计算F的值，必须定出F_m的值。分析F_m对弄清密封连接的密封机理也有益处。一般假定F_m沿密封面均匀分布，因此，在它的上面所产生的密封比压q_F为

q_F=F_m/πD_pb

假定介质能渗入到两个相接触的密封面之间，工作介质的压力作用到沿直径为D_p的圆周线的某个面积上。这个面积值，事先不知道，当采用非金属密封圈时，这个值可能接近于零，当采用刚性金属密封圈时，这个值可能大于接触面积的一半。由于密封比压q_F是按密封面面积所取的平均值，所以它是对密封面的整个接触面积A而言的，忽略了介质在密封圈表面部分渗入的可能性。

图3-1 在不同的密封表面质量下的F（p）关系曲线

1—好的密封表面 2—较差的密封表面 3—不好的密封表面

当计算阀门的必须比压时，采用下列公式来确定q_F值：

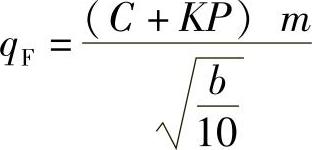
式中 C——对于给定的密封面材料是个常数值，它表征在低的介质压力下密封面所必须的最小密封比压（MPa）；

K——对于给定的密封面材料，考虑到介质压力对密封比压的影响系数；

m——考虑到计算条件与定为标准条件之间的差异系数，即温度升高，表面粗糙度值和密封面直径等偏差的影响；

p——介质的工作压力（MPa）；

b——密封面宽度（mm）。

对于钢和高强度合金堆焊的密封面，当在水中试验时，C=3.5，K=1；对于氟塑料密封圈在煤油里试验时，C=2.0，K=1.5。当在冷热变换条件下采用氟塑料密封圈来密封时，要求密封比压比密度不变的条件要高出几倍。这是因为氟塑有蠕变，当冷热变换时，密封圈产生压缩和塑性变形，因而密封性能受到破坏。

对于中等压力和中等宽度的钢制密封圈，在水中试验时，上述公式能给出十分满意的结果，如果密封面的表面粗糙度值Ra在0.08～0.16μm，则阀门的密封性能可达到ISO5208—2008的B级。在温度提高、高渗透力的液体或气体（过热蒸汽、氢气、氦气等）、脏介质及其他特殊条件下，要引入运行条件和工作介质的修正系数。

由前苏联Д.Ф.古列维奇所做的试验表明，q_F（p）的关系曲线具有普遍的规律性，对于可拆卸的连接密封，无论采用金属材料还是非金属材料（橡胶、氟塑料等）它可由图3-2上的曲线表示出来。

典型的综合曲线q_F（p）不通过坐标原点，当p=0时，它的纵坐标截距q_A=a。曲线可分成三个特征段，第1段AM是斜角为φ的近似直线，第2段MN是线段AM的纵坐标为q_N的水平线NT的过渡线。线段的长短，φ的值以及过渡曲线MN的特征取决于材料性质、密封面的表面粗糙度和平面度，以及启闭件的结构。

母材金属在线段AM上将会产生弹性变形，相接触表面平面度的公差将会减小，纵坐标的截距值恰好是产生“初始密封性”的密封比压，这时介质压力对密封性的影响还不大，实际上当q_F=q_A时，产生的全部力的作用完全用于消除密封面处的微观缝隙。随着介质压力的提高，工作介质破坏密封性能的作用会增强，而q_F提高，形成AM曲线。

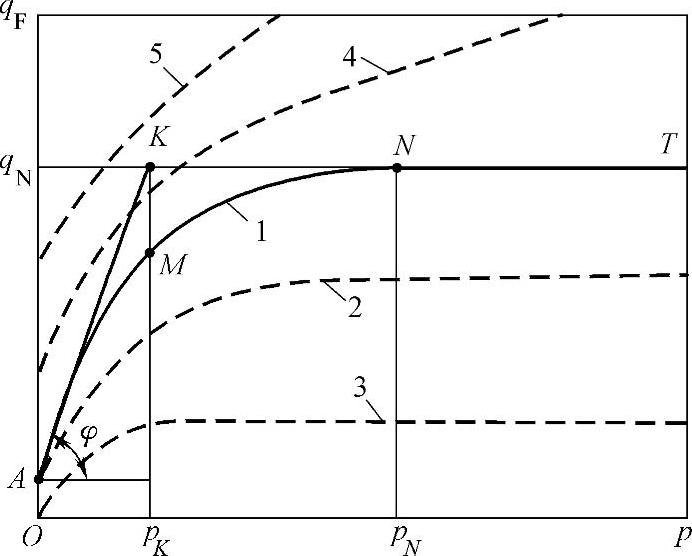
图3-2 q_F（p）的典型综合关系曲线

1—密封圈的组装和表面粗糙度为标准的 2、3—密封圈的组装更加细心，但表面粗糙度值Ra比一般的高 4、5—密封圈的组装质量较差，但表面粗糙度值Ra比一般的低(www.xing528.com)

“完全密封”线段NT符合于比压q_F不随介质压力变化的条件，即所有可能的微观缝隙均已消除，对于全部p值在q_F为常量的条件下密封性能都能得到保证。过渡曲线所对应的是既有弹性变形又有塑性变形。

在一定的压力范围内，曲线可近似地用下列方程来描述：

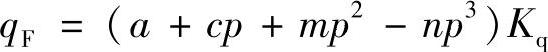
或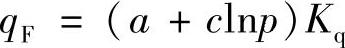

式中a、c、m、n——系数；

K_q——考虑各种因素（密封面宽度、温度等）对q_F的影响的综合系数。

为了在最小表压下保证密封性能，必须有一定的初始密封比压，它的值取决于密封面的表面粗糙度和平面度。在图3-2上用虚线表示出的曲线2和3代表比一般更小的表面粗糙度和特别精致的组装；而曲线4和5表示具有较粗糙的组装。组装质量越低，则曲线也越高越陡，M点也越向右移。

对于截止阀类的阀门，当在阀瓣上采用平面密封，而密封面宽度b=2～6mm时，其密封试验的结果曲线与图3-2上的曲线形式一致。基于这些试验数据，当采用钢制平面圆环密封，其表面粗糙度值Ra为0.08μm时，对于水介质，推荐使用下列公式：

当压力p≤2.5MPa时

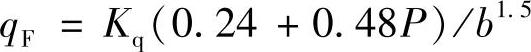
当2.5MPa＜p＜16.0MPa时

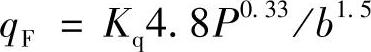
综合系数可写成分系数的乘积形式

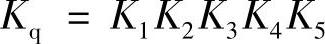
各分系数是考虑下列因素对密封性的影响：

K₁：对表面粗糙度的影响，当表面粗糙度值Ra值为0.1μm时，K₁=1；当Ra为0.05μm时，K₁=0.8；当Ra为0.2μm时，K₁=1.2；

K₂：对与密封面直径D_p有关的各种因素（平面度、组装质量等）的影响。当D_p=100mm时，K₂=1；对于其他的值，在获得准确试验数据前也取K₂=1；

K₃：对介质的影响。对于水K₃=1；对于空气K₃=1.4；对于蒸汽K₃=1.7；对于氢气和氦气K₃=2.0；

K₄：对工作介质温度的影响。t=20℃时K₄=1；其他温度时，在获得准确的数据前可采用K₄=1；

K₅：对考虑阀门的重要程度：对于工艺管线上的阀门，K₅=1.2；对于重要的对象、有毒介质、易燃易爆介质的阀门，K₅=1.5；对于特别重要的装置，K₅=1.8。

实际的密封比压q，不应大于K₅q_N的值，这里q_N为达到“完全密封”时的比压，见图3-2，同时也不应大于[q]，[q]为密封面材料的许用比压值，即满足下列条件：

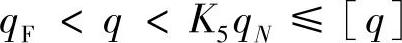
在表3-1中列出了K_q=1时q_F的值，而在表3-2和表3-3中列出了[q]的值。

表3-1 在水中保证钢制平面密封所必须的密封比压值q_F

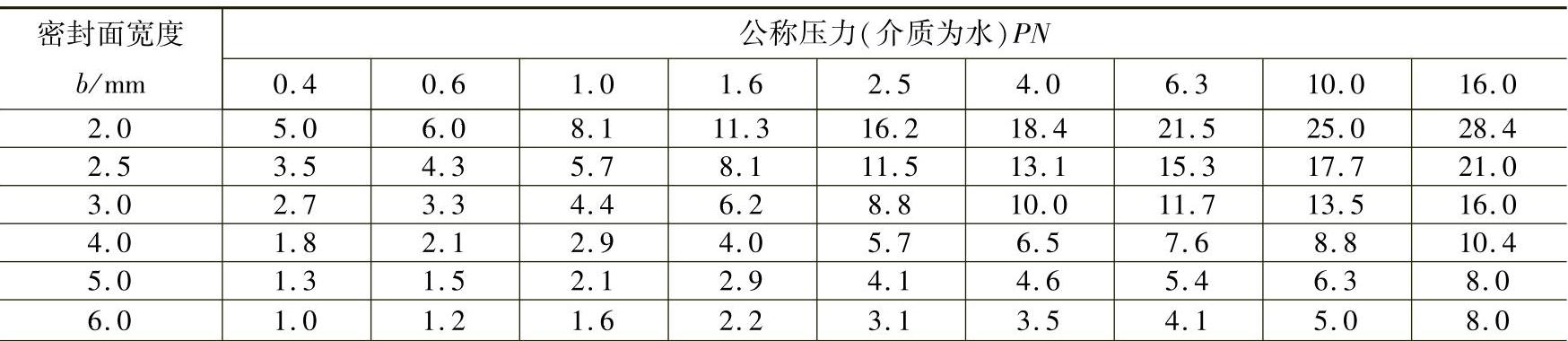
表3-2 在≤200℃时，在闸阀和截止阀的钢制密封面上的许用比压值[q]

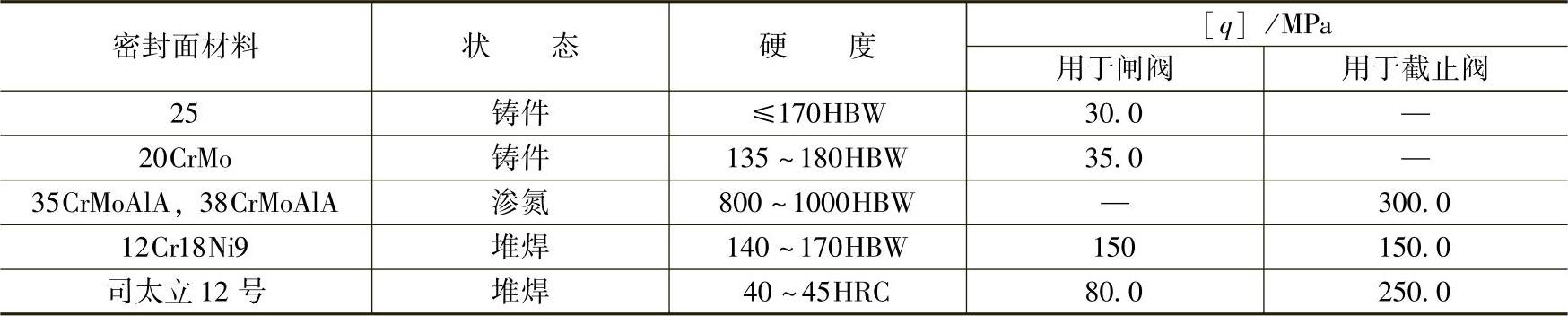
表3-3 聚四氟乙烯密封圈许用密封比压值[q]

在高压介质条件下，在截止阀的阀座上常采用倒角为90°的圆锥形密封面，其宽度约为0.5mm，而阀瓣则采用锥面，这种密封形式的密封试验结果如图3-3所示。这里使用的准则不是密封比压q_F，而是作用在每毫米密封线上的接触作用力q₁，q₁与介质压力p的关系曲线特征，如同平面密封一样。在介质压力为20.0MPa以下，倒角宽度为0.5～1mm、密封面堆焊司太立12号或司太立6号合金、表面粗糙度值Ra为0.1μm、工作温度t≤350℃时可采用下列公式：

当P≤2.5MPa时

q₁=1.0+4.5p-0.1p²

当2.5＜p＜20.0MPa时

q₁=5.0+0.9p-0.003p²在表3-4上，给出了对应于上述公式的q₁值。

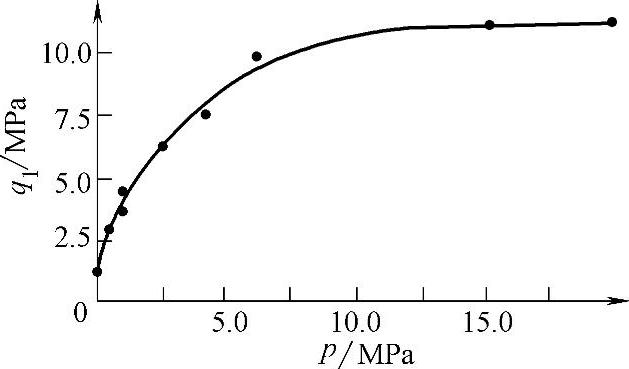
图3-3 在阀座密封面上，宽度b=0.5mm的带倒角金属圆锥形密封面的q₁（p）关系曲线

表3-4 单位密封线长度上的作用力q₁（圆锥角90°，密封面宽度b=0.5～1mm）

由于介质压力在阀瓣上的作用假定按密封面的平均直径D_p计算，因而计算出的密封比压q_F不应小于p/2。否则，当密封面的宽度很窄时，介质压力可按密封面外径所包含的面积分布时，实际作用力就可能大于计算的作用力，这样，公式

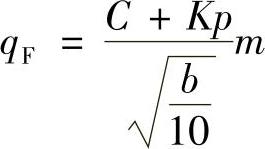
仅代表q_F=f（p）关系综合曲线的初始段落。这里q_F值大致正比于p。p对必须的密封比压q_F影响减小，可以解释如下，随着介质压力的提高，出现了弹性变形，这时密封表面的预压缩起着特别显著的作用。当关闭时，如还没有向阀施加介质压力时，在密封面上应该产生的初始密封比压为q₀=F_m/A，而施加介质压力后，q_F=（F_m+F_J）/A，由于F_m=πD_pbq_F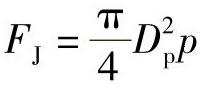，，所以

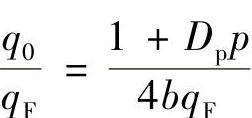
这样，在同样的q_F值条件下，随着介质压力p的提高和D_p的增大，

的比值也增大。当施加介质压力前密封表面工作在弹性变形状况下，预紧比压具有重要的意义，因为这种弹塑性变形决定着相互接触的两密封面的吻合度。

为了能密封地截断介质，要求的比压比不密封时要高得多。这可以这样来解释：当“密封”时，不产生较高的初始密封比压q₀，此外，当“密封”时，介质压力作用的初始面积直径可能大于D_p，接近于密封面的外径。有一个重要的情况是，在阀瓣和阀座的密封面之间残存的液体也必须要压紧，当它之间的缝隙很小时，在其中产生高压必然阻止两密封面的相互贴近。

不同类型阀门的密封比压的计算，要考虑它的具体结构尺寸及其工作条件。计算方法和采用的公式在《阀门设计入门与精通》一书中已给出。由于波纹管密封结构的阀门在核动力装置中具有代表性，因此，下一节将给出这类阀门作用力的计算。