可压缩流体特性及质量流量计算

可压缩介质的流动有非阻塞流和阻塞流两种情况，在这两种情况下所用的计算公式是不同的。当X＜F_KX_T时，不会产生阻塞流；当X＞F_KX_T时则产生阻塞流。F_K为比热比系数，空气的F_K=1，对非空气介质（κ是气体等熵指数）；X_T为临界压差比，见表2-10。

表2-10 压力恢复系数F_L和临界压差比X_T

根据国际电工委员会标准（IEC 534-22），在安装条件下，可压缩介质流量系数的计算式为

或

或

式中 C——流量系数（包括A_V、K_V、C_V），单位各不相同；

q_m——质量流量（kg/h）；

q_V——体积流量（m³/h）；

F_p——管道几何形状系数，量纲为1；

y——膨胀系数，量纲为1；

X——压差比（压差与入口绝对压力之比），X=Δp/p₁，量纲为1；

p₁——阀前压力（kPa）或（bar）（1bar=10⁵Pa）；

ρ₁——介质在p₁和T₁时的密度（kg/m³）；

T₁——阀入口的热力学温度[K（℃+273）]；

M——介质相对分子质量；

Z——压缩系数，量纲为1；

N₆、N₈、N₉——数字常数，其值见表2-11。

表2-11 数字常数N

1.气体

（1）非阻塞流 当X＜F_KX_T时，是非阻流情况，如果采用法定计量单位制，则计算公式为

或

或

式中 q_VN——气体标准体积流量（m³/h）；

ρ_N——气体标准状态下密度（273K，1.013×10²kPa）（kg/m³）；

p₁——阀前绝对压力（kPa）；

X——压差比，X=Δp；

p₁

y——膨胀系数；

T₁——入口热力学温度（K）；

M——气体分子量；

G——气体的相对密度（空气为1）；

Z——压缩系数。

压缩系数Z是比压力和比温度的函数，可从图2-22中查出。

比压力的定义是：实际入口绝对压力p₁与所述介质的绝对热力临界压力之比；而比温度的定义是入口温度T₁和热力学临界温度T₂之比。若比压力为p_r，比温度为T_r，则

图2-22 压缩系数图

a）比压力p_r为0～10 b）比压力p_r为0～40

由于式（2-30）、式（2-31）及另一些计算式都不包含上游条件时介质的实际密度这一项，而密度是根据理想气体定律由入口压力和温度导出的。在某些条件下，真空气体的性质与理想气体的偏差很大。在这些情况下，要引入压缩系数Z来补偿这个偏差。

膨胀系数y用来校正从阀门的入口到阀后缩流处气体密度的变化，理论上y值和节流口面积与入口面积之比、流路形状、压缩比X、雷诺数、比热系数F_K等因素有关。由于气体介质流速较高，在可压缩流情况下，由于紊流几乎始终存在，所以雷诺数的影响极小，可以忽略不计。其他因素与y的关系可以表示如下：

式中 X_T——临界压差比，查表2-10；(www.xing528.com)

X——压差比；

F_K——比热比系数，空气的F_K=1，对非空气介质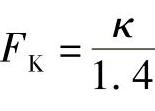：（κ是气体的等熵指数）。

（2）阻塞流 当X≥F_KX_T时，即出现阻塞流情况。

如果阀前压力p₁保持不变，阀后压力逐渐降低，气流就慢慢形成了阻塞流。即使这时阀后压力再降低，流量也不会增加。在压差比X达到F_KX_T值时就达到极限值。使用公式时，X值要保持在这一极限内。因此，y值只能在0.667（当X=F_KX_T时）到1.0的范围内。

在阻塞流情况下，流量系数的计算公式可简化为

或

或

注意，X_T值可通过空气试验来确定，也可以利用无连接管件控制阀的液体压力恢复系数F_L近似求得。

如果一个控制阀装有渐缩管或其他管件，X_T就会受到影响。这时的X_T值就标为X_Tp。

为达到规定的±5%的允差极限，阀和连接管件应作为一个整体进行试验。如果允许用估计值，可采用下式：

在上面的公式中，X_T为不装渐缩管或其他管件的控制阀的压差比，系数ζ₁是连接阀入口侧的渐缩管或其他管件的流阻系数。

2.蒸汽

根据膨胀系数法，以质量流量为单位，可推导出下面的计算公式：

（1）当X＜F_KX_T时（非阻塞流）

（2）当X≥F_KX_T时（阻塞流）

式中 q_ms——蒸汽的质量流量（kg/h）；

ρ_s——阀前入口蒸汽的密度（kg/m³）；

κ——蒸汽的等熵指数。

如果是过热蒸汽，应代入过热条件下的实际密度。

3.两相流体

当控制阀的介质为气液两相的混合流时，过去一般都采用分别计算液体和气体（蒸汽）的C值，然后相加作为控制阀的总流量系数值。这种分别计算液体及气体的流量系数，然后相加的方法是基于两种介质单独流动的观点，没有考虑到它们的相互影响。实际上，当气相大大多于液相时，液相成为雾状，具有近似气相的性质；当液相大大多于气相时，气相成为气泡而夹杂在液相中间，这时具有液相性质，此时用上面的计算方法计算误差也较大。前者偏大而后者偏小。因此，两相流体流量系数的计算必须考虑到两相流动之间的相互影响，寻找有效而准确的计算方法。

按照新的膨胀系数的理论，目前对两相流的流量系数计算多采用有效密度法或两相密度法。当液体和气体（或蒸汽）均匀混合流过控制阀时，液体的密度保持不变，而气体或蒸汽由于膨胀而使密度下降，因此，要用膨胀系数加以修正。从式（2-42）可知，质量流量与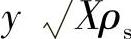成正比，如果这时气体的有效密度为ρ_e，则

即

在其他条件相同的情况下，密度为ρ_s的可压缩介质的质量流量与密度为ρ_e的不可压缩介质的质量流量是一样的，因此，对于均匀混合的气（汽）、液两相介质可按混合介质的有效密度ρ_e进行计算。当两相流中为液体和蒸汽，而液体占绝大部分时，可以用阀入口（p₁和T₁条件下）的两相流密度ρ_m来计算。

总之，计算的前提条件是：气（汽）、液两相介质必须均匀混合，而且其中每一单相介质均达到阻塞流条件，计算公式如下：

（1）液体与非液化性气体 先决条件：液体Δp＜F²_L（p₁-p₂），气体X＜F_KX_T，两个条件都能满足

式中 q_mg——气（汽）体的质量流量（kg/h）；

q_mL——液体的质量流量（kg/h）；

ρ_e——混合介质的有效密度（kg/m³）。

或

或

（2）液体与蒸汽 当蒸汽占两相混合介质的绝大部分时，用式（2-48）进行计算。对液体占绝大部分的两相混合介质，计算公式为

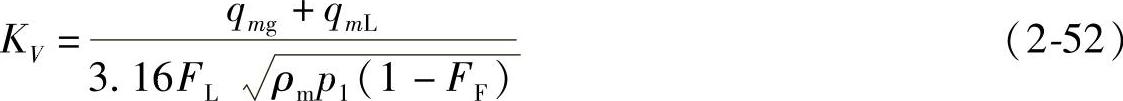
式中 ρ_m——两相流介质密度（kg/m³）

或

或