阀门元件对流体阻力的影响

阀门流阻系数ζ用以表示阀门对通过液体的阻力，流阻系数ζ的大小取决于阀门的结构和尺寸以及决定液流直线性的体腔结构与形状、等截面性等。对于每一种结构的流阻系数ζ都要用试验方法确定。

在一定程度上可以认为，阀门体腔内的每个零件可以看作一个产生阻力的元件系统（流束的转弯、扩大、收缩、再转弯等），因此阀门的压力损失，大致等于阀门各个零件压力损失的总和。阀门的总阻力系数可近似地看作是各个零件阻力系数的总和，即

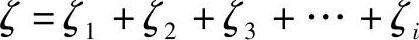
式中 ζ₁、ζ₂、ζ₃…——在管路中介质流速相同的情况下，阀门中各零件的阻力系数。

应该指出，阀门中一个零件的阻力发生变化，就可能使阀门的阻力改变或重新分布，也就是说介质流在各管段是相互影响的。

为了评定组成零件对阀门阻力的影响，可根据其形状和尺寸比例列出最常见的零件阻力数据，计算时，ζ值必须与截面和流速正好对应。将某一截面的ζ值用于其他流速，则可能产生很大的误差。

（1）流束突然扩大 如图2-15a所示，流束突然扩大，会产生最大压力损失。在这种情况下，介质部分流速消耗在涡流形成、液体的搅动和使液体升温上。局部阻力系数和扩大前管路的截面积A₁和扩大后管路截面积A₂之比的近似关系式表示如下：

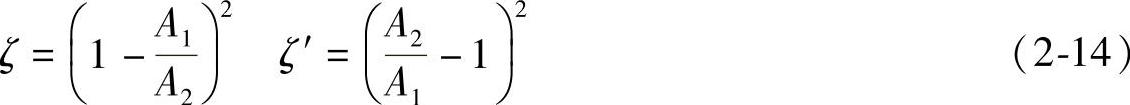
式中 ζ——扩大前管路内与介质流速有关的流阻系数，见表2-3；

ζ′——扩大后管路内与介质流速有关的流阻系数。

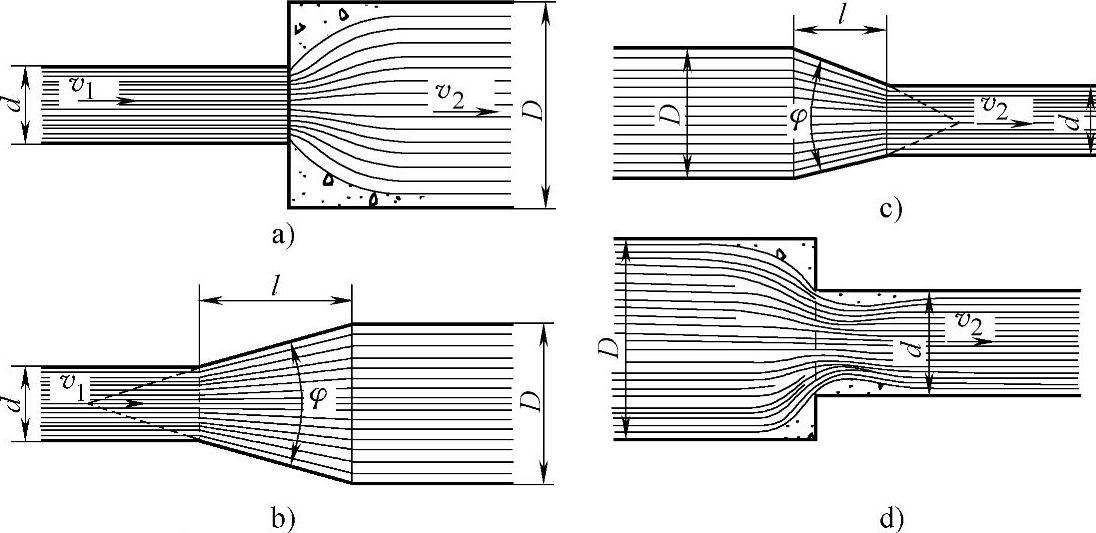
图2-15 液体在过渡区内流动的示意图

a）突然扩大 b）逐渐扩大 c）逐渐缩小 d）突然缩小

表2-3 突然扩大时的局部流阻系数ζ值

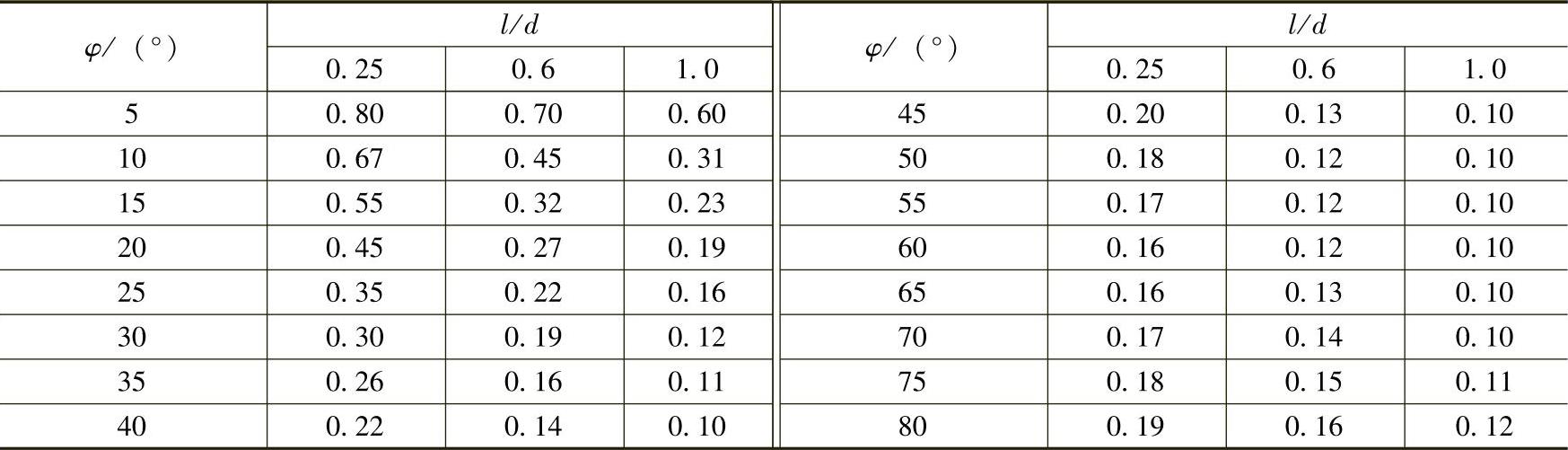
（2）流束逐渐扩大 流束逐渐扩大比突然扩大产生的压力损失要小，如图2-15b所示。所以，应使锥体部分长度l尽可能长些，即尽量以φ角小些的锥形渐缩管来替代突然扩大的异径管。

在角度很小（φ≤12°）时，可近似地取

式中 A₁——扩大前管子的横截面积（mm²）；

A₂——扩大后管子的横截面积（mm²）；

φ——过渡部分的锥角（°）。

渐扩管的总压头损失包括扩张损失和摩擦损失，由此

ζ=ζ_P+ζ_T

式中

。

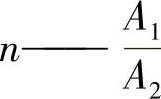当扩大角φ=0°～25°时

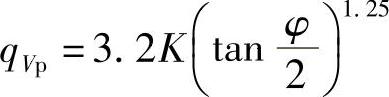
式中 K——入口条件对流阻系数的影响系数，K=1～2。

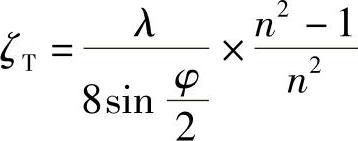(www.xing528.com)

式中 λ——渐扩管单位长度的摩擦阻力系数。此系数决定于Re_D和管壁的表面粗糙度。

渐扩管φ角大于40°时，阻力较大，因此不宜采用。在必须安装扩张角φ＞40°的短渐扩管时，则采用突然扩张式更为适宜。

（3）流束逐渐收缩 如图2-15c所示，流束逐渐收缩产生的压力损失一般不大。在锥角φ＜5°和异径圆管光滑过渡的情况下，压力损失仅来源于摩擦。此时，取ζ′=0.06～0.005。收缩后的介质流速的流阻系数ζ′可按下式确定：

式中 η——入口的减缓系数，见表2-4。

表2-4 入口的减缓系数η值

（4）流束突然缩小 如图2-15d所示，产生的流体阻力取决于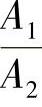的截面比。与收缩后的液流流速有关的流阻系数ζ′按式（2-18）确定：

（5）管路均匀圆滑转弯 如图2-16a所示，产生的阻力取决于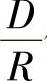值，即管道直径与弯曲半径的比值和管道弯曲处的转角。由于液体流动的摩擦力、惯性力以及流速差的作用，在管

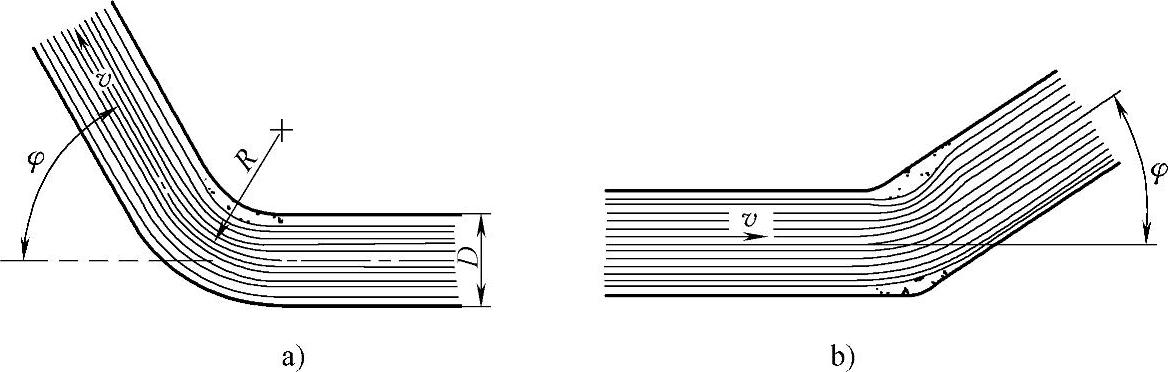
图2-16 管路转弯

a）圆滑转弯 b）急转弯

道转弯处沿弯管内外边形成涡流。这些涡流产生附加阻力而且形成弯管流体中的死区。在转弯流动的阀门中，沿转弯半径方向形成接近于矩形四边形的矩形截面较为合理。

对于不变截面的圆管，在转弯为90°和D≤2R≤5D时的局部阻力系数，见表2-5，可近似地按式（2-19）求出：

假如转弯不等于90°时，则

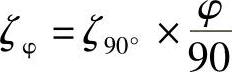
对于直径为100～1000mm，转角φ=90°的弯管，阻力系数ζ=0.4～0.5。

（6）管路急转弯 如图2-16b所示，在锻制和焊接的阀门中，由于锻造阀门的介质流道是用钻孔方法获得，局部阻力系数见表2-5，可近似地按下式求出：

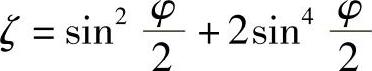
对称的锥形短管（见图2-17）及类似的阀门缩口通道，其阻力系数可按式（2-20）确定：

式中 A_c——按缩口直径D_c计算的截面积。

表2-5 管路转弯时局部阻力系数ζ值

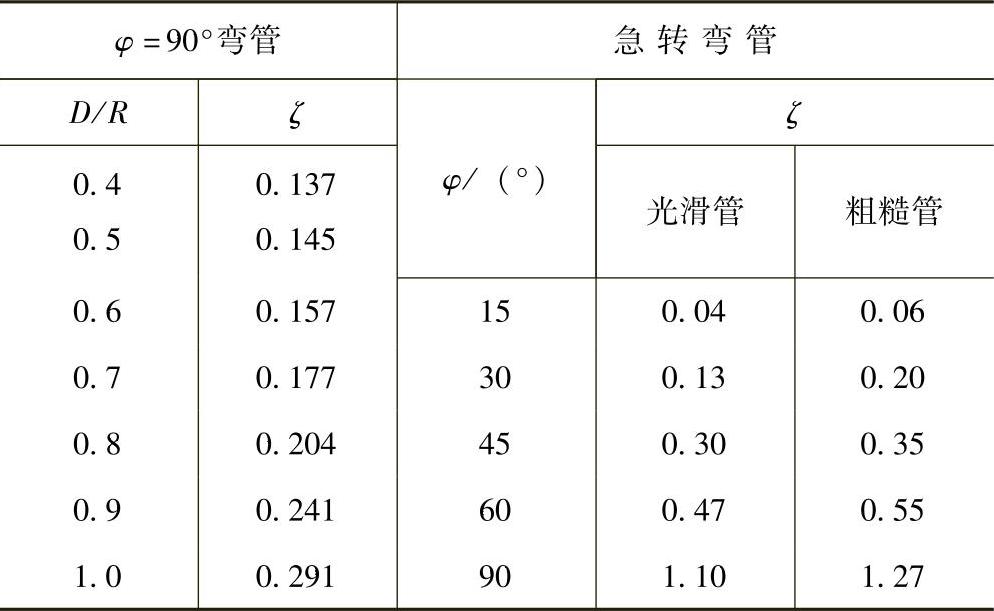
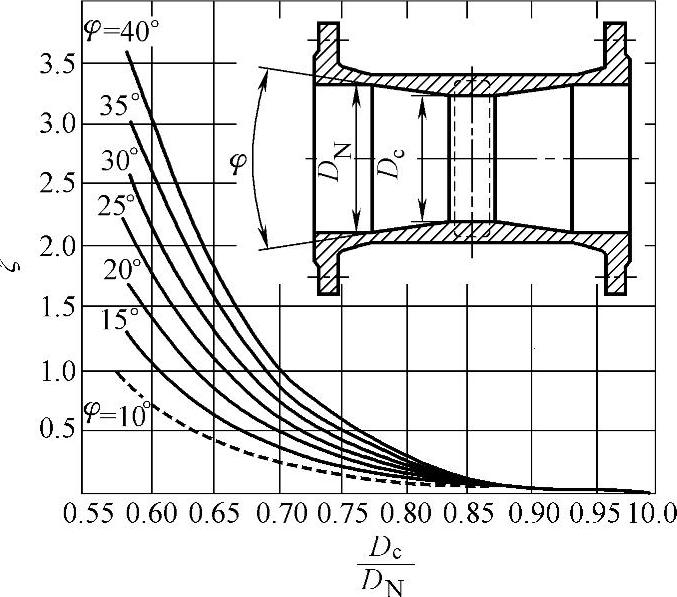
图2-17 对称的锥形短管及缩径阀门的阻力系数ζ变化曲线图