阀门流体计算原理详解

阀门的流体计算是确定与阀门的水利特性相关参数的过程。阀门的所有流体计算均以几个基本公式为依据，并根据阀门的类型和工作条件又有所不同。

在最简单的情况下，即水平管道内的总压头耗费在使液体流动（造成速度压头）和克服流体阻力上。这种情况可以从已知的公式得出：

式中 H——总压头（m）；

ΔH_v——消耗在速度上的压头损失（m）；

ΔH_T——克服管道摩擦的压头损失（m）；

ΔH_h——克服管道转弯，管接头、异径管等处阻力的压头损失（m）；

ΔH_f——克服阀门局部阻力的压头损失（m）。

众所周知，在管道内介质的流动有两种状态：层流和紊流。在第一种情况时，压头损失与管路中液体的平均流速成比例；在第二种情况下，压头损失与液体流速的平方成比例。

当Re_D＜Re_K时，产生层流；当Re_D＞Re_K时，产生紊流。式中Re_D——与管路直径有关的雷诺数；

Re_K——临界雷诺数（对于管道，通常取Re_K=2320），对于各种不同管道系统雷诺数临

界值是不同的，可达到2×10⁴或1×10⁵。

当Re_K≤10⁵时，必然要产生带有平方关系的ΔH=f（v²）紊流。

对于圆形截面管道：

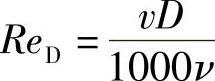
式中 v——管道内介质的流速（截面的平均流速）（m/s）；

D——管道内径（mm）；

ν——介质运动粘度（m²/s）。

介质的运动粘度也可以用斯托克斯（St）或者厘斯（cSt）来表示（1St=10^-4m²/s，1cSt=10^-6m²/s）。

介质的粘度还可用动力粘度η表示，其单位为泊（P）或者厘泊（cP），动力粘度η与运动粘度ν的关系为

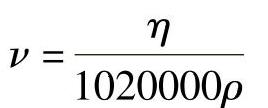
式中 η——动力粘度（Pa·s）；

ρ——介质密度（g/mm³）。

注：1P=0.1Pa·s；1cP=1×10^-3Pa·s。

介质通过阀门的压头损失一般可用下式表示：

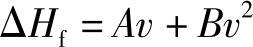
式中A、B——阀门一定开度下的常数。

若为粘性介质且流速很低时，第一项Av起决定性作用，在其他情况下；第二项Bv²起决定性作用。

在绝大多数情况下，管道内介质的流动呈紊流状态，Av值对压头损失影响不大，故可忽略不计。因此，在阀门计算时，可采用下述公式：

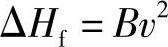
实验证实，此公式精确的表示形式为

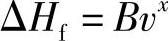
式中x=1.6～2.4。

由于目前还没有足够的数据说明阀门结构对指数x的影响，通常取x=2。

通过多种阀门的试验表明，在一般情况下，对于水可以取x=2。为了进行阀门的流体阻力计算，必须知道管道内介质的流速v，此流速可以通过流量来确定（即质量流量q_m或体积流量q_V）。

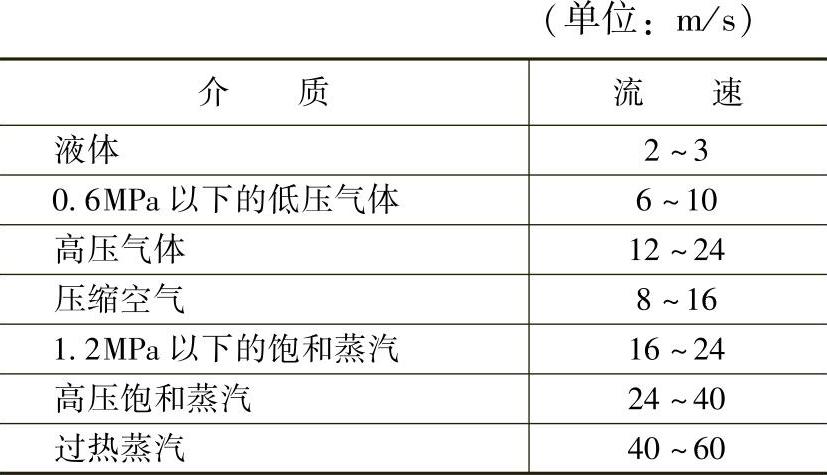
管道内输送介质通常采用表2-1的流速。

介质在管道内所选取的流速取决于技术与经济因素和具体使用条件。例如在火电站，由于蒸汽在高压下的密度很大，故高压蒸汽在管道内所选取的流速比低压蒸汽要低。

为了简化计算，在阀门流体阻力计算公式中采用下列计量单位：介质流速v，单位为m/s；液体或气体的密度ρ，单位为g/mm³；压力单位为MPa。

表2-1 管道内一般采用的流速

若流量规定用体积流量q_V（单位为m³/h），则流速v（单位为m/s），按式（2-2）计算：

式中A_N——管道横截面积，按公称尺寸计算（mm²）。

如果流量规定用质量流量q_m（单位为t/h），则流速v（单位为m/s），按式（2-3）计算：

式中 ρ——在给定条件下（即绝对压力为p，单位为MPa，温度为t，单位为℃时）液体或气体

的实际密度（g/mm³）。

如果介质是可压缩的气体，其密度按下式计算：

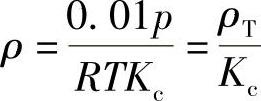
式中 ρ_T——在给定条件下，气体的理论密度（g/mm³），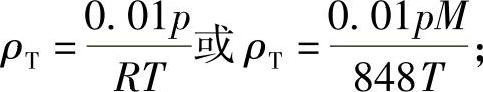

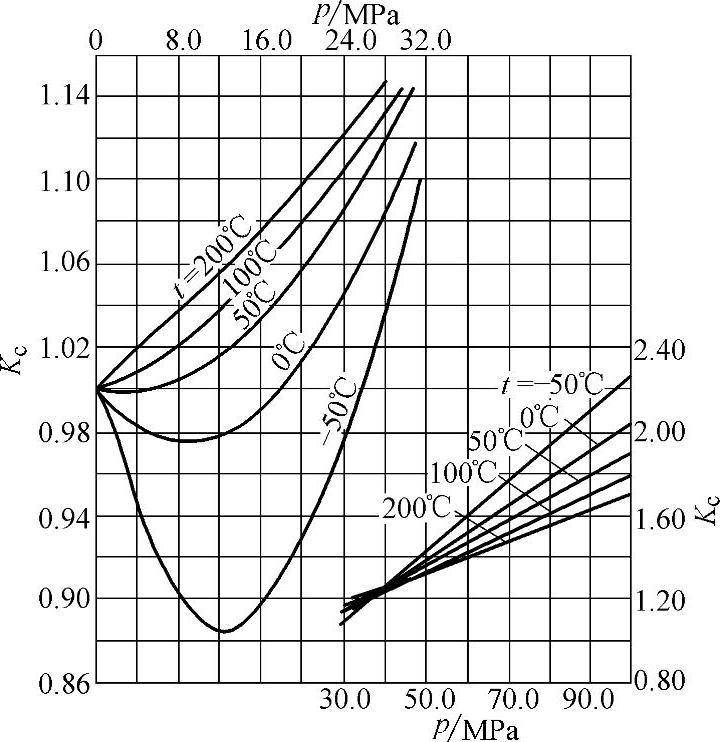
K_c——压缩系数，考虑实际密度与理论密度（按理想气体计算）间的误差，几种气体的K_c值可按图2-1～图2-10选取；

T——热力学温度（°K），T=273+t℃；

R——气体常数（kg·m/kg·K），；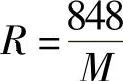

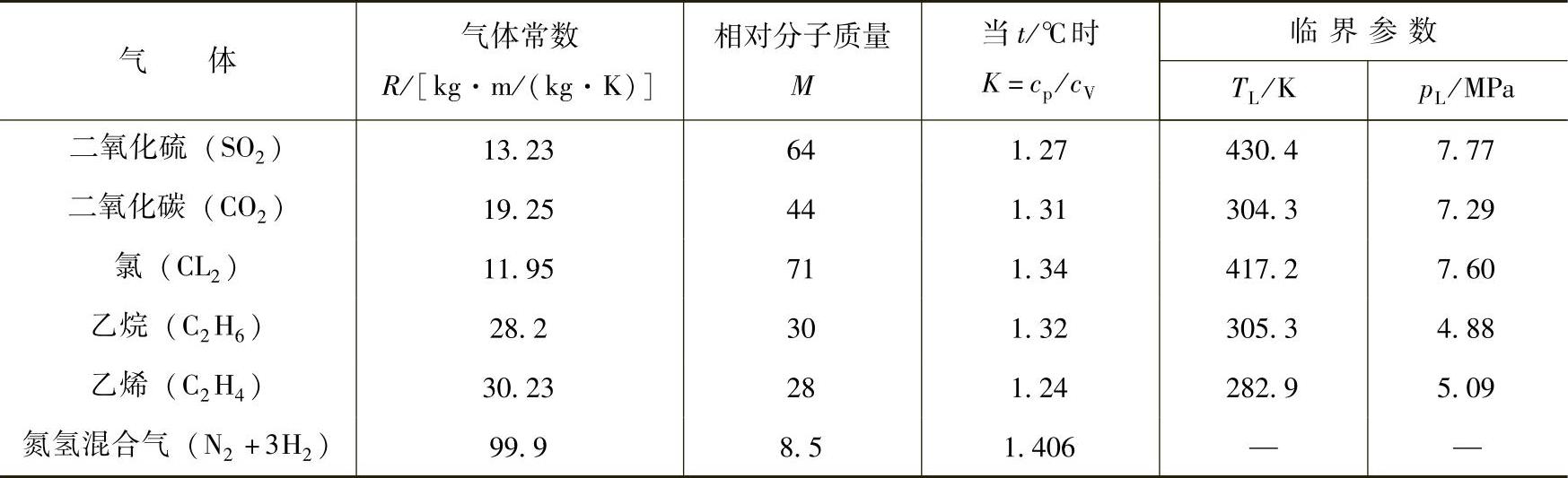
M——相对分子质量，按表2-2选取；

p——绝对压力（MPa）。

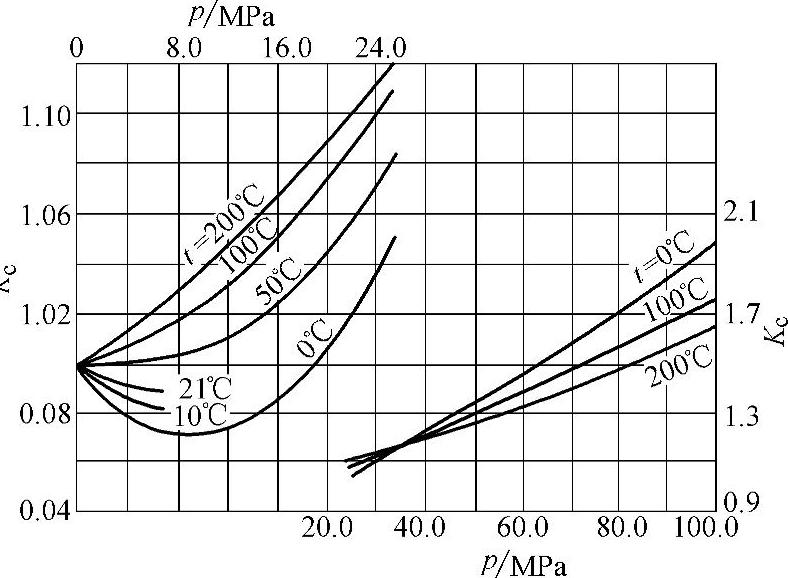
图2-1 空气的压缩系数K_c值

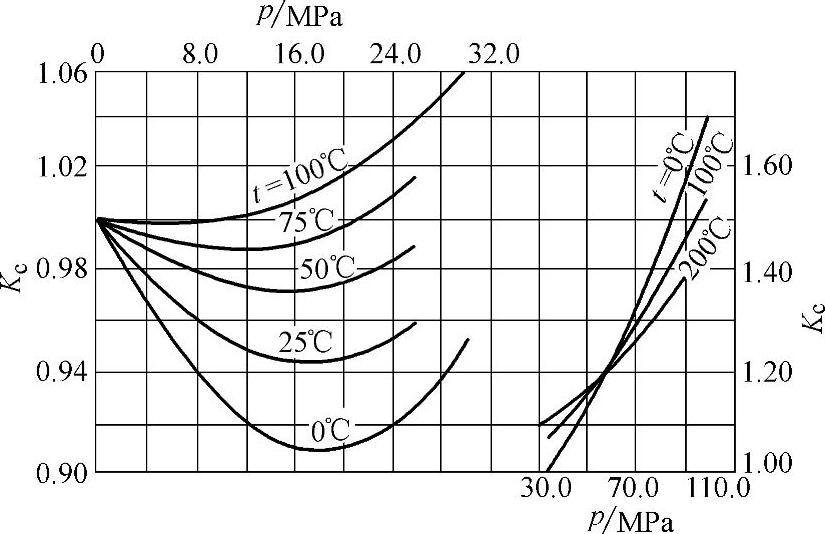
图2-2 氧气的压缩系数K_c值

图2-3 氢气的压缩系数K_c值

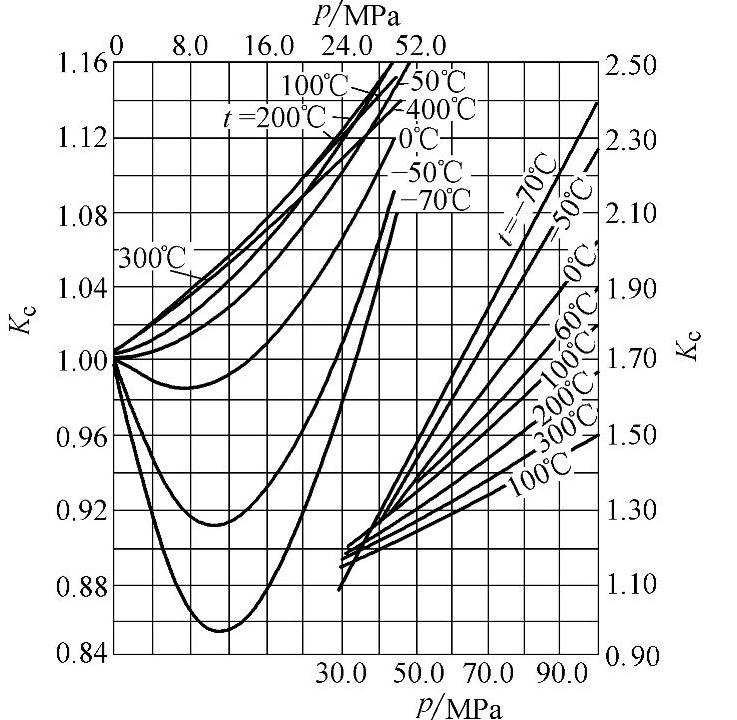
图2-4 氮气的压缩系数K_c值

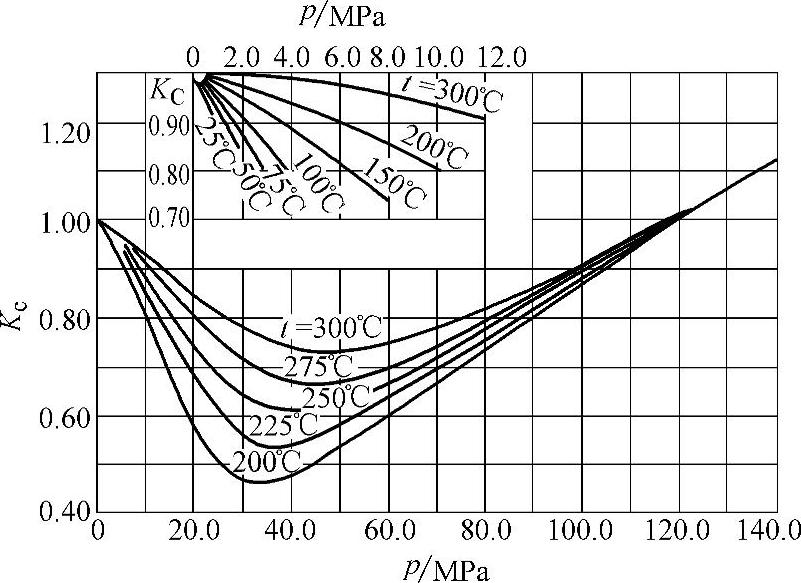
图2-5 氨气的压缩系数K_c值

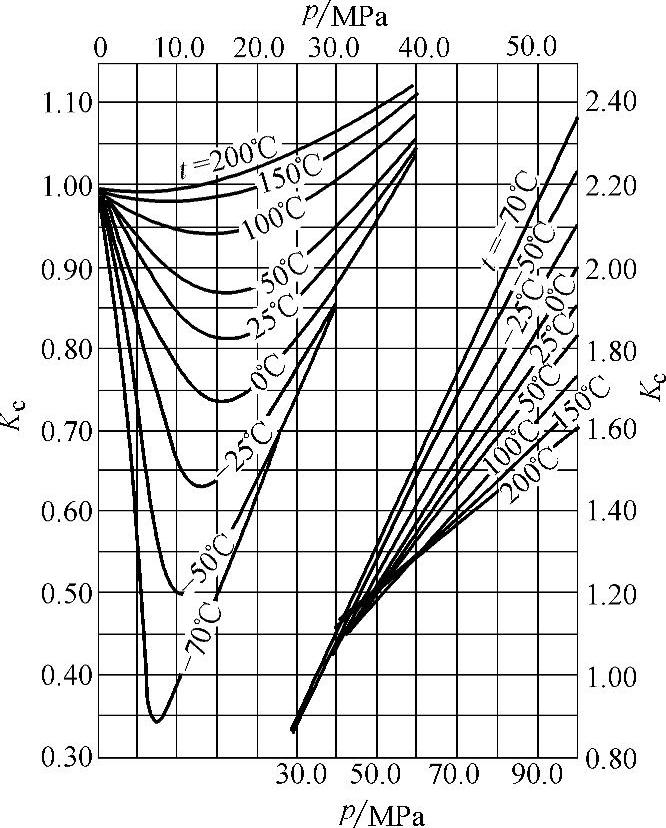
图2-6 甲烷的压缩系数K_c值

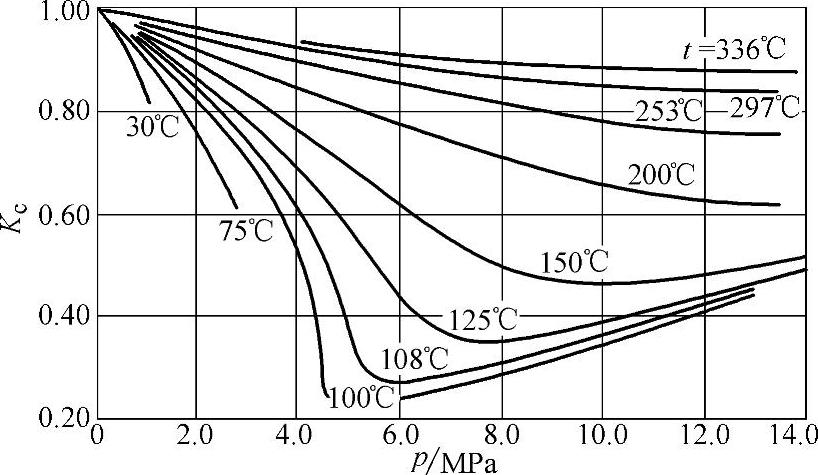
图2-7 丙烷的压缩系数K_c值

(www.xing528.com)

图2-8 一氧化碳的压缩系数K_c值

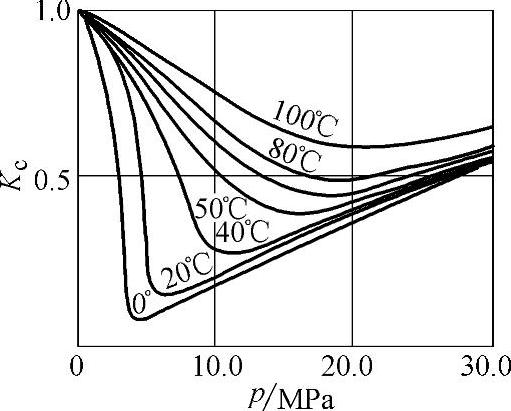
图2-9 二氧化碳的压缩系数K_c值

图2-10 水蒸气的压缩系数K_c值

表2-2 一些气体的基本参数

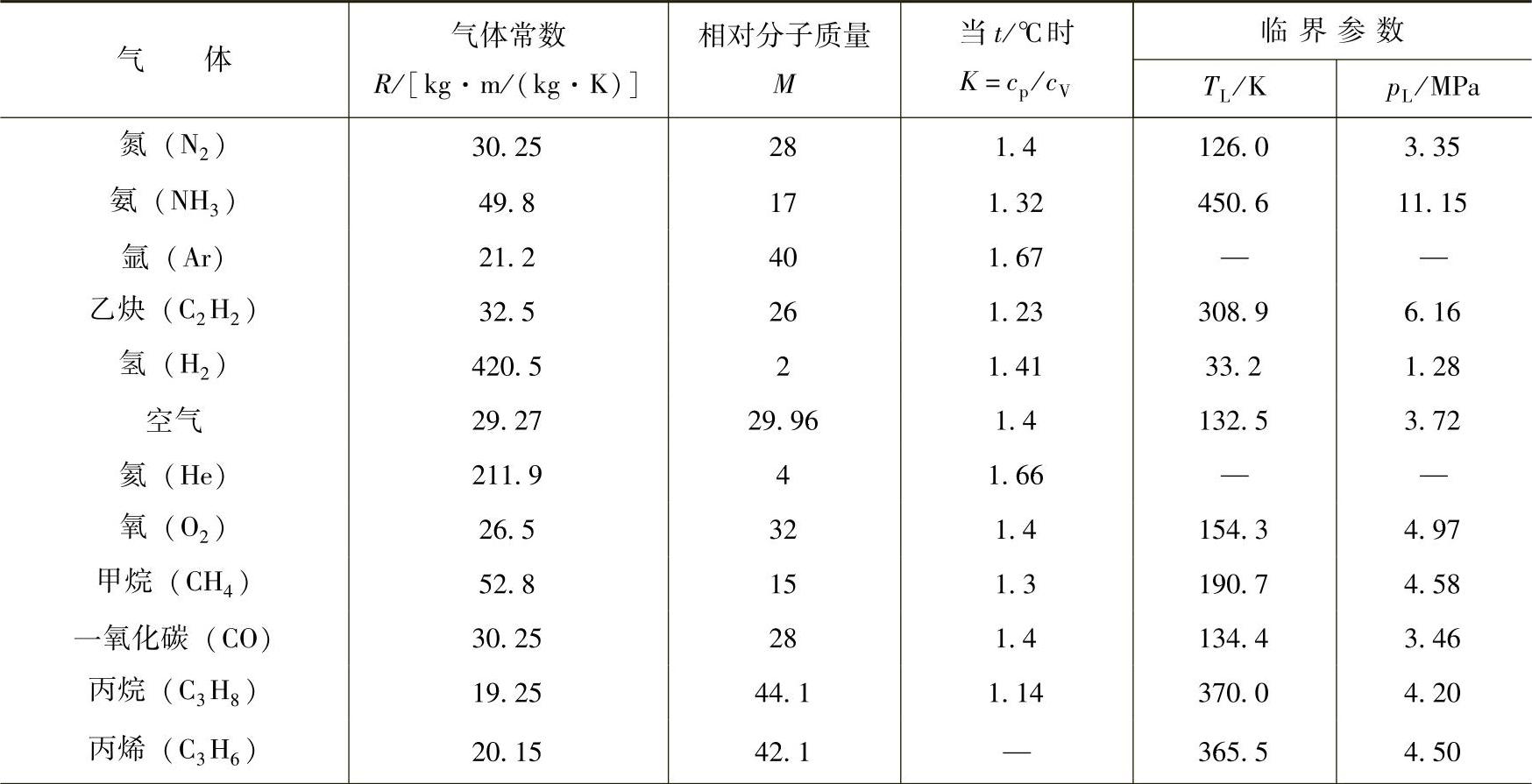
（续）

为了计算流经管路水蒸气的质量流量q_m（单位为t/h）或者确定其管道直径，可利用图2-11的诺模图。此图包含四个变数p、q_m、v和D，根据三个给定的参数确定第四个参数。

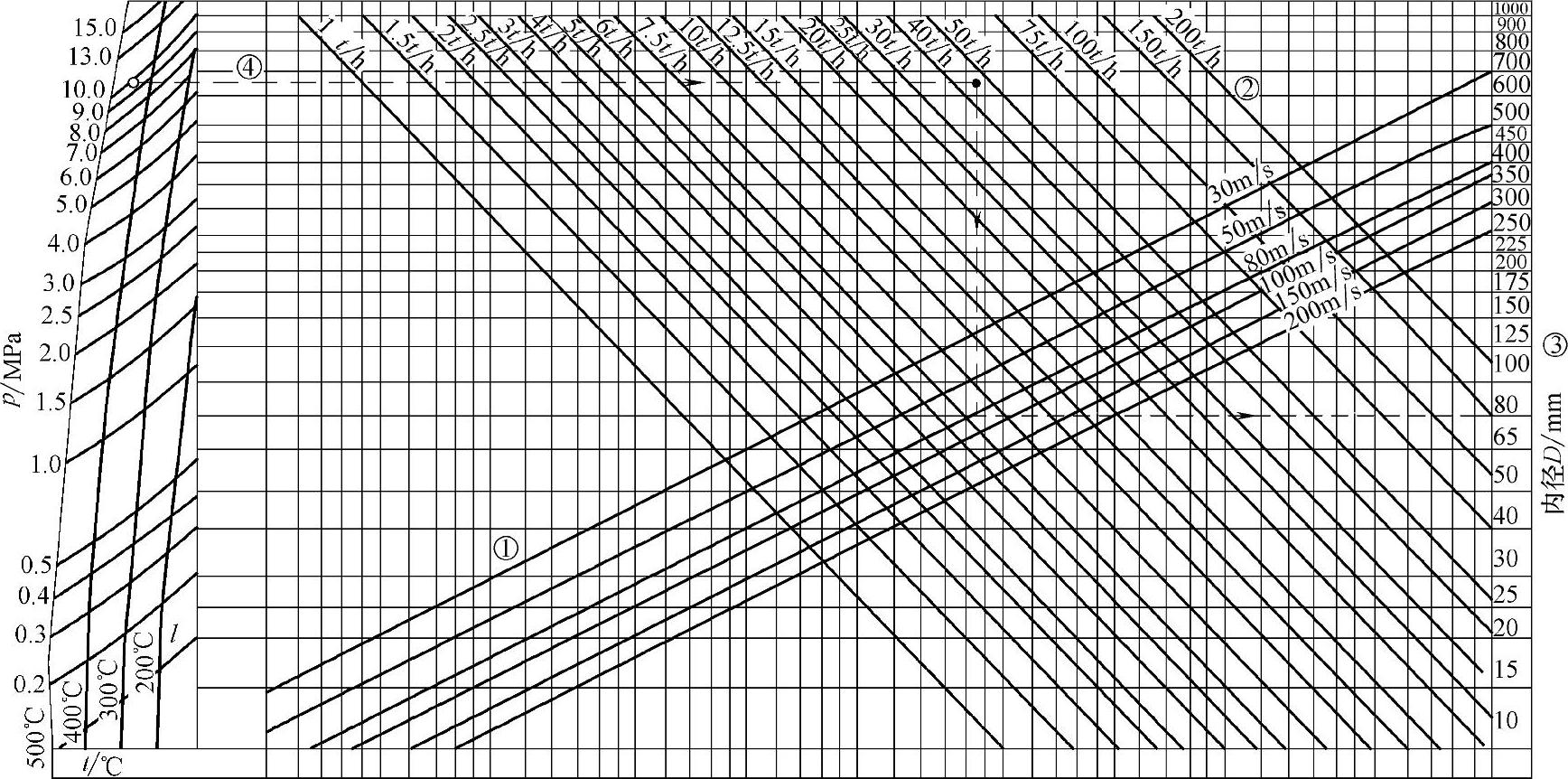
图2-11 确定管内蒸汽流量图（诺模图）

①蒸汽流速v/(m/s)

②流量q_m／(t/h)

③内径D/mm

④例P=lO.OMPa,t=450℃，q_m=50t/h，v=80m/s,D=80mm

闭路阀的压头损失可以用ΔH（单位为m），或Δp（单位为MPa）表示。它们之间的关系是：10m高的水柱产生一个大气压的压力，因此，对于水

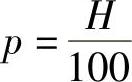
式中 p——压头H产生的压力（MPa）；

H——压头（m）。

对于密度为ρ的液体：

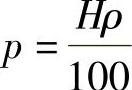
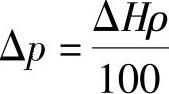
因此

则式（2-1）可改写成：

式中 p——压头H产生的压力（MPa）；

Δp_v——消耗在速度上的压力损失（MPa）；

Δp_T——克服管道摩擦的压力损失（MPa）；

Δp_h——克服管道转弯、管接头及异径管等阻力的压力损失（MPa）；

Δp_f——克服阀门局部阻力的压力损失（MPa），Δp_f=p₁-p₂，其中：p₁为阀前的压力（MPa）；p₂为阀后的压力（MPa）。

假定液体的全部位能转换成动能，则可得到理想液体在静压头H作用下的流动速度，其值能等于物体在这个高度的自由降落速度v（单位为m/s）：

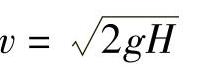
则

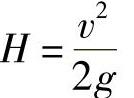
因此，式（2-4）中的各项可写成

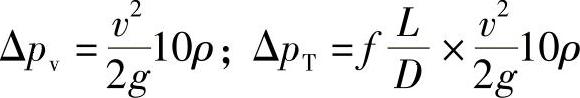
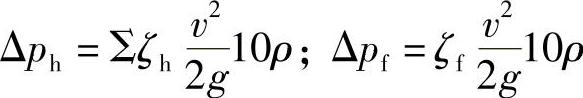
式中 ρ——介质的密度（g/mm³）；

g——重力加速度，g=9.81m/s²；

f——摩擦系数；

L——管道长度（m）；

D——管道公称尺寸（m）；

ζ_h——管道连接件的局部阻力系数；

ζ_f——阀门的局部阻力系数。

将上述公式代入式（2-4）得

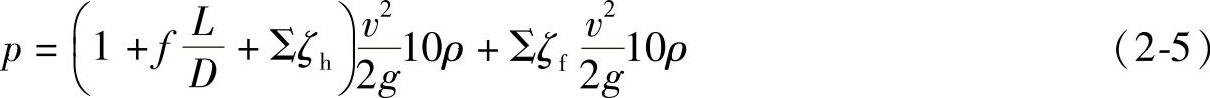
由此可见，在已知总压头的情况下，管道内介质的流速及流经管道的介质流量，将根据管道和安装在管道上的阀门的阻力而有所不同。

在管道阀门系统内，当总压头恒定时，阀门阻力的变化会改变介质的流量，而流量的改变却改变不了压头损失的总和，当重新进行稳定流速时，压头损失的总和仍旧不变。ζ_f值对流速变化的影响取决于管道系统的总阻力。

管道的阻力值使阀门设计计算复杂化，为了不受管道阻力值的影响，通常采用如下关系式：

因为以后只研究阀门，为了简便起见，只用Δp、ΔH、ζ，而不加下角注。

为了考虑附加因素对压头损失的影响，在式（2-6）中引入下列系数：

1）考虑到介质的可压缩性对压头损失的影响，对于气态介质，引入系数δ。

2）考虑到粘性介质对压力降Δp的影响，对于粘性介质和低流速介质引入系数ψ_p。

因此，得出以下通用公式：

当ζ值未知时，但阀座的开启截面积A_S（单位为mm²）及阀门在给定开启高度A_S/A_N下的总流量系数K_v为已知，则流阻系数ζ值可按下式确定：

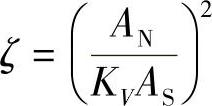
当ζ值未知时，而阀门的许用通过能力[K_V]为已知，其阻力系数可按下式确定：

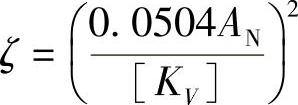
当介质流经阀门的流速未知时，其流速可按前面推导出的公式计算：

式中 q_m——液体的质量流量（t/h）；

q_V——液体的体积流量（m³/h）；

ρ——液体的密度（g/mm³）。

将求得的v及ζ值代入式（2-7）。

除特殊情况外，由液体粘度所引起的对压力降的影响可以忽略（ψ_p=1）。在输送粘性介质时，系数ψ_p可以根据雷诺数Re_D来确定。当Re_D≥1000时，ψ_p=1；当Re_D＜1000时，ψ_p值按图2-12曲线确定。