微电子封装的热机械可靠性设计相当耗费时间和金钱，现在的工业惯例是建立和组装原型系统，再对原型系统做大量的性能测试。虽然这种方法可能适合于“传统”的系统，然而当碰到一种新材料和新设计时，由于缺乏经验的指导，起初的几个原型一旦设计组装不当，将会出现失误。恢复实验原型系统再对其进行测试将要花好几个星期的时间，而每出现一次错误将损失大量的时间和金钱。因此，为了保证设计一次性成功，我们需要建立关于热机械可靠性设计的理论和方法。但电子封装组装工业界在相对较新的无铅钎料领域的设计经验较少，所以在从事耗时和耗钱的试验原型的建立和测试工作之前，很有必要进行热机械可靠性设计。
由于电子产品不断朝着微型化、高可靠性的方向发展，这使得焊点也向着更加微小的方向发展，焊点的应力应变情形又极为复杂，这无疑会给焊点的可靠性设计和分析带来了更大的风险，同时实验处理也会遇到很大的难题。数值模拟方法不但能简化这类复杂的问题，还可以节省大量计算时间。现实中很多工程问题是实验所无法解决的，如电子器件的尺寸等问题，但采用有限元模拟的方法可以使之优化。
无铅钎料合金种类繁多，美国国家电子制造促进会（NEMI）推荐使用在回流焊中使用Sn-3.9Ag-0.6Cu钎料，而日本电子信息技术产业协会（JEITA）则推荐使用Sn-3.0Ag-0.5Cu钎料。但大多数条件下，Sn-Ag-Cu（SAC）合金比Sn-Pb显现出更强的抗蠕变性，因而前者比后者蠕变要慢10～100倍。Sn-Ag-Cu钎料在微观结构、塑性、蠕变性能以及失效机理方面，与Pb-Sn相比有很大的不同。因此有必要为Sn-Ag-Cu钎料建立合适的热机械预测模型。
1.钎料本构模型
（1）Anand方程 有限元模拟中，设定钎料熔点为183～230℃左右，电子元器件的工作温度可能达到钎料熔点的一半左右，钎料可能会表现出粘塑性。有文献介绍当归一化温度高于0.5倍钎料熔点时，蠕变和应力松弛效果将非常明显。Sn-Ag-Cu钎料的熔点为217℃，室温下，温度已经达到熔点的0.61倍，出现明显的蠕变变形，Anand方程统一了蠕变和塑性引起的变形，可以较为准确地表现焊点的应力应变响应。使用粘塑性Anand方程来描述焊点的性能，即
内变量演化方程：
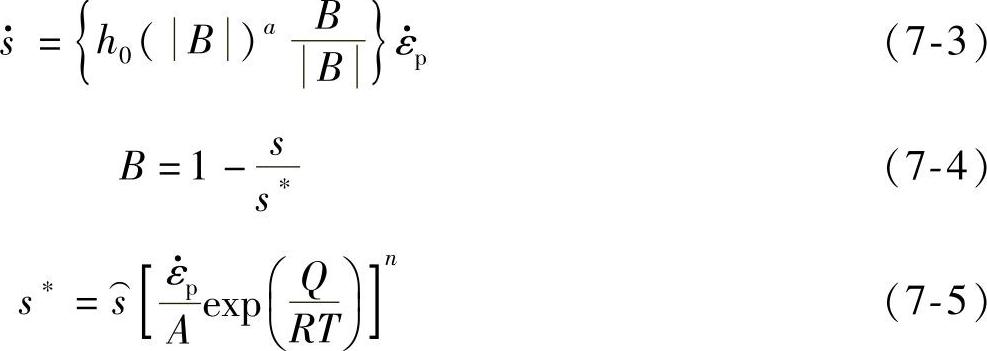
式中A——常数；
Q——激活能；
R——气体常数；
ξ——应力因子；
m——应变敏感指数；
s——系数；
n——指数；
h0——形变硬化软化常数；
a——应变指数。
目前国内外，使用该模型分析焊点可靠性的文献很多，通过模拟可以分析焊点的变形、最大应力应变和疲劳寿命。
（2）Garofalo-Arrheninus模型 大多数学者推荐采用Garofalo-Arrheninus模型来描述焊点的蠕变行为及应力应变响应，具体方程如下
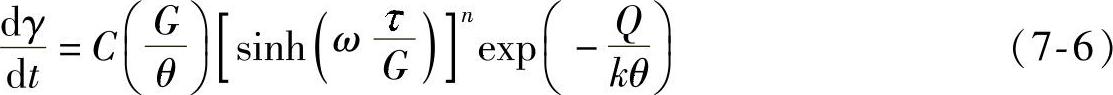
式中γ——切应变范围；
dγ——蠕变切应变速率；
dt
t——时间（s）；
C——材料常数；
G——和温度相关的剪切模量；
θ——绝对温度（K）；
ω——应力级别；
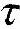——切应力；
n——应力指数；
Q——激活能。
Gonzales等人借助该模型运用Marc软件分析了倒装芯片器件焊点的可靠性，还比较Sn-Ag-Cu与SnPb共晶钎料在热循环载荷下的蠕变行为及疲劳寿命，结果发现，Sn-Ag-Cu焊点的疲劳寿命明显比SnPb焊点要高出27%～51%，这为无铅高密度组装提供了一定的理论依据。Sn-Ag-Cu-CNT为Sn-Ag-Cu基础上加入微量的碳纳米管材料，使之在熔点不变的气体下，提高材料力学性能，降低线胀系数，以便满足电子封装的需要，很多研究人员采用Garofalo-Arrheninus模型来分析这种钎料的蠕变性能。
（3）Norton模型 常用的还有Norton方程。假定材料的主要应变率由弹性应变和非弹性应变组成，即
式中ε·ij——总应变率张量；
ε·ijel——弹性应变率张量；
ε·ijcrp——蠕变应变率张量。
非弹性应变部分假设主要为稳态蠕变应变，描述的稳态蠕变模型可以用Norton方程来表示，方程如下：
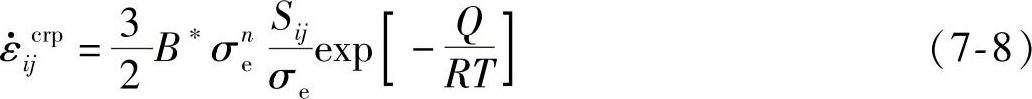
式中n——应力指数；
Q——激活能；
R——玻尔兹曼常数；
T——绝对温度；
B∗——材料常数；
σe——Mises应力，可以定义如下：
偏应力张量为
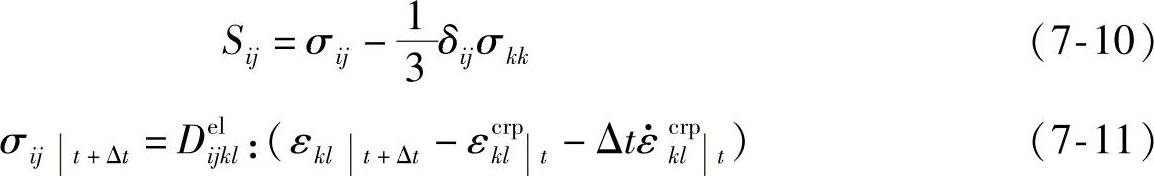
Gonzalez M.等人根据Garofalo-Arrheninus构建Sn-Pb和SnAg两种钎料的本构关系，用Norton方程来说明Sn-Ag-Cu的本构关系，通过比较三种钎料在热循环作用下的累积非弹性应变，并找出蠕变应变是焊点失效的主要原因。Zhang X. W.等人借用Norton方程构建63Sn37Pb钎料本构关系，分析了不同焊点形态及引线框架材料属性对焊点疲劳寿命的影响。
（4）Darveaux双曲模型 也可应用Darveaux双曲模型来描述稳态蠕变方程，即
式中α——应力系数；
Q——激活能；
A′、n——模型常数。
为了使计算方便，并且适合有限元软件分析的要求，Qi Y.等人把方程（7-12）简化成方程（7-13），这样只需测定C1、C2、C3、C4四个常数，就可以为模拟提供数据支持，并分析Sn-Ag-Cu与SnPb钎料焊点应力应变情况，即
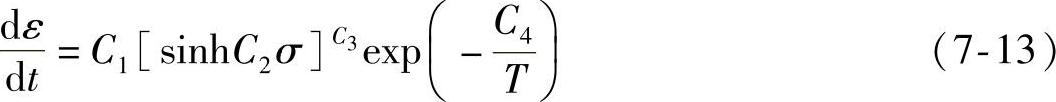
国内有关学者应用该模型描述了Sn-Ag-Cu钎料的本构关系，针对焊点的可靠性，研究了不同疲劳寿命预测方程的适用性。Kim、Pang、Vianco等诸多学者采用该双曲模型对无铅钎料的蠕变性能进行分析。Pang JHL和Chen FX通过构建Sn3.8Ag0.7Cu的双曲模型以及Anand模型，在接近焊点金属间化合物界面层分析焊点失效，运用两种模型得出的结果吻合。
（5）Wong模型 在模拟分析中，常用Dorn方程，ε·=Aσn模型进行分析，Norton模型就是根据Dorn模型演化而来的，Wong等人对Dorn方程做了修正，得出Wong模型，该模型也有广泛应用，即
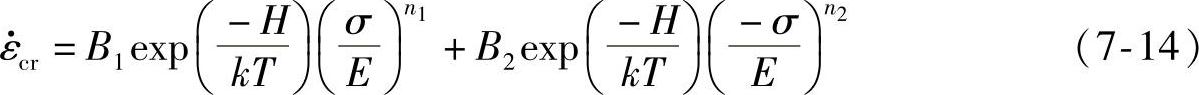
有关文献介绍，通过应用Wong模型，依据弹性、塑性和蠕变性能，在加载温度循环的情况下，分析Sn-Pb焊点内部应力—应变的响应。
（6）Wiese模型 Wises S.等人通过实验结果分析SnAg和Sn-Ag-Cu焊点本构方程，得到方程（7-15），第一项是相对应于低应力作用下对应的焊点蠕变速率，微观结构以位错攀移为主；第二项则是对应于高应力作用下的蠕变速率，微观状态以位错的滑移和攀移为主，即
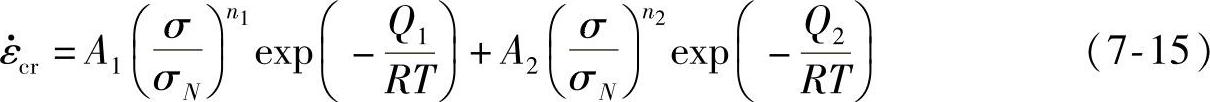
Stoechl等人采用Wiese模型和双曲正弦模型分析Sn4.0Ag0.5Cu钎料，用模拟软件分析不同模型下焊点的可靠性及疲劳寿命，结果表明两种模型模拟的结果相符，并和实验取得的结果一致。
2.疲劳寿命预测模型
（1）Manson-coffin疲劳模型及其演化方程Manson-coffin是常用来预测金属材料低周期疲劳失效的经典经验公式，形式为
式中Nf——热疲劳失效的平均寿命；
Δεp——循环塑性应变范围；
β、C——经验常数。
Engelmaier对上述模型进行了修正，综合考虑了频率与温度的效应，得到方程为(www.xing528.com)
式中ε′f——疲劳延性系数；
Nf——平均失效循环次数；
Δγ——切应变范围；
C——疲劳延性指数，即
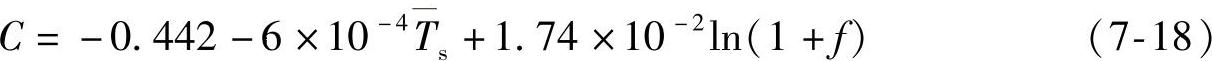
式中Ts——焊点平均温度；
f——循环频率；
1≤f≤1000——每天的循环次数。
（2）单一蠕变疲劳寿命模型Shine和Fox等人构建了蠕变应变为基础的疲劳寿命预测方程，其具体方程如下：
式中Nf——焊点失效循环次数；
Δγmc——单一循环蠕变应变；
C——与钎料结构相关的材料常数。
该模型中蠕变是由晶界滑移或基体位错引起的。
（3）综合塑性变形和蠕变的疲劳寿命预测方程Manson-coffin模型依据塑性应变来计算焊点疲劳寿命，但没有考虑到蠕变对焊点疲劳寿命的影响，Hossain等人对疲劳寿命方程作进一步修改，具体方程为：
以Von Mises等效塑性应变为基础循环次数，即
以累积塑性应变为基础循环次数：
以Von Mises蠕变为基础循环次数：
综合方程Von Mises等效塑性应变与Von Mises蠕变疲劳寿命，或综合累积塑性应变Von Mises蠕变疲劳寿命，构建出寿命计算方程分别为
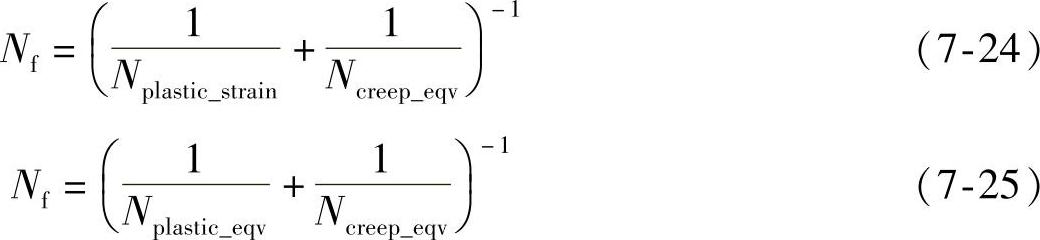
（4）基于蠕变和应变能密度的疲劳寿命预测模型 累积蠕变应变与基于累积蠕变应变能密度的疲劳寿命现在被广泛应用，该模型由美国Amkor公司的Syed提出。是以蠕变变形来进行寿命的预测为主，Syed认为，如果重复加载循环载荷，会发生蠕变现象，根据循环加载而产生累计蠕变应变，其对应寿命预测方程可以简化为式（7-26）：
Nf=（C′εacc）-1 （7-26）
式中Nf——焊点失效的循环次数；
εacc——累积的蠕变应变量；
C′=1/εf，εf——蠕变延性常数。
方程（7-27）为以累计蠕变应变能表示的焊点寿命方程，即
Nf=（W′ωacc）-1 （7-27）
式中Nf——焊点失效的循环次数；
W′——失效时的蠕变应变能密度；
ωacc——每一循环累计的蠕变应变能密度。
方程（7-26）、（7-27）为发生单一蠕变机制时蠕变寿命疲劳预测方程，但对两种蠕变机制均发生时，寿命预测方程会发生变化，即
式中CⅠ、CⅡ——蠕变应变模型常数；
WⅠ、WⅡ——蠕变应变能密度模型常数。
3.元器件模型建立与焊点可靠性分析
由于微电子焊接中的元器件种类很多，本文中选取常用的QFP、CSP、BGA等元器件的有限元模型来进行分析。焊点在微组装中十分微小，既承担机械连接的作用，也承担着电气连接作用。因而焊点的可靠性至关重要。焊点可靠性的影响因素有温度、潮气、振动和灰尘等。据美国空军电子工业部门的统计，电子元器件失效的原因有55%是由于温度变化引起的，20%是由于振动导致的，还有19%是由于潮气作用，另外6%是因为灰尘的原因引起的。四个影响因素中，温度对焊点的影响最大。当在热循环作用下，电子元器件材料与印制电路板材料之间存在线胀系数失配，在焊点中引起周期性的交变应力，长时间作用下将使焊点发生疲劳破坏，会使元器件发生失效。
（1）四边扁平引脚封装（QFP）元器件模型的构建和结果分析 QFP有着高密度、高可靠性以及优良的电气性能等优点，在大规模集成电路中具有普遍的应用，因此对QFP元器件的有限元模拟有重要的意义。图7-3为研究者利用软件模拟的QFP元件封装的有限元网格模型，其中图7-3a为二维模型，由于焊点是影响元器件可靠性的主要因素，为得到精确的计算结果，作者把焊点的拐角部分作精细划分。图7-3b模型则是为了简化计算过程，应用条状单引线模型来计算。QFP的四分之一的有限元模型如图7-3c所示，根据QFP元器件的对称性，取其四分之一来建模。由陶瓷载体、Cu引线、PCB板以及焊点组成模型。并定义焊点材料为非线性，其他材料定义为线性。应用该模型可以计算出在拐角处的应力最大，出现破坏的可能性也最大。对模型加载25～125℃的循环载荷。采用Coffin-Manson方程进行疲劳寿命预测，结果表明焊点的失效循环次数为213次，再通过温度循环实验验证，将最终得到焊点的疲劳寿命为186次。经过186次的热循环后，得到焊点的断裂形式为完全脆性断裂方式，这说明理论值和实验值较一致。
图7-3 QFP元件的有限元网格模型
a）二维模型 b）三维单引线模型 c）四分之一模型
（2）片式电阻模型的建立及结果分析 通常片式电阻也是常见的表面组装元器件，Stephen等人利用PHYSICA有限元软件构建型号为2512电阻的四分之一网格模型，模型如图7-4所示。使用弯曲和拉伸实验来分析焊点出现裂纹的情况。得到焊点的裂纹发生区域如图7-5所示，并且分析了裂纹扩展的三个不同方向，最后比较裂纹发生的长度。
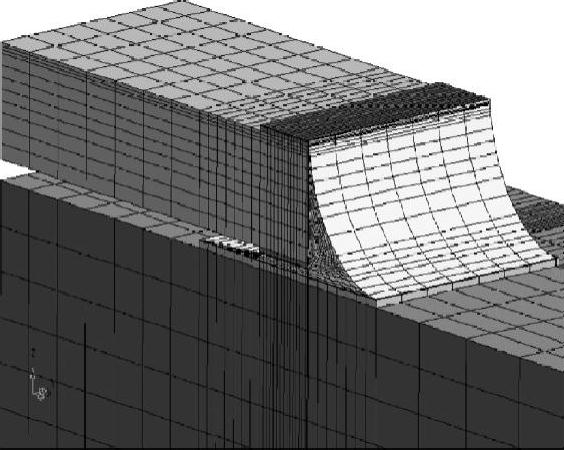
图7-4 片式电阻有限元模型
图7-5 焊点裂纹发生云图
（3）BGA和CSP模型的建立及结果分析 对CBGA封装形式，人们认为焊点模型的建立如果越接近真实形态，计算的将越精确。然而Andy Perkins等人运用ANSYS有限元分析软件一反常态地采用柱状焊点来替代球状焊点，能精确地计算出焊点的疲劳寿命，陶瓷球栅阵列的四分之一有限元模型如图7-6所示。采用柱状焊点取代球状焊点，能将焊点阵列对角线拐角处的焊点网格进行精细划分，对其余部位焊点网格粗划，也能得到精确的计算结果，该法已在相关的实验和模拟中得到证实。图7-7为PBGA器件的条状有限元模型，使用单一条状模型可以简化计算量，根据该模型，基于蠕变模型可有效地分析温度载荷参数对Sn-Ag-Cu无铅焊点的可靠性影响。
图7-6 CBGA四分之一有限元模型
通过有限元分析，研究钎料焊点的力学性能，进而挑选出力学性能好、可靠性能高的钎料。Lau、Drveaux等人用构建钎料的蠕变速率方程，得到了Sn-Pb和Sn-Ag-Cu两种钎料在一致温度下蠕变速率与Von-Mises应力曲线，发现在相同温度和蠕变速率下，Sn-Ag-Cu钎料的力学性能要优于Sn-Pb钎料，与此同时，Bart Vandevelde等人依据Drveaux等人的钎料蠕变速率方程来构建5×4CSP封装的四分之一模型，通过对其施加热循环应力进行模拟。对应的有限元模型见图7-8a，图7-8b是Sn-Ag-Cu焊点在两个热循环后球形焊点的应力云图。从图7-8b中明显可以看出拐角焊点的非弹性应变达到峰值。
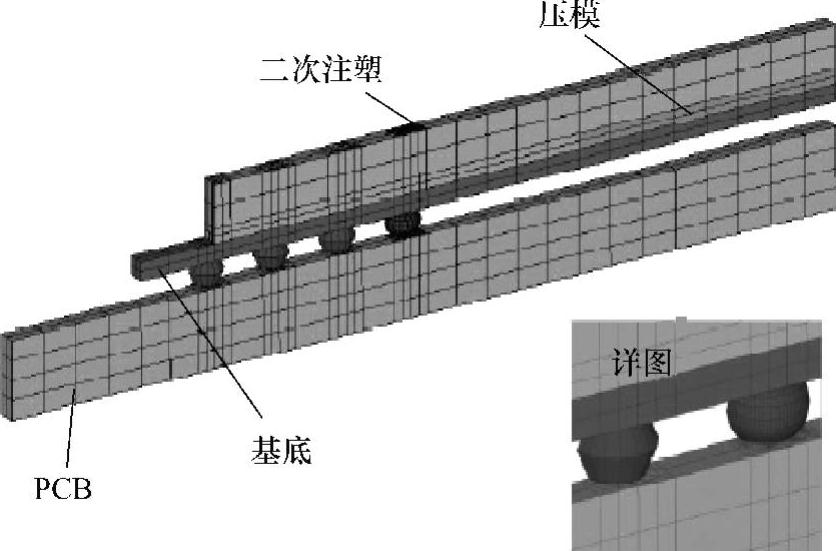
图7-7 PBGA器件的条状有限元模型
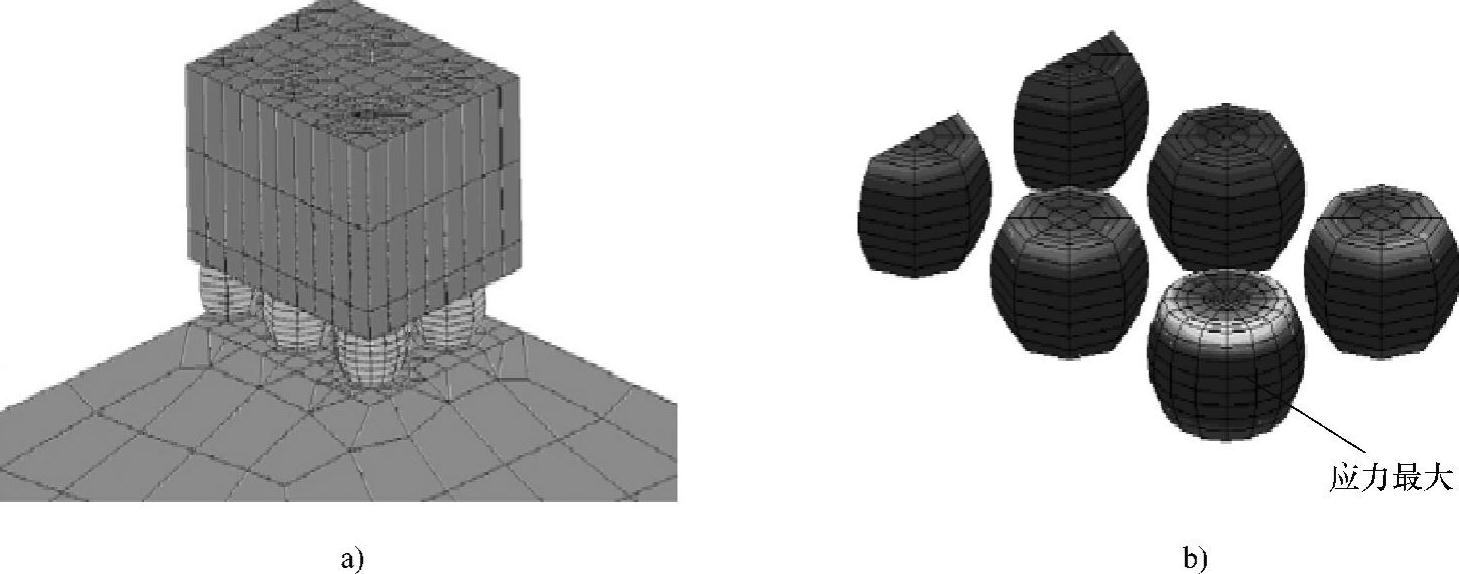
图7-8 CSP有限元模型
a）CSP有限元模型 b）焊点的应力云图
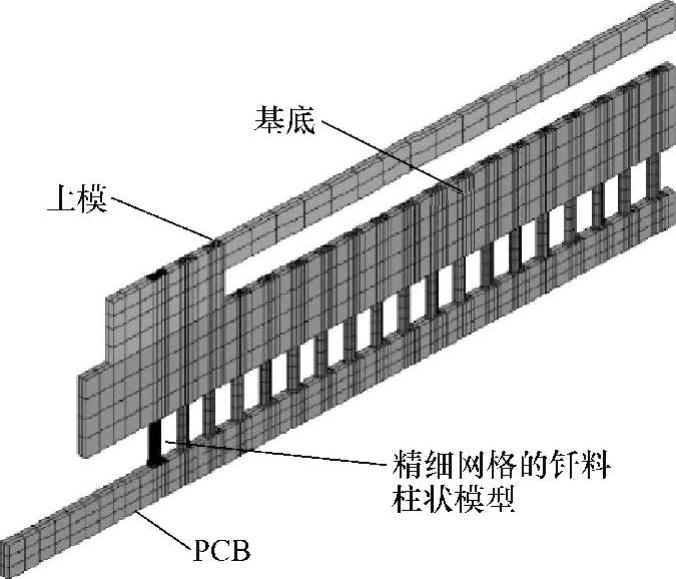
图7-9 条状CCGA有限元模型
（4）陶瓷柱栅阵列（CCGA）元器件模型的建立及应用 目前对球栅阵列数值模拟的研究已非常普遍，但柱状焊点的研究相对较少，CCGA适用于高I/O接口的芯片组装形式，该封装形式具有的高频率、易散热被IBM推荐为封装的最佳形式。John Law等人借助ANSYS软件构建了1657CCGA元器件的条状有限元模型，从图7-9可以看出，通过比较三种不同热循环条件下，95.5Sn3.9Ag0.6Cu与63Sn37Pb两种钎料的蠕变性能，结果显示95.5Sn3.9Ag0.6Cu对应焊点的应力应变大于63Sn37Pb对应焊点的应力应变，且95.5Sn3.9Ag0.6Cu对应焊点的疲劳寿命相对较小。
（5）FCBGA焊点可靠性分析 通过有限元模拟能够预测焊点裂纹的发生位置，Spraul等人运用Surface evolver和ANSYS两种软件对倒装球栅阵列焊点的失效模式分析，如图7-10a所示。结果表明蠕变最大的地方为裂纹的发生位置在靠近金属间化合物的位置，在实验中得到了有效的验证，实验失效焊点如图7-10b所示，模拟计算结果和试验结果相符，另有文献基于Anand方程模拟的结果与Spraul等人的结果相似，这为有限元的应用提供了合理的理论依据。
图7-10 FCBGA焊点蠕变图
a）焊点蠕变云图 b）经过热循环的失效焊点
另有研究人员对通孔插装元件做了详细的研究，使用Evolver输出表面形态，研究焊点在回流焊作用下的热疲劳性能，结合Marc7.0进行有限元分析，得到其等效蠕变图，图7-11表明应力集中在钎料和镀铜管处，同时也说明该处容易引起裂纹并扩展。
图7-11 插装再流焊焊点等效蠕变图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
