自动判别高差阈值的移动曲面滤波方法

1. 基于多回波数据的高差阈值自动选择

根据本小节分析，多回波信息主要记录了树木的激光反射特性。多回波信息的末次回波激光脚点往往是位于地面点，而首次回波和中间次回波的激光脚点则是位于树木。位于树木附近的单次回波激光脚点可以按照其高程进行判别，当其高程明显高于树木最高次回波的高程时，该激光脚点更有可能是位于人工建筑物点，而当某激光脚点明显低于末次回波激光脚点的高程时，该点更有可能是地面点。通过以上分析，我们选择某一多回波数据八邻域内高程值较低的激光脚点作为地面点，然后建立一个类似于地型表面的平面，计算多回波数据中每次回波的激光脚点到该平面的高程差，最后进行统计分析，筛选出后续滤波的高差阈值。

阈值自动选择算法设计：

①首先对点云数据进行数据组织。虚拟格网的建立依据规则格网建立准则，但不用对数据进行内插，按照点云数据的平面坐标进行建立格网索引。

②对格网内数据进行遍历。当点云数据中回波次数(Return Number)n 大于1 时，该激光脚点数据为多回波数据，将同一束激光的回波信号分配到同一检索号。遍历完所有数据后，按照高程小于多次回波数据的首次回波数据的高程值的原则，在该数据所在的格网内搜索单次回波的激光脚点数据，当格网内没有足够数量(至少三个)符合条件的单次回波数据时，舍弃该多回波数据。

③当格网内的某一多回波数据的单次数据量满足要求时，选择高程数据最低的三个单次回波激光脚点数据作为建立类似地形表面的平面三角形。假设三个脚点数据分别为：Ga(xa，ya，za)、Gb(xb，yb，zb)和Gc(xc，yc，zc)，多回波数据为P，多回波数据中每个回波的激光脚点为Pi(xi，yi，zi)，则与该多回波数据相关的平面方程为：

④根据空间数学，计算多回波数据中每个各回波激光脚点到相关平面的距离d 为：

⑤按上述步骤，遍历完测区所有的数据，将计算所得的高差值按照回波次数进行分类，即首次回波激光脚点的高程差值集合、中间次回波高程差值集合以及尾次回波高程差值集合。对每组数据进行分析，通常来讲，这些高程差值都会在一定的范围之内，当高程差值过大或过小时，说明该数据有异常，可以剔除。根据数学分析，得到各回波次数的距离分布情况。

⑥选择合适的距离d 作为后续算法的高程阈值。通过分析多回波数据的各回波激光脚点的对应位置，我们可以发现绝大部分末次回波激光脚点都位于地面，只有极少部分是非地面点。因此，在剔除异常的值后，选择末次回波数据的最大距离差值作为高差阈值。当待定点的高程插值大于末次回波高程插值的最大值时，认为点为地物点；反之，则认为该点为地面点。

表11-6 是多回波数据(来自实验区一)高差的计算结果，剔除异常值之后，首次回波的高差范围为10.8～20.6m，中间次回波的高差范围为2.5～11.6m，而末次回波的高差最大值为1.85m。按照阈值选择准则，我们取高差阈值为1.85m，作为区分地物点和地面点的高差。

图11-12 中红色表示同一束激光的多次返回激光脚点数据，蓝色点为单次回波数据。

表11-6　点云数据高差阈值计算结果(马云栋，2015)

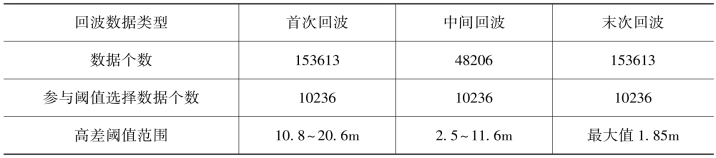
图11-12　多回波数据激光脚点落点示意图

2. 改进移动曲面拟合滤波方法

按照本书11.2 节讨论的移动曲面拟合滤波方法，本节在阈值的选择上做了改进，改进后的滤波方法如下：

①滤波高差阈值的自动判别，按照上节中提出的高差阈值自动判别算法，选取适合该数据区域的高差阈值。

②按照本书11.4.1 中提出的点云数据分类方法，将多回波数据中的首次回波和中间次回波激光脚点数据滤除，只留下末次回波数据参与后续滤波。将得到的新的点云数据进行二维排序。

③选取种子区域进行滤波。选取种子区域内相邻的最低的三个点作为原始地面点，并得到一个初始拟合面。然后把相邻备选点的平面坐标带入到平面方程中进行计算，得到备选点的拟合高程。将备选点拟合高程与观测高程做差，得到备选点的高差值。如果高程差在阈值之内，则认为该点为地面点并接受，反之就将其作为非地面点滤掉。

④当备选点被接受成为地面点时，把最原始的地面点脚点踢出，再把剩余两点与新入选点确定一个新的平面，不断重复该过程。当遍历完整个测区后，就完成了滤波过程。

下面将通过实验验证改进后的移动曲面拟合滤波方法的可行性和适用性。

3. 实验验证

本节实验分为两部分，实验一为验证对比实验，主要将算法应用于有一定地形起伏的山区，并与移动曲面拟合算法的滤波效果作对比，来研究本书提出的算法的精度。实验二的设置是为探究算法的适用性，测试区域为城镇区域，地形起伏较小，多为房屋等人工建筑，并有一定的植被覆盖。

(1)研究区概述

实验区一：从http：/ /lidar.asu.edu/data.html 下载，位于福蒙特州。该区域大部分被森林覆盖，地形有一定起伏。点云数据密度为0.944 点/平方米。高程最低点为130.32m，高程最高点为258.21m，最大回波次数为4 次。

实验区二：某一城镇，数据总数为627458 个，数据回波信息如图11-13 所示。

图11-13　实验区二数据回波信息

(2)实验环境(www.xing528.com)

①硬件设备：ThinkStation 工作站。

②操作系统：Microsoft Windows7。

③开发平台：C。

(3)实验流程

实验一：

滤波高差阈值自动选择。根据表11-9 中得到的结果，选取1.85m 作为本次实验的高差阈值。

参与滤波算法数据选择。根据作者提出的分类方法对数据进行分类，最后得到参与数据滤波的尾次回波激光脚点个数为475472，为原始数据的70%左右。

种子点选取，尾次回波数据的激光脚点按高程大小排序，选择高程最小点作为种子点，并选取相邻合适的点作为初始三角形的节点。然后对待定点进行判定，待遍历完所有数据后，结束滤波。

本章还利用移动曲面拟合法对原始点云数据进行处理，用在对比滤波效果和效率上。

图11-14(a)是实验区域的遥感图像，图11-14(b)是实验区的DSM，图11-14(c)是滤波后的点云显示，其中绿色为地物点，黄色为地面点。从图11-14 中可以看出，本滤波算法能够滤除绝大部分的地物点，但仍有少量的低矮植被点被保留下来。红色框内标记的区域分别为公路附近的植被和建筑物，在图11-14(c)中可以看出，这两种地物的激光脚点数据都被滤掉。

图11-14　地面点和地物点分离结果(马云栋，2015)

在图11-15(a)为本章算法滤波后利用地面点建立的DEM，图11-15(b)是移动曲面拟合法得到的DEM，图11-15(c)是利用ENVI 软件处理后的DEM。从图中方框区域可以看出，本章提出的滤波算法能够很好地保留地形，保证了地形的连续性；在移动曲面拟合算法建立的DEM 中，红色方框内出现尖刺现象，这说明滤波过程中少量一些地物点被保留下来；而绿色方框内的地形太过于平坦，不符合当地的实际情况，则说明该区域内的一些地面点被滤掉，滤波效果不佳。与ENVI 处理的效果相比，绿色方框内，ENVI 处理后的DEM 地形起伏较小，而本章提出的滤波算法则较好地呈现了地形起伏，在地形表现上更好。

图11-15　滤波后DEM

综上所述，本章提出的滤波算法能够较好地分离地面点和地物点。与通过移动曲面拟合方法所得到的DEM 作对比，我们可以发现本章提出的滤波算法能够很好地保留森林地区的地形信息，而且能够有效地减少将地物点误分为地面点的概率，即减少第Ⅰ类误差。

实验二：

滤波高差阈值自动选择。选取1.4m 作为本次实验的高差阈值，计算结果如表11-7所示。

表11-7　点云数据高差阈值计算结果

参与滤波算法数据选择。参与数据滤波的尾次回波激光脚点个数为5936306 个，由于该数据为城区，多回波数据点占总体数据的比例不高，所以参与滤波的数据占总体数据的95%。

种子点选取，尾次回波数据的激光脚点按高程大小排序，选择高程最小点作为种子点，并选取相邻合适的点作为初始三角形的节点。

对待定点进行判定，待遍历完所有数据后，结束滤波。

本章还利用数学形态学法对原始点云数据进行处理，用在对比滤波效果上。

图11-16(c)为本章提出的滤波算法运算后的地面点显示，图11-16(d)为数学形态法后的地面点显示。对比原始点云数据和DSM，可知图11-16(d)方框内的激光脚点大多位于房屋和树木，图11-16(c)中这些激光脚点已经被滤除，说明本章提出的滤波算法的效果要优于数学形态学滤波算法。

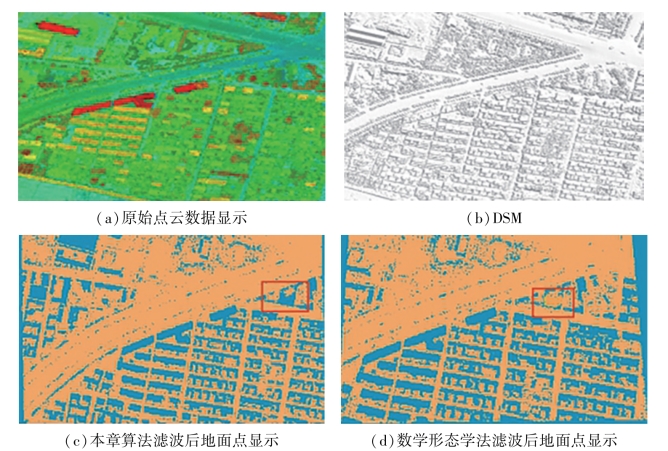
图11-16　滤波后结果对比图

图11-17(a)为DSM，图11-17(b)为本章滤波算法得到的DEM，图11-17(c)为数学形态学滤波后建立的DEM。红色框内为建筑物及少量树木，绿色框内为路边行树。通过对比图11-17(a)和图11-17(b)，可以看出，本章滤波算法能够有效地应用于城市区域，可以很好地剔除树木点和建筑物点。对比图11-17(b)和图11-17(c)，相对于传统数学形态学滤波算法，本章提出的滤波算法能很好地将树木点和建筑物点剔除，而且能有效地提高滤波精度，减少将地物点误分为地面点的概率，即减少第Ⅰ类误差。

图11-17　滤波后DEM 与滤波前数据DSM 对比(马云栋，2015)

4. 实验结果分析

通过对比实验，验证了本章所提出的算法的可行性，而且该算法不仅能够应用于森林地区，还能够应用城镇区域。通过实验结果比对，本节所提出的滤波算法能够有效地降低第Ⅰ类误差，而且也能够很好地保留地形特征。总体上来说，本节所提出的算法具有很高的可行性和适用性。