离子注入的基本原理

1.射程分布理论（LSS理论）

射程分布理论（LSS理论）由J.Lindhard，M.Scharff和E.Schiott提出，用于研究低速度重离子在无定形靶材中的射程分布。LSS理论所得出的结论可适用于质量范围相当宽的入射离子领域。

当一束带电粒子轰击靶材时，轰击离子和靶材表面原子（原子团）相互作用，同时伴随能量交换。一种情况是轰击离子与靶材表面原子碰撞后反射离开；另一种是轰击离子射入靶材内。这部分离子可称为入射离子（注入离子）。如图7-14所示带有一定能量的入射离子在靶材内同靶原子核和电子（束缚电子和自由电子）相碰撞，进行能量交换，入射离子损失能量，最终停留在靶内某一位置。入射离子从靶材表面到停止期间所走过的总距离称为射程R，这一距离在入射方向上的投影称为投影射程RP，这一距离在垂直入射方向上的投影可称为横向偏移RT（见图7-15）。

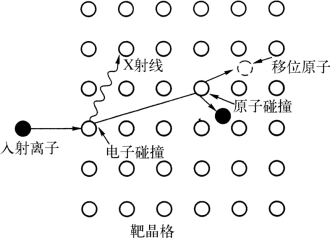
图7-14　入射离子与靶原子的碰撞

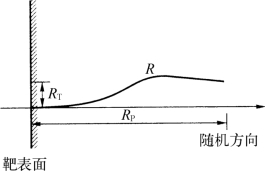
图7-15　总射程R，投影射程RP和横向位移RT

入射离子在靶内的能量损失过程包括两个独立的部分，入射离子与靶原子核作用而产生的能量损失和入射离子与电子作用而导致的能量损失。因此对于单个入射离子来讲，单位距离上的能量损失可表示为这两部分之和。

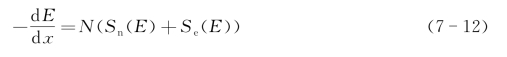
式中，E是入射离子在靶内x点的能量，Sn（E）是原子核阻止能力，表示能量为E的一个入射离子在单位密度的靶内通过dx厚度传递给靶原子的能量；Se（E）是电子阻止能力，表示能量为E的入射离子在单位密度的靶内通过dx距离传递给靶内电子的能量；N为单位体积内靶原子的平均数。

当Sn（E）和Se（E）可知时，一颗入射离子由初始能量E1到停止时在靶内所走过的总距离R就可积分求得：

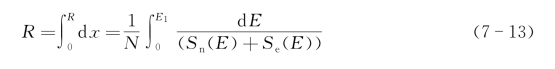
在这一计算过程中入射离子的能量损失是作为连续过程来处理的，此时得出的距离R称为平均总射程，对于简单地估算入射离子在非晶材料内的入射深度是有用的。

2.Sn（E）和Se（E）的计算

Sn（E）和Se（E）具体形式的求导和表达很是复杂，必须详细地分析入射离子对原子核和电子的相互作用包括碰撞。原子核和电子对入射离子的阻止作用究竟哪一种为主涉及入射离子的能量，速度，质量和靶材料的原子质量和原子数目。通常在低能量入射和入射离子质量较大时原子核阻止为主要因素；而高能量入射和靶原子核质量较小时，电子阻止为主要机制。在这里只给出Sn（E）和Se（E）简单推导和表达。

（1）原子核阻止能力Sn（E）理论计算。在计算Sn（E）时需求出入射离子通过微分射程dx时与靶原子核相碰撞而损失的能量。图7-16给出了一个入射离子（质量为m1，初始能量为E1，速度为v1，电荷为Z1e）与靶原子核（质量为m2，初始速度v2=0，电荷为Z2e）碰撞后的情况。

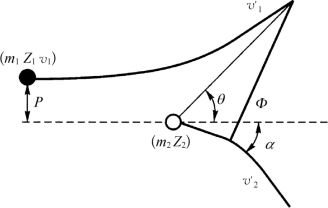
图7-16　入射离子和靶原子核碰撞

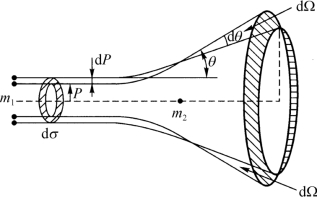
图7-17　微分截面

如果入射离子经过一个靶原子核而不被折射，其前进方向将经过离原子核为P的距离。这个距离被称为碰撞参数或碰撞概率。如果碰撞，其结果是入射离子被偏折θ角，同时伴随能量损失和转移，损失的能量EL转移给原子核，使其偏折α角。Φ为质心坐标系（CM系）中的折射角。被转移的能量EL和入射离子的初始能量E1和P有关，可认为是它们的函数，则EL可被表述为

因而入射离子通过一半无限非晶靶材（靶密度为N）内dx距离和（Ndx）2πPdP个原子核碰撞在单位路径上的能量损失可由式（7-15）求得

式中，dσ为微分散射截面（见图7-17），dσ=2πPdP，这时原子核阻止能力Sn（E）可得到

式中，（ELn）max表示入射离子和原子核对心碰撞（P=0）时最大的能量转移，其可由经典力学求得

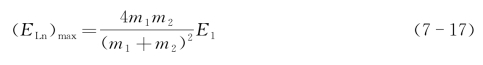
在LSS理论中，利用J.Lindhard选用的电荷屏蔽势公式

经过一定的运算可以求得微分截面dσ，见公式（7-19）

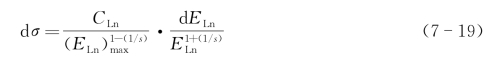
式中CLn是与核阻止能力有关的常数。s=1是简单的库仑屏蔽势；s=2是托马斯-费米势。当s在2与3之间时，理论与实验符合得好些。

有了dσ具体形式，则可以求得Sn（E）。在粗略而有用的一级近似后，可得到与入射离子能量无关的核阻止能力表达式为

式中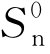，（E）的单位为eV·cm2。

同样可求得实验室坐标系下入射离子的散射角θ为

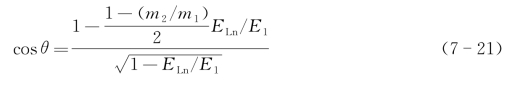
表7-2给出了一个50 keV能量的Si离子和Si靶原子碰撞时的散射角和能量损失的相关数据。

表7-2　50 keV Si离子和靶原子碰撞时的散射角和能量损失

注：表中a：屏蔽半径，等于0.1Å。

（2）电子阻止能力Se（E）理论计算。Se（E）计算比Sn（E）复杂得多，这里仅简单地介绍计算Se（E）的两种物理模型及表达。

第一种是LSS模型。LSS理论认为固体中的电子可看作自由电子气，入射离子在靶中受电子的阻力和子弹在大气中受气体分子的阻力类似，在速度不太大时其阻力和入射离子速度成v1正比，也就是与入射离子能量E1的平方根成反比，即

K数值依赖于入射离子和靶材。对于非晶材料，K几乎与入射离子的性质无关。通常K值为（0.1～0.2）×10-15[（eV）1/2cm2]，只有当Z1≪Z2时，K才大于1×10-15[（eV）1/2cm2]。Lindhard等根据Thomas-Fermi模型求得

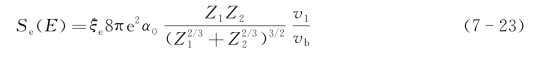
式中，，α0为玻尔半径，为玻尔速度。必须注意的是公式只有当v1≪vb时才正确。若采用实用单位，则可得

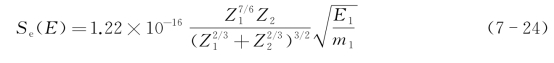
式中，Se（E）的单位为eV·cm2。

第二种是弗索娃（Firsov）模型。Firsov考虑到Se（E）随Z1和Z2周期性振荡的效应，提出一个稍微不同的模型应用于非晶靶的计算。其计算程序与原子核阻止能力计算类似，先计算入射离子在靶内碰撞由电子作用而损失的能量ELe，然后假定靶粒子是无序分布，因而得出

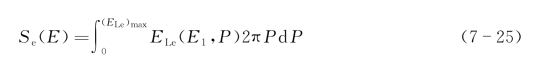
Firsov证明，原子由负经过靶原子再运动到正时，由于核外电子的作用，总的能量损失可由公式（7-21）近似表达

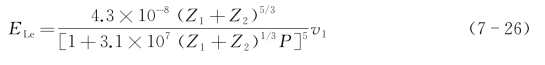
式中v1和P的定义和原子核阻止能力计算中的定义相同。上述公式只在入射离子速度v1小于这两个原子的外围电子的轨道速度时才适用。

3.根据Sn（E）和Se（E）估算射程及入射离子在非晶靶中的浓度分布

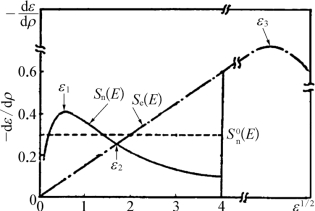
（1）射程估算。根据上述讨论可画出Sn（E）和Se（E）值随入射离子能量变化的理论曲线（见图7-18）。由图7-18可知：

(www.xing528.com)

图7-18　Sn（E）和Se（E）的理论曲线

Sn（E）和Se（E）的能量变化曲线都有一个最大值。Sn（E）的最大值发生在低能区（ε1）而Se（E）能量最大值发生在高能区（ε3）。

两条曲线的交界处存在一个临界能量（ε2）。在低能区核阻止占优势，电子阻止可忽略；在高能区，电子阻止占主要地位，核阻止可不计；在中能区（ε2附近的范围相当宽的一个区域），核阻止和电子阻止同等重要，必须同时加以考虑。

一是低能区射程估算。根据式7-8可计算入射离子的平均总射程R，由于在低能区电子阻止可以不考虑，用Sn（E）的一级近似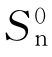（E）估算射程则可得射程R为

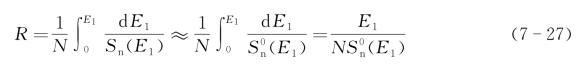
二是高能区射程估算。在高能区，原子核阻止可不考虑，则射程R为

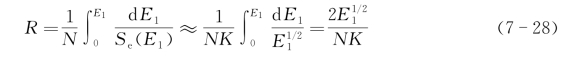
射程的标准偏差是表征射程分布的一个重要参数，定义为射程的平均平方涨落，即

通常可用ΔR2表示，于是可得

平均投影射程的标准偏差也是一个重要的参量见图7-19，它决定离子在靶中浓度分布的形式，RP的标准偏差与R的标准偏差相似，可写成

（2）浓度分布。作为一级近似，非晶靶中入射离子的浓度分布可用高斯函数来表示，入射离子的浓度可表达为

式中，x为入射离子沿入射方向在靶内离开靶表面的距离，C（x）为该处的离子浓度。由式（7-30）可知，在x=RP处浓度最大，为峰浓度。一般情况下入射离子的计量Q是受控的，即已知的，通过确定Q和Cmax的关系可求得Cmax的值。

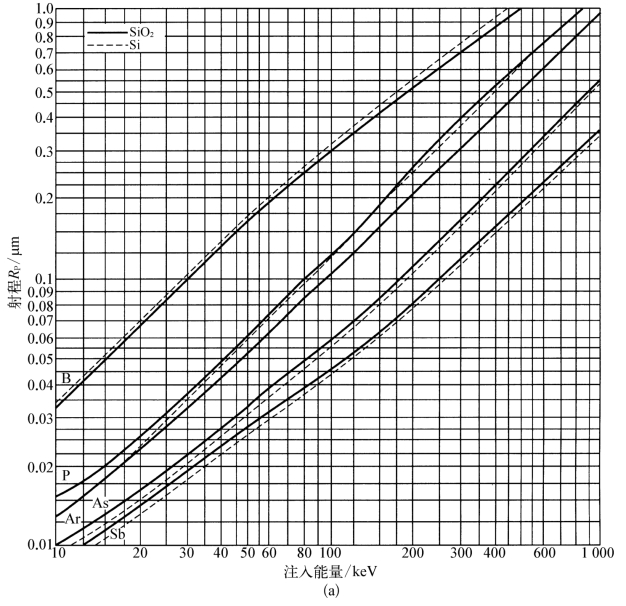
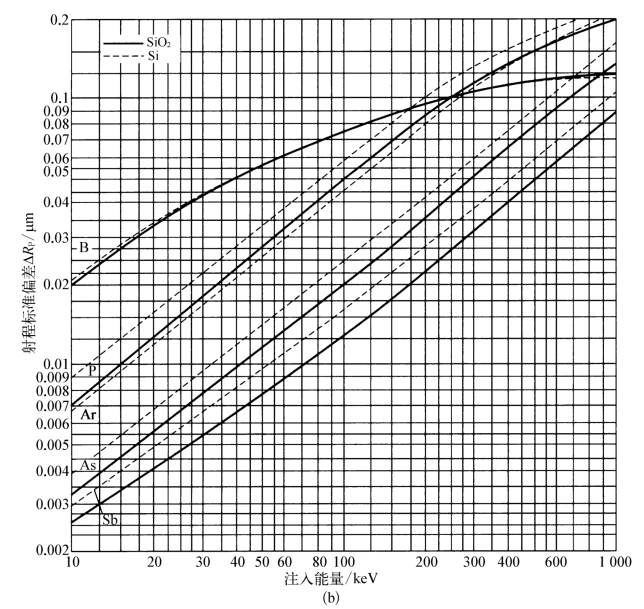
图7-19　Si和SiO2离子注入射程和射程标准偏差

（a）射程与注入能量关系（b）射程标准偏差与注入能量关系

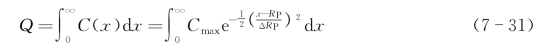
令X=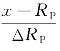通过积分变换可得

利用（7-30）关系式就可得到入射离子在靶中的浓度分布

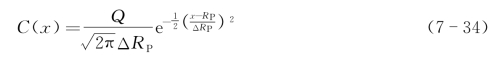
图7-20给出了入射离子浓度分布曲线。从图中可看出在x=RP处有最高浓度Cmax；在RP两边入射离子浓度对称下降。

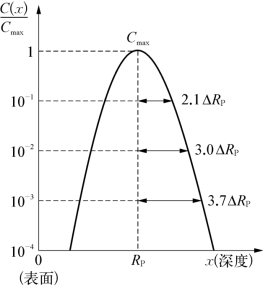
图7-20　入射离子浓度分布曲线

4.单晶靶中的射程分布和沟道效应

（1）沟道效应。前面所讨论的主要是入射离子在非晶靶中的射程分布，非晶靶的原子排列是杂乱无章的，入射离子所受到的碰撞过程是随机的，受到的阻止是各向同性的，因此入射离子在不同方向射入靶中将得到相同的射程。但在单晶靶中，原子的排列是有规律和周期性的，因此靶对入射离子的阻止作用是各向异性的，取决于晶体的取向，因而入射离子在不同方向上的入射将得到不同的射程。当入射离子沿某些低指数轴向入射时，入射离子有可能沿晶轴方向穿透的比较深，这种现象称之为离子注入的沟道效应。

图7-21给出了单晶Si沿〈110〉晶向的原子排列模型和沿〈110〉轴偏离8°观察时的原子排列模型。当沿〈110〉方向观察时，可看到一些由原子列包围成的直通道（沟道）。当入射离子沿此方向进入沟道时，其轨道将不再是无规则的，而是在沟道中运动，这时靶阻止作用小导致入射离子的射程变大，形成沟道效应。当偏离〈110〉方向观察时，原子的排列相当紧密而紊乱，入射离子沿此方向注入时将受到较大的阻止作用，与非晶靶材情况类似，不会产生沟道效应。

图7-21　硅晶格的不同晶向原子排列模型

（a）〈110〉方向（b）偏转8°

入射离子进入沟道并不意味着一定发生沟道效应，只有当入射离子的入射角小于某一角度φc时才会发生，这个角称为临界角。图7-22给出了入射离子注入沟道时的碰撞情况。在图7-21（a）中，当离子A以大于临界角φc入射时，将与晶格原子严重碰撞而不产生沟道效应；当离子B以稍小于临界角的角度入射，它将在沟道内受到较大的核碰撞而损失较多的能量，因而在沟道中振荡，但比A入射更深；当离子C以远小于临界角的方向入射，它在沟道中很少受到原子核的碰撞，可入射的很深。图7-23显示了入射离子其入射位离晶轴位置不同而产生的不同碰撞情况。当A沿着靠近晶轴位置入射时，很容易与晶格原子碰撞而产生大角度散射，不能进入沟道；离子B在离晶轴稍远位置入射时，受到较大的核碰撞而在两个晶面间振荡；离子C在远离晶轴的位置入射，基本不受到原子核的碰撞，可入射更深。

图7-22　入射离子以不同的入射角射入沟道

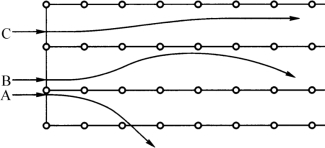
图7-23　入射离子距晶轴不同位置射入

临界角的大小可用J.Lindhard的理论来计算^[2]。当入射能量较高时，临界角为

当入射离子能量较低时，临界角为

式中d为沟道壁靶原子列中相邻两原子间的间距，c为调整参数，a为屏蔽参数，a=0.047-1/2（nm）。表7-3给出了单晶Si中的沟道效应临界角。

表7-3　单晶的沟道临界角（°）

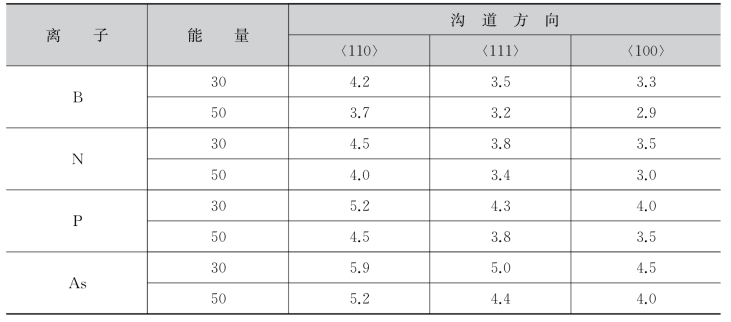
在实际生产过程中为了使掺杂元素在器件中分布尽量能够均匀，在实际生产上会采取一定的预防措施来防止沟道效应。通常所用的方法包括：①控制入射离子入射方向与硅晶片晶面取向之间的角度；②在硅表面镀上一层非晶硅；③将硅晶片表面预先用Ar离子处理使之形成非晶层或用光掩膜胶涂覆。

（2）单晶靶中的射程分布。一束入射方向平行于晶轴的入射离子，不一定都会进入沟道。一部分因大于入射临界角或靠近晶轴位置而被靶原子散射掉，这部分称之为随机束。它们在靶中的分布和在非晶靶中分布类似，在靶表面形成高斯分布。另一部分离子进入沟道，并分为两种不同的情况。其中，一部分离子几乎很少受到靶原子核的碰撞，而以很长的波长在沟道中运动。它们主要受到靶内电子的碰撞或散射而损失能量，最终停留在靶内某一位置。另一部分以稍小于临界角或比较靠近晶轴位置入射，因而在沟道中振动频率较高，波长较短，容易受靶原子的碰撞，甚至中途退出沟道。

入射离子在单晶靶材中的射程分布估算可分为两种不同情况。

第一种情况是低能入射。在低能入射中核阻止占优，电子阻止可忽略，这时最大射程可由式（7-27）表示，通过计算可得沟道离子的最大射程为

式中G0为几何因子。晶格的热振动在决定低能离子入射的射程分布中起主要作用。

第二种情况是较高能量入射。在较高能量入射情况下，只要离子保持在沟道内运动，其轨道的绝大部分离原子列较远，因而核阻止作用较小，电子阻止占优，则最大射程

将Se（E1）=代入，可得

公式（7-34）只能表示，并不能直接用于计算Rmax，因为离子进入沟道时，在单位长度射程上所受到的碰撞次数并不直接由靶原子体密度N决定，而是由沟道轴周围原子排列的情况所决定；同时沟道中电子阻止本领的K值与非晶靶不同。

影响单晶靶中注入离子射程分布的因素很多，包括注入离子能量、晶体取向、温度、离子剂量和注入离子的种类等。