测量薄膜厚度和折射率的优越性与应用

集成电路工程中最常用的薄膜厚度测量首推椭圆偏振测量仪（Ellipsometry），这是一种简单易行的、非破坏性的薄膜厚度与折射率测量方法。其次，可以用SEM和TEM方法（见下一节）通过切片与观察截面形态的方式测量薄膜厚度，结合EDS可对化学成分与组分一并进行分析。

椭圆偏振仪的原理是利用一已知偏振态之偏极光，入射待测物质，量测出射光与原先入射光间的偏振态变化，来反推待测物质光学特性。椭圆偏振仪测量薄膜厚度和折射率具有独特的优点，是一种较灵敏（可探测薄膜小于0.1 nm的厚度变化）、精度较高（比一般的干涉法高一至二个数量级）并且是非破坏性测量，是一种先进的测量薄膜纳米级厚度的方法。它能同时测定膜的厚度和折射率（以及吸收系数）。因而，目前椭圆偏振仪测量已在半导体集成电路制造业得到广泛的应用。这个方法的原理几十年前就已被提出，椭圆偏振仪（以下简称椭偏仪）的实验装置也不复杂，但实验数据处理却比较困难，不仅涉及非常复杂的三角函数计算，而且求解方程的非线性和非正定性更增加了数值计算的难度，一般很难直接从测量值求得方程的解析解。直到广泛应用计算机以后，才使该方法具有了新的活力。由于椭偏参数确立的方程是超越方程，无法直接由测量数据通过计算得到薄膜参量的解析解，因此由椭偏参数求得介质薄膜参数的计算便成为椭偏仪应用中的一个重要问题。

椭偏仪测量的基本思路是，起偏器产生的线偏振光经取向一定的1/4波片后成为特殊的椭圆偏振光，把它投射到待测样品表面时，只要起偏器取适当的透光方向，被测样品表面反射出来的将是线偏振光。根据偏振光在反射前后的偏振状态变化，包括振幅和相位的变化，通过解椭偏方程便可得到薄膜折射率和厚度，图5-53为一光学均匀和各向同性的单层介质膜。它有两个平行的界面，通常上部是折射率为n1的空气（或真空），中间是一层厚度为d折射率为n2的介质薄膜，下层是折射率为n3的衬底，介质薄膜均匀地附在衬底上，当一束光射到膜面上时，在界面1和界面2上形成多次反射和折射，并且各反射光和折射光分别产生多光束干涉，其干涉结果反映了膜的光学特性，可以测出相关角度与相位，并根据相关公式计算得到薄膜厚度与折射率。

设φ1表示光的入射角，φ2和φ3分别为在界面1和2上的折射角。根据折射定律有n1sinφ1=n2sinφ2=n3sinφ3

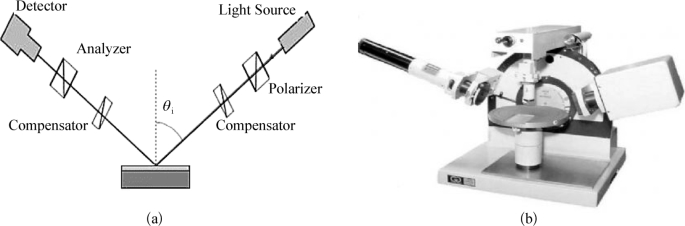
图5-53　椭偏仪的原理（a）与测量装置（b）

光波的电矢量可以分解成在入射面内振动的p分量和垂直于入射面振动的s分量。若用Eip和Eis分别代表入射光的p和s分量，用Erp及Ers分别代表各束反射光K0，K1，K2，…中电矢量的p分量之和及s分量之和，则膜对两个分量的总反射系数Rp和Rs定义为RP=Erp/Eip，Rs=Ers/Eis，经计算可得(www.xing528.com)

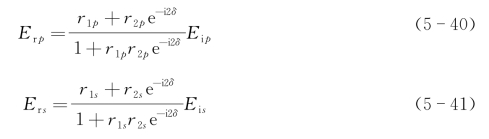
式中，r1p或r1s和r2p或r2s分别为p或s分量在界面1和界面2上一次反射的反射系数；指数上的i为虚数单位；2δ为任意相邻两束反射光之间的位相差。

根据电磁场的麦克斯韦方程和边界条件，可以证明

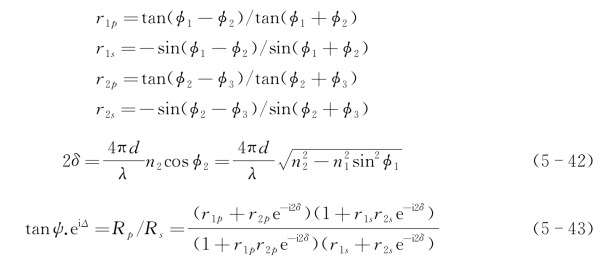
式中，λ为真空中的波长，d和n2为介质膜的厚度和折射率，2δ是由相邻两反射光束间的程差，在椭圆偏振法测量中，为了简便，通常引入另外两个物理量ψ和δ来描述反射光偏振态的变化。它们与总反射系数的关系定义为椭偏方程，其中的ψ和δ称为椭偏参数（由于具有角度量纲也称椭偏角）。

由方程（5-42）和（5-43）可以看出，参数ψ和Δ是n1，n2，n3，λ和d的函数。其中n1，n2，λ和φ1可以是已知量，如果能从实验中测出ψ和δ的值，原则上就可以算出薄膜的折射率n2和厚度d。这就是椭圆偏振法测量的基本原理。