三向应力屈服图形分区与低载荷成形范围

1.三向应力状态屈服图形的分区

对于三向应力状态，以上分析的方法大体上仍然是适用的，但是在三向应力状态下典型工序在其上的部位是难以表达的，首先需要解决在纸面上（二维空间）如何描述三向应力的问题，其次加载路径也远比平面应力状态难以描述。

由前面分析可知，任何一点的应力状态在屈服表面上都有一个点与其对应。该点可以用其至π平面的距离及π平面中的一个向量表示。对于理想刚塑性体，Mises圆柱面的半径是一常数，等于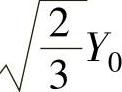（Y₀为起始屈服应力），也就是说向量的长度是不变的，所变的仅是向量的角度，于是有可能用平均应力σ_m及π平面中向量与σ₁轴投影的夹角θ来描述一点的应力状态，但这时需找到σ_m、θ与主应力σ₁、σ₂及σ₃之间的对应关系。

由于空间任一坐标（a，b，c）可以看成三个与坐标轴平行的平面σ₁＝a、σ₂＝b及σ₃＝c的交点，但在以π平面为基面的圆柱展开面σ_θ-θ平面中仅圆柱上的与π平面平行的圆周展开后的σ_m值为直线（见图6-33）。对于其他任何平面，例如σ₁＝a及σ₁＝0两平面与圆柱面所交圆环在以π平面为基面上展开而得到的σ_θ-θ平面中，就不是直线，按投影

几何应该是一个余弦或正弦曲线（两者在相位上差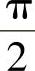）。即

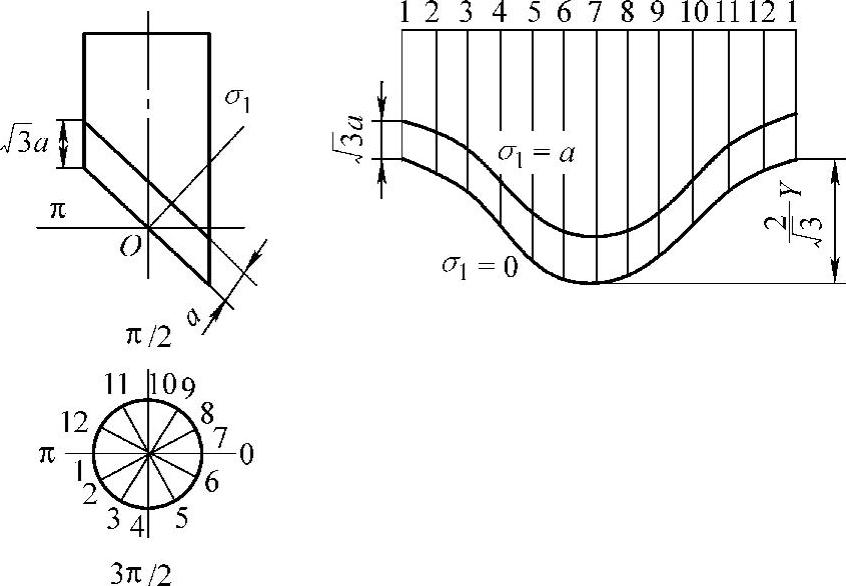
图6-33 σ₁＝0及σ₁＝a平面与Mises圆柱交线展开图

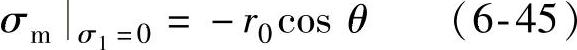
式中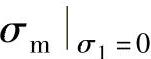，代表σ₁＝0平面与Mises圆柱面相交的轨线在σ_θ-θ平面展开后所对应的σ_m值，对于任一θ值，相应的σ_m值可以代表σ₁＝0，也就是说可以将该曲线视为变量σ₁的基线，θ从σ₁轴在π平面上的投影算起，r₀为展开曲线的波幅，对于σ₁＝a平面其展开图形完全相似，仅起点提高了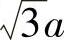，于是将有

式中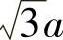，相当于σ₁的变化使所截平面沿圆柱轴线的移动量，相当于使σ_m增值，从长度上看比例放大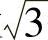倍，在一般情况下将有

σ₁＝σ_m+r₀cosθ （6-47）

请注意此时的σ₁已经是σ_θ-θ图中用σ_m高低表示的“σ₁”，从“σ₁＝0”线量起，并不是直接用主应力空间中σ₁轴度量，σ_m值用该点到π平面的距离表示，比例尺比坐标轴上距离放大3倍。同理，由于问题的对称性，可以写出σ₂及σ₃的表达式汇总如下

式中 σ_m——平均应力；

r₀——平行于坐标面的任一平面与Mises圆柱交线随圆柱展开后所得余弦曲线的波

幅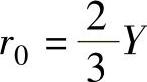，（若考虑放大3倍，则实际幅高为）。

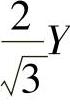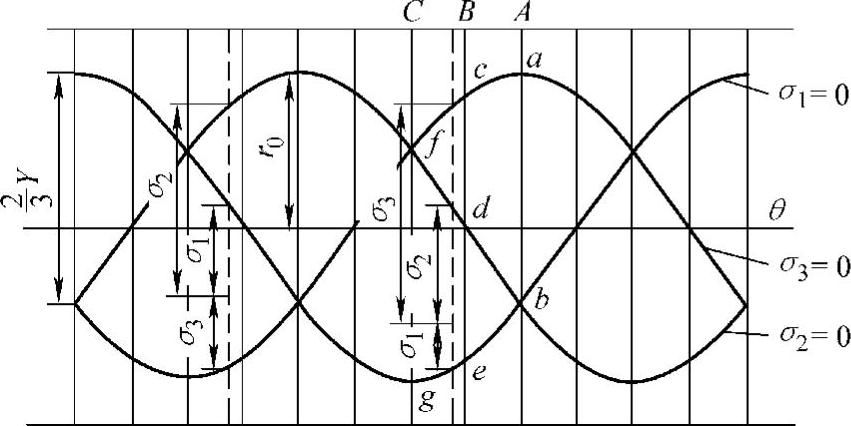
图6-34 Mises圆柱面交线的展开及主应力的表示方法

由式（6-48）可见，当σ_m及θ已知，则σ₁、σ₂及σ₃可求出，应力状态也就被确定。式（6-48）可用图6-34表示，若已知一点的σ_m及θ值可在图中找出一点。这时度量σ₁、σ₂及σ₃的大小是用图6-34中一点到σ₁＝0、σ₂＝0及σ₃＝0的距离来表示的，这三根曲线是式（6-48）左端为零时得出的。它们可作为计量的起点。由于这些曲线每隔120°就出现相似图形，而且在每120°范围内，例如0°～120°、120°～240°、240°～0°区域内的图形是对称的。所以仅研究1/6圆周就可以反映最一般的情况，现在来研究0°～60°区间的情况（见图6-35），它相当于图中π平面上σ₁＞σ₂＞σ₃区间，这时根据受拉受压情况的不同可以有以下四种应力状态，每一种应力状态在图6-35中都有一定的部位。σ₁＝0以下各点为0＞σ₁＞σ₂＞σ₃，是三向压应力状态；σ₂＝0及σ₁＝0之间（即beg线与fdb线间）各点为σ₁＞0＞σ₂＞σ₃，是两压一拉应力状态；σ₂＝0及σ₃＝0两曲线之间（即fdb与acf线之间）各点为σ₁＞σ₂＞0＞σ₃，是两拉一压应力状态；σ₃＝0（acf线）以上为σ₁＞σ₂＞σ₃＞0，是三向拉应力状态。σ₁＝0、σ₂＝0及σ₃＝0三条曲线分别代表三种平面应力状态，即分别为双向压应力状态、一拉一压应力状态和双向受拉应力状态。它们是上述四种三向应力状态的过渡态。前已述及应力状态的类型取决于中间主应力的相对大小。

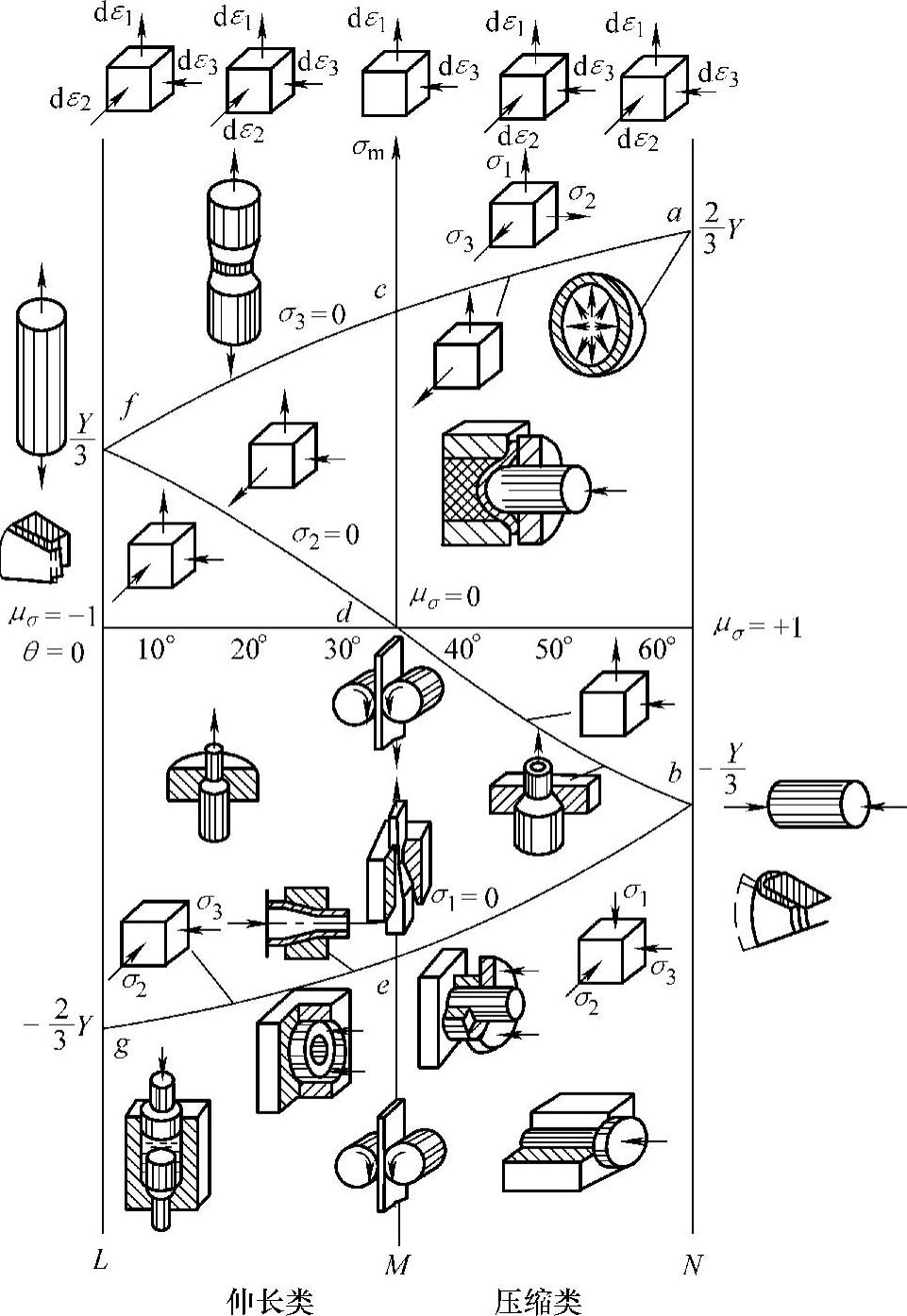
图6-35 Mises圆柱展开面上的应力应变分区

罗德参数μ_σ为

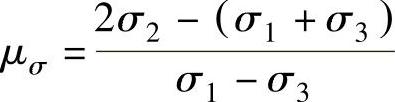
可以作为衡量应力状态的一个参数，例如简单拉伸，σ₁＝Y，σ₂＝σ₃＝0，μ_σ＝-1，θ＝60°；简单压缩，σ₁＝0，σ₂＝0，σ₃＝-Y，μ_σ＝+1，θ＝60°；平面应变时σ₂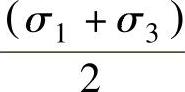＝，μ_σ＝0，θ＝30°。角ω与μ_σ之间存在以下关系，即

其中，θ与ω及μ_σ之间对应关系见表6-1。鉴于θ与μ_σ有上述定量关系，后者又是决定应变状态或者应变类型的，所以可以将θ角简称为应变状态角。

表6-1 θ角与ω角及罗德系数μ_σ的关系

在图6-35中，L线为σ₃＝σ₂，μ_σ＝-1属于“简单拉伸”类应力状态（意指产生的应变与简单拉伸相似）。M线代表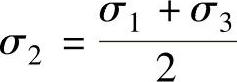，μ_σ＝0属于平面应变。N线代表σ₁＝σ₂，μ_σ＝+1属于“简单压缩”类应力状态。对于N线与M线之间的各应力状态，位于σ₂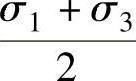＞的区间，即μ_σ＞0，应变为压缩类。位于M线与L线之间的各应力状态，位于σ₂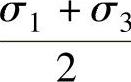＜的区间，即μ_σ＜0，应变为伸长类。因此由应力状态在圆柱或其展开面内的位置，即可判断此类应变是伸长类、压缩类或平面应变类。塑性加工中常见三向应力成形工序在Mi-ses圆柱面上的位置可由图6-35看出。

由图6-35还可以看出，当塑性加工中的工序处于该图的位置越低，则压应力就越显著，塑性越高；反之，则塑性越差。

还应指出，同一种变形状态可以与不同应力状态对应。例如简单拉伸、棒料拉拔及静液挤压应力状态各不相同，但皆产生伸长类应变状态，其原因主要是由于μ_σ或θ相近，仅相差一个平均应力σ_m，而前面已指出平均应力是不影响形状变化的。拉伸、拉拔及静液挤压应力偏量为同一类型，所以应变也为同类型。

应该指出，图6-29及图6-35两个图是首次给出平面应力及三向应力状态的各成形工序的应力、应变、屈服图形和尺寸变化趋势的统一结果。

2.三向应力低载荷成形在屈服图形上的范围

从图6-35可以看出σ_m、σ₁、σ₂及σ₃的相对高低，通常所谓载荷是指工具作用到工件上的力，仅与某一个或两个主应力发生直接关系。例如，环形件闭式镦粗作用力载荷，仅是垂直于环的端面发生直接关系。当然由于模套的限制，也会产生来自侧壁的压力，对变形流动产生影响；对于带张力轧制，载荷主要是来自轧辊施加于轧件的压力和卷取机施加于轧件上的拉力。由于必须满足屈服准则，σ_m、σ₁、σ₂及σ₃之间的差别并不是很大，以下分三种情况来进行分析。

（1）平面应变类 在图6-35中为μσ＝0，对应于M线，此时的应力摩尔圆，当0＞σ₁＞σ₂＞σ₃时，即为三向压应力，如图6-36a所示，此时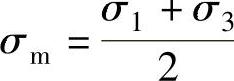＝σ₂＜0，应力摩尔圆处于原点左侧。应力摩尔圆大圆的直径σ₁-σ₃可根据Mises屈服准则求得，即当μ_σ＝0时其为

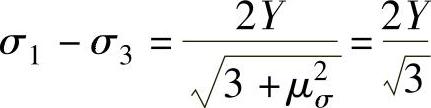
由于σ₁-σ₃为应力摩尔圆直径，此数值仅取决于材料流动应力Y与罗德系数μ_σ，当σ_m变化时应力摩尔圆的形貌不变，仅改变其在σ轴上的位置。例如，图6-36b、c分别表示当σ₁＞0＞σ₂＞σ₃及σ₁＞σ₂＞0＞σ₃时的应力摩尔圆。(www.xing528.com)

由图6-36a、b、c可见，σ_m与σ₁及σ₃的差值均为应力摩尔圆大圆的半径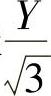，即

及

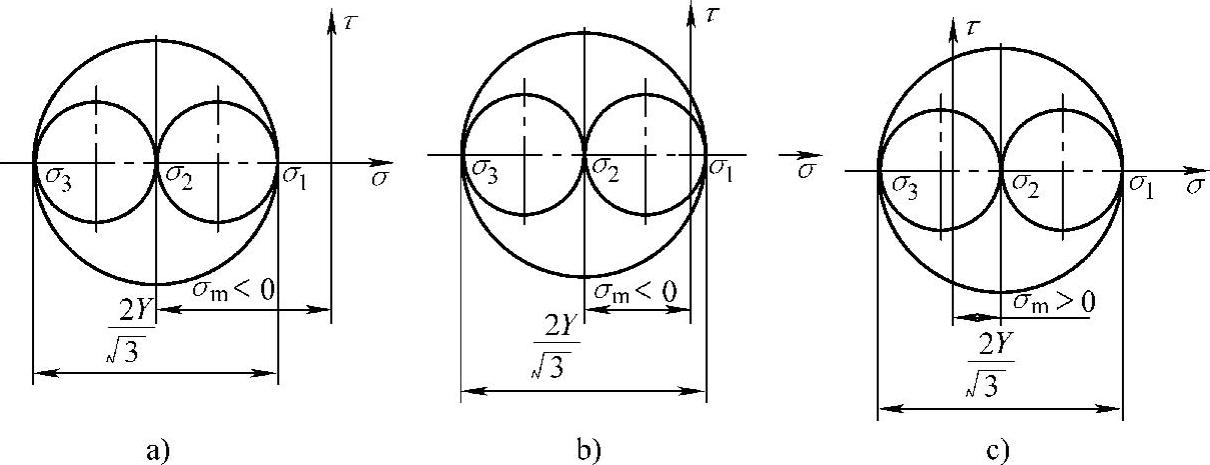
图6-36 当μ_σ＝0时的应力摩尔圆

a）0＞σ₁＞σ₂＞σ₃ b）σ₁＞0＞σ₂＞σ₃ c）σ₁＞σ₂＞0＞σ₃

（2）拉伸类应变 对于简单拉伸类变形状态如图6-35中的L线，此时的μ_σ＝-1，dε₁＞0，dε₂＝dε₃＜0，应力摩尔圆大圆直径（μ_σ＝-1时）为

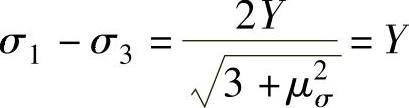
当应力状态不同时，应力摩尔圆有以下几种形式，当σ₁＞0＝σ₂＝σ₃，0＞σ₁＞σ₂＝σ₃，相应的摩尔圆如图6-37a、b所示。

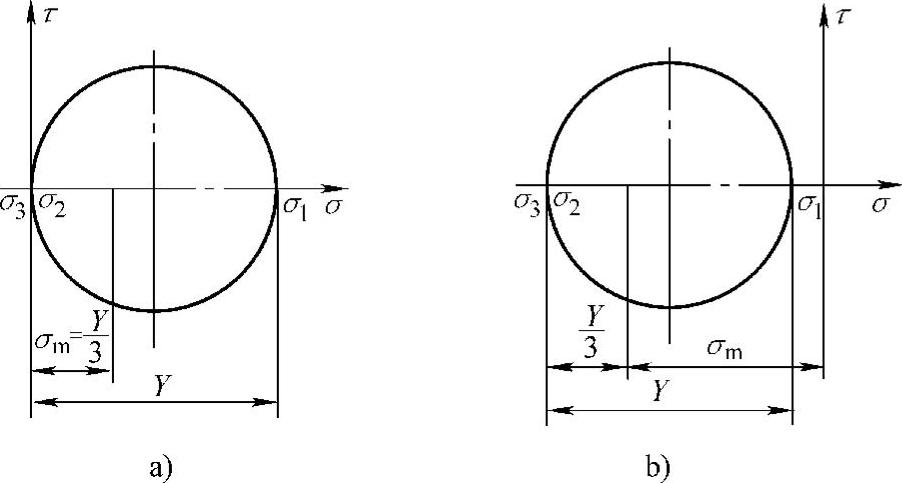
图6-37 当μ_σ＝-1时的应力摩尔圆

a）σ₁＞0＝σ₂＝σ₃ b）0＞σ₁＞σ₂＝σ₃

这时σ_m为

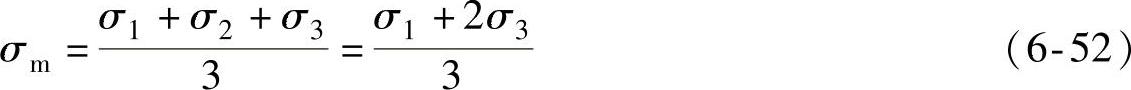
将屈服方程σ₁-σ₃＝Y代入式（6-52）可得

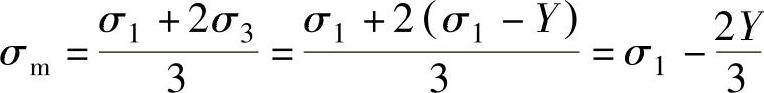
也就是

同时又可根据σ₁-σ₃＝Y和式（6-53）求出，即

（3）压缩类应变 对于简单压缩类变形，此时如图6-35中的N线。此时μ_σ＝+1，dε₁＝dε₂＞0，dε₃＜0，应力摩尔圆大圆半径（μ_σ＝+1时）为

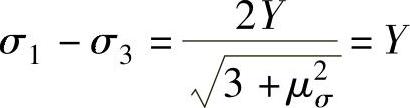
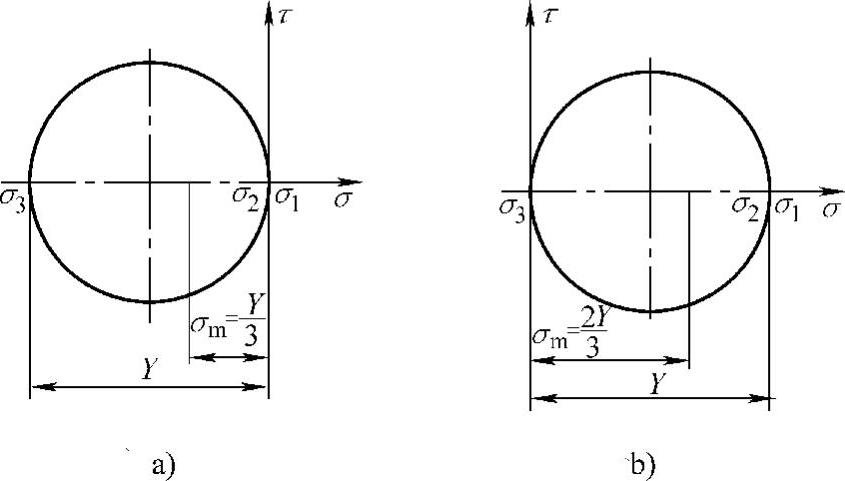
图6-38 当μ_σ＝+1时的应力摩尔圆

a）σ₁＝σ₂＝0＞σ₃ b）σ₁＝σ₂＞σ₃＝0

当应力状态不同时，应力摩尔圆有以下几种形式，当σ₁＝σ₂＝0＞σ₃及σ₁＝σ₂＞σ₃＝0，此时的应力摩尔圆如图6-38a、b所示。由图可见

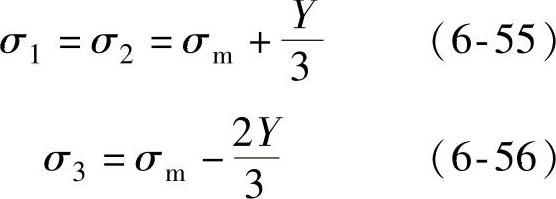
由图6-36～图6-38及式（6-50）～式（6-56）可见：

1）应力摩尔圆的形貌取决于中间主应力σ₂偏离大圆圆心的程度，可利用μ_σ来表征，对于平面应变μ_σ＝0，对于简单拉伸类变形μ_σ＝-1，对于简单压缩类变形μ_σ＝+1。

2）应力摩尔圆在横轴σ上的位置主要取决于σ_m值，对于特定的μ_σ值，σ₁-σ_m及σ₃-σ_m值也随之而定。

3）σ_m值与σ₁及σ₃的最大差值为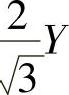（对于简单拉伸类应变和简单压缩类应变）或Y（对于平面应变类）。

4）由此可见，图6-35可以作为衡量载荷高低的重要依据，因为对于任何一个σ_max或σ_min与σ_m的差值均小于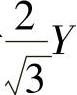，所以尽管载荷的作用方式不同，当σ_m越大，即平均压应力或平均拉应力越大时，都会导致成形载荷的上升。

根据上述分析，低载荷成形区为Y＞σ_m＞2Y，如图6-39所示。图6-39中下部无边界，而上部取Y为边界的原因是在现实成形工序中拉应力过大会导致破裂，而在三向压应力时，尽管σ_m的绝对值很高也不至破裂。

图6-39根据σ_m值的不同，大致上分为：I区，即最低载荷成形区；II区与III区，即稍低载荷成形区，分别对应于拉压不同应力状态；IV区，即高载荷成形区；V区，即最高载荷成形区。

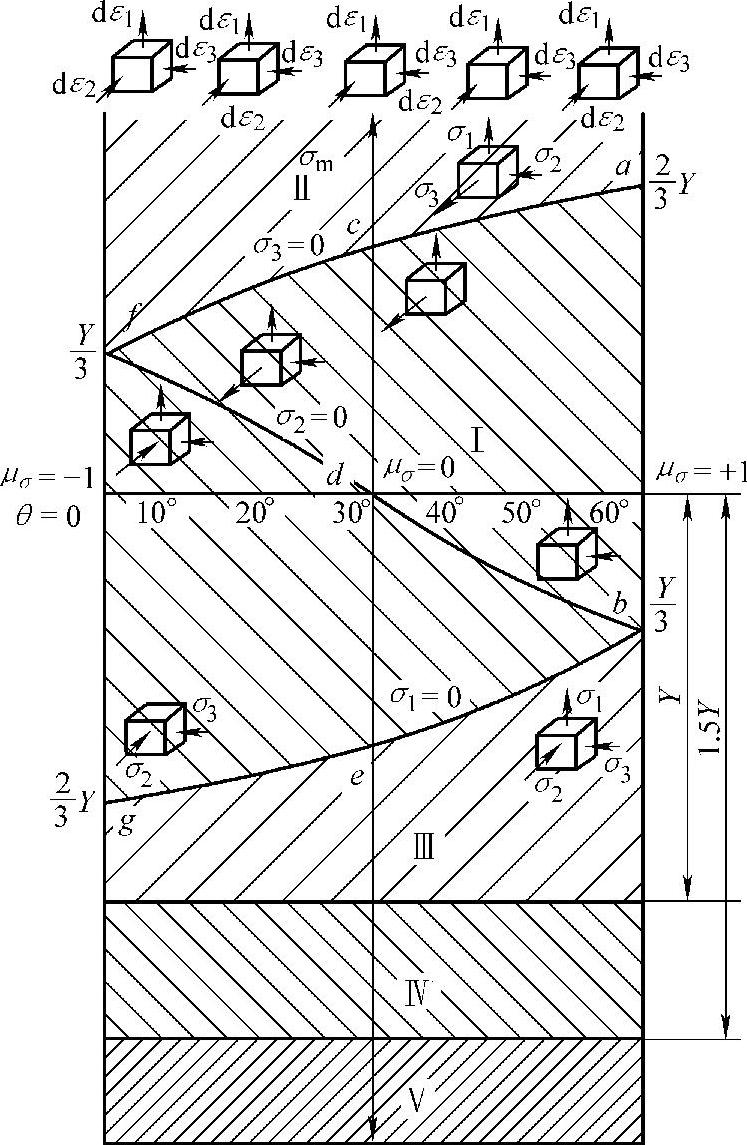
图6-39 不同载荷成形区域