平面应力屈服图形分区与省力成形范围探究

1.平面应力屈服图形的分区

前面曾分别谈到屈服准则及应力应变关系理论，以下将讨论两者间的关系能否结合具体塑性加工工序从图形上表示出来。首先，根据特定工序的受力分析找出它在屈服表面上所处的部位，进而找出变形区中不同点在屈服面上所对应的加载轨迹；其次根据应力应变顺序对应规律将屈服轨迹上的应力状态按产生的应变（增量）类型进行分区，找出工件各部分尺寸变化的趋势。

现在先分析轴对称平面应力状态下屈服轨迹上的应力分区及典型平面应力工序的加载轨迹，以薄板成形为例进行研究。设板厚方向应力为零，即σ_t＝0。对于由径向应力σρ、环向应力σ_θ为坐标轴所描述的应力椭圆方程为

σ²_θ-σ_ρσ_θ+σ_ρ²＝Y² （6-39）

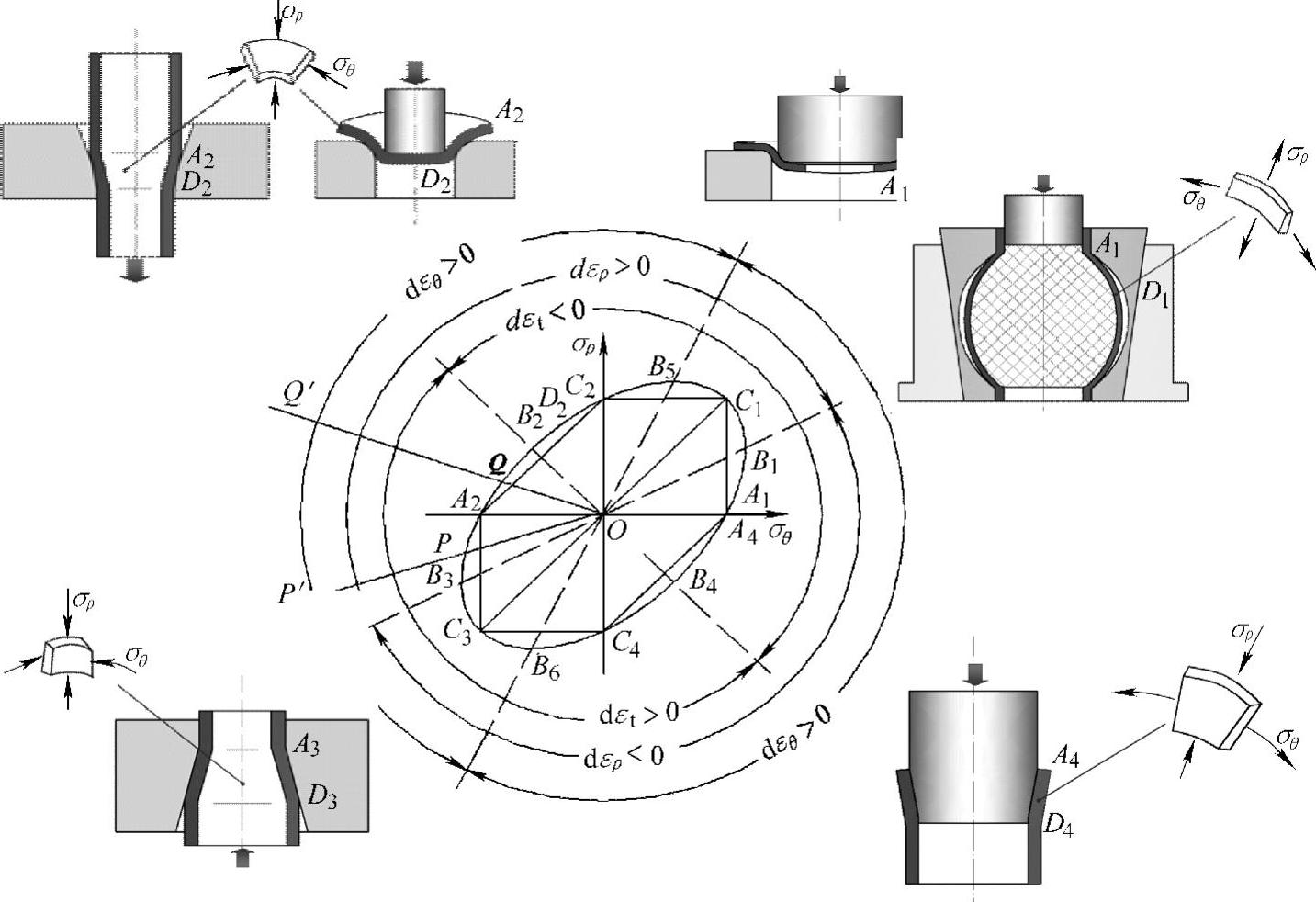
图6-29 平面应力状态屈服轨迹应力分区

其图形如图6-29所示。该椭圆第I象限σ_ρ＞0，σ_θ＞0，与胀形工序及翻孔工序相对应；在第II象限σ_ρ＞0，σ_θ＜0，与拉拔及拉深工序相对应；第Ⅲ象限σ_ρ＜0，σ_θ＜0，相当于缩口工序；第Ⅳ象限σ_θ＞0，σ_ρ＜0，相当于扩口工序。根据应力应变顺序对应规律对屈服图形上的应变进行分区，进而可以判断工件在变形区中各处的变形倾向，即尺寸变化的趋势，以下作具体说明。例如对于拉拔工序凹模入口处A₂为σ_θ＝-Y，σ_ρ＝0，随着变形的发展由椭圆上A₂出发沿椭圆向C₂前进，凹模出口处D₂所对应点在椭圆上的位置取决于σ_ρ值的大小。若变形量小、润滑好，则σ_ρ较小，D₂可能落在A₂B₂区间；若变形量大，润滑效果差，则D₂落在B₂C₂区间。图中B₂点的应力状态按顺序为：σ₁＝σ_ρ，σ₂＝σ_t＝0，σ₃＝σ_θ＝-σ_ρ，此时中间主应力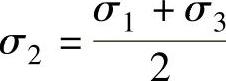，由此可见沿该方向的应变增量为零，即dε_t＝0，也就是说厚度不变，对于A₂B₂区间，恒满足σ₂＝σ_t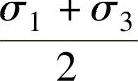＞。由应力应变顺序对应规律可以判断在A₂B₂区，dε_ρ＞0，即长度增加；dε_t＞0，即厚度增加；dε_θ＜0，即圆周缩小。如果轴向拉压力σ_ρ不大，例如薄壁管拉拔，变形以后壁厚总会增加。

对于B₂C₂区，σ_ρ仍为最大主应力σ₁，σ_θ仍为最小主应力σ₃，沿厚度方向主应力σ₂＝σ_t仍为零，但此时σ₂＝σ_t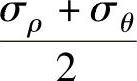＜，由应力应变顺序对应规律可以判断在B₂C₂区，dε_ρ＞0，dε_θ＜0，厚度方向从B₂点开始减薄，dε_t＜0。同样可以说明在椭圆上还存在另外五个平面应变点B₁、B₃、B₄、B₅、B₆，其中B₄与B₂相对，都是|σ_ρ|＝|σ_θ|，但符号相反，都对应dε_t＝0，对于椭圆上B₂B₃B₆B₄区段总存在以下关系，即

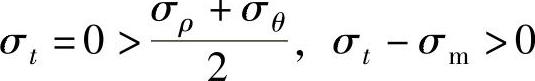
由增量理论知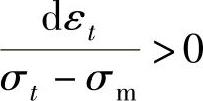：，所以dε_t＞0。可见在B₂B₃B₆B₄区间变形，则ε_t＞0。对于B₂B₅B₁B₄区段与前述相反，即

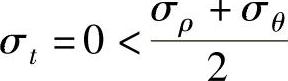
于是有

dε_t＜0

如果在该区段变形，则ε_t＜0。以上两种情况构成图6-29所示屈服图形的内圆。

对于缩口工序，属于双向压应力状态，B₃点的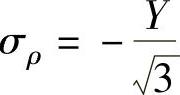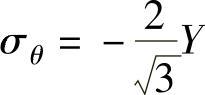，，而σ_t＝0。可见此时存在下列关系，即

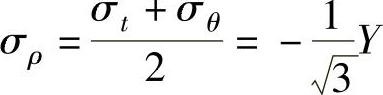
与前类似，由Lévy-Mises方程可以断定dε_ρ＝0。

对于B₁点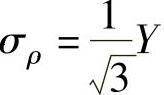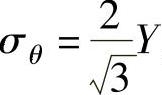，，，σ_t＝0，同样存在以下关系，即

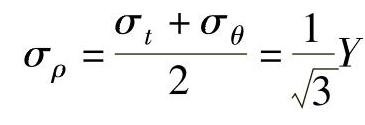
同理将有dε_ρ＝0。

在B₃B₂B₅B₁段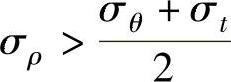，，于是相应地有，dερ＞0。在该区段变形，ερ＞0。在B₃B₆B₄B₁段正相反，在该区变形将有ε_ρ＜0。

也可用以上相同的方法求得dε_θ﹥0，dε_θ＝0，dε_θ＜0的分区。它对应于图6-29所示屈服图形外的外圆。汇总起来就得到图6-29所示的屈服轨迹外的应变增量变化图。该图是首次将屈服图形、应力分区、应变增量变化趋势与各平面应力成形工序给出统一的图解。利用该图还可以确定变形时工件尺寸变化的趋势。其大体步骤如下：

1）通过实测载荷（例如拉拔力、缩口力）算出工件中对应点的应力σ_ρ值。

2）针对具体材料及变形量选定Y值。

3）在椭圆对应于所分析的区间根据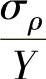值求出一点P。

4）作射线OPP′与椭圆外的表示应变增量的三个圆相交。

5）根据变形区所处的范围判断各方向尺寸变化的趋势。

2.平面应力低载荷成形在屈服图形上的范围

从平面应力屈服图形（见图6-29）上看，位于第Ⅱ象限及第Ⅳ象限均为异号应力，即σ_ρ与σ_θ的符号相反，根据屈服准则有

|σ_ρ|+|σ_θ|＝1.1Y （6-40）(www.xing528.com)

因而其中的任一应力σ_ρ或σ_θ的绝对值均小于材料的流动应力Y的1.1倍。

在屈服图形上的第Ⅰ象限及第Ⅲ象限均为同号应力，必须在σ_ρ＝1.1Y或σ_θ＝1.1Y时，方能产生塑性变形。

（1）管材拉拔 对于具体的金属成形工序而言，一般有一个加载轨迹，例如对于拉拔，入口端的σ_ρ＝0，由入口向出口σ_ρ的数值不断增加，对于薄壁管拉拔当变形量不大（即D/d不大）时，σ_ρ也不大，设其数值为σ_ρ＝q（见图6-30），这时的加载轨迹就是从模具的入口到出口，相当于从屈服图形上的A₂点到Q点，原因是A₂点发生塑性变形必须满足屈服准则，对于拉拔σ_θ＜0，σ_ρ＞0，加载的必由之路就是沿屈服图形从A₂点出发走向B₂点，但终点取决于σ_ρ的数值。同理，对于厚壁管拉拔，由于变形力较大σ_ρ也增加，设σ_ρ＝d，它相当于拉拔出口处的应力在屈服椭圆上对应的点为D点，此时的加载轨迹在图6-30上是由A₂点沿椭圆上行至D点。

对于薄壁管拉拔，由于σ_ρ值相对较小，则Q点处于厚度分界B₂点之下，由原点作射线OQQ′交内圆于Q′点，此时工件由入口至出口，皆处于dε_t＞0的区间，累积起来，经过拉拔壁厚会略有增加。对于薄壁拉拔降低载荷，实际上就是降低σ_ρ，使用减摩效果好的液体润滑将会降低σ_ρ值。应当顺便提到的是，控制σ_ρ也可调节所拉拔管材的厚度，例如，对于同样的总变形量D/d，若采用多道次拉拔，则不仅载荷可以降低，而且厚度增加量可比单次大变形量拉拔时要大。对于厚壁管拉拔，如前所述，σ_ρ值较大，同样的办法，自原点O作射线经过D点外延与厚度变化的圆相交于D′点，由图可见，该D′点处于dε_t＜0，即减薄区，说明壁厚一定减薄，同样，为了减少拉拔力可以通过改进润滑和采用多道次变形来实现。生产实践表明，对于铝合金管材的拉拔，当径厚比D/t＞5时（相当于薄壁管），壁厚增加，当D/t＜5时（相当于厚壁管），壁厚减少。

（2）板材拉深 以上分析的管材拉拔属于稳态变形过程，忽略了端头的变形分析，对于非稳态变形过程，例如第Ⅱ象限的板材拉深工序，图6-31中的右上角表示拉深开始时的状态，拉深过程中坯料逐渐流入凹模形成如图6-31中右下角所示的筒形件。坯料的外缘为自由状态，径向应力σ_ρ＝0，坯料中的质点自边缘向模口σ_ρ的数值是增加的，但必须满足屈服准则，即σ_ρ沿屈服椭圆A₂M线加载，当σ_ρ到达M点时，质点处于变薄区（dε_t＜0），随着拉深过程的进行，工件外径逐渐减小，若不计加工硬化，则σ_ρ也减小。对应凹模口M处坯料中的径向应力σ_ρ值下降，这意味着M处的σ_ρ沿椭圆下移，于是变形区全部进入增厚区（dε_t﹥0）。因此法兰外缘增厚，但模口M处在拉深阶段前期处于减薄区。该处的金属变薄后通过凹模变成弹性的传力区，但仍保留了减薄状态。所以板料拉深件沿筒壁厚度是不均匀的，筒口厚、筒底圆角处最薄，且该处最易开裂。

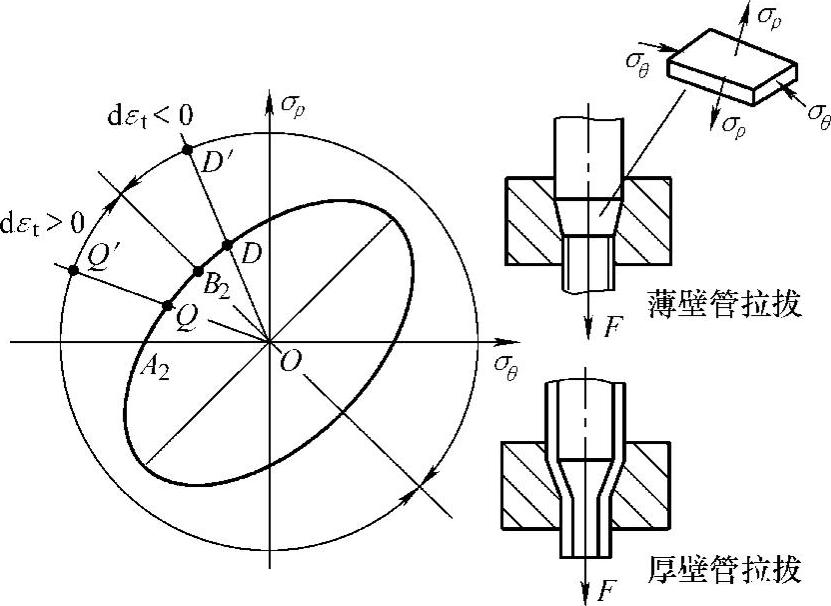
图6-30 管材拉拔应力变化轨迹

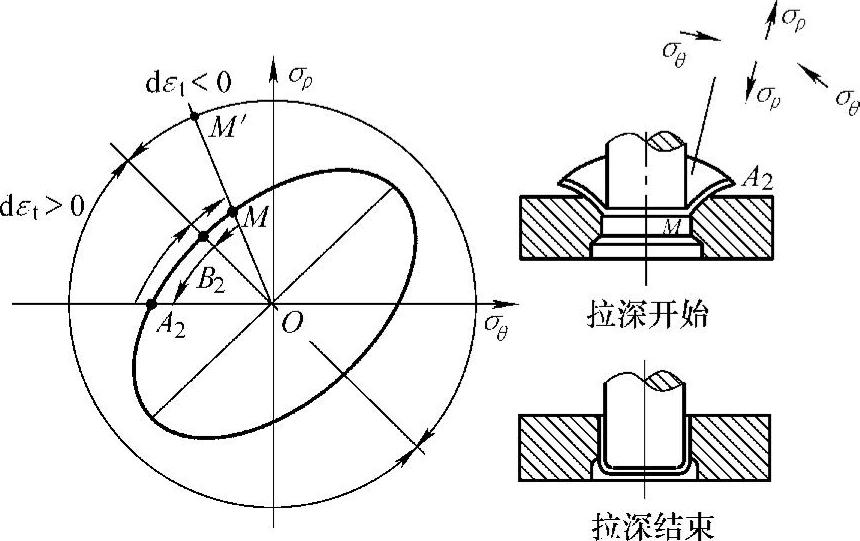
图6-31 板材拉深应力变化轨迹

减小拉深载荷的措施有很多，增加道次和将法兰部分加热（即差温拉深）都是有效的措施，实质就是使σ_ρ下降。

（3）内高压成形 内高压成形时，管件受轴向压应力，在管内受高压流体作用沿环向产生拉应力，应力状态也是异号，相当于Mises椭圆的第Ⅳ象限，如图6-32所示。

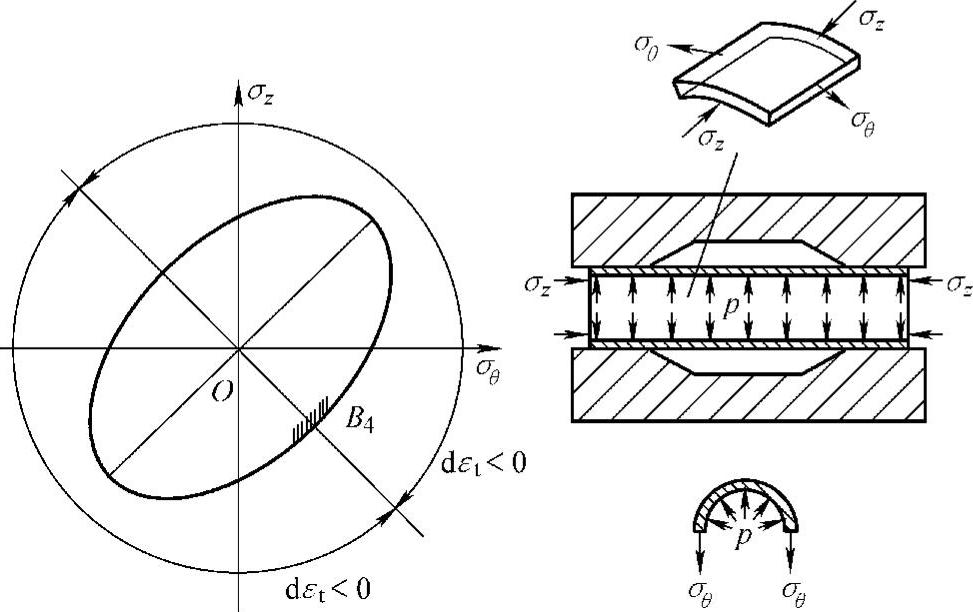
图6-32 管材内高压成形应力变化最佳范围

管材所受环向应力σ_θ计算公式为

式中 d——管材内径（mm）；

t——管材壁厚（mm）。

轴向应力σ_z为

式中 F——轴向载荷（N）；

S——管材横截面积（mm²）。

从理论上说只要满足屈服方程为

|σ_z|+|σ_θ|＝1.1Y

就可以产生塑性变形，也就是说|σ_θ|增加，|σ_z|可以小一些，或|σ_z|增加，|σ_θ|也可以小一些，但是从变形均匀性角度，在尽量控制壁厚减薄，这就要求σ_θ与σ_z的组合尽量靠近厚度不变的B₄点，即

式中 Y——材料的流动应力。

如果轴向压应力σ_z较小，则必需较大的σ_θ才能产生塑性变形，这可能导致环向开裂，与此同时，所需内压力也要较高。可用式（6-41）和式（6-43）计算出内压力，即

由式（6-44）可见，对于材料流动应力Y较高，且t/d较大的管材液压成形时，目前的高压系统（压力一般小于400MPa），也难以满足成形的要求，增大轴向应力σ_z，又会引起管材的轴向起皱，因此要综合考虑内压和轴向力的关系，才能获得理想的成形效果。图6-32中B₄点附近的阴影区域表示内高压胀形阶段的最佳应力变化范围。