因为板料要产生大位移、大转动、大变形，对于形状复杂的冲压件，如不采用高精度的单元就难以获得合理的CAE分析结果；还有一些冲压件，在成形之后还要进行裁剪和脱模回弹分析，此时就需要选择更高精度的单元公式进行模拟。因此，对于不同的计算问题，应选用与之相适应的单元公式。
在冲压成形过程中，坯料是典型的大变形构件，因此，坯料必须采用精细的网格模型，而且单元形状要尽量保证采用四边形单元（见图5-10）。
在板料成形CAE分析中，模具作为刚体，其网格一方面作为模具型面的近似描述，另一方面作为接触界面与坯料一起构成接触模型，但不参与应力与应变计算，也不影响系统的临界时间积分步长，主要考虑对模具型面的准确描述，可使用三角形单元和四边形单元（见图5-11）。
图5-10 板料网格
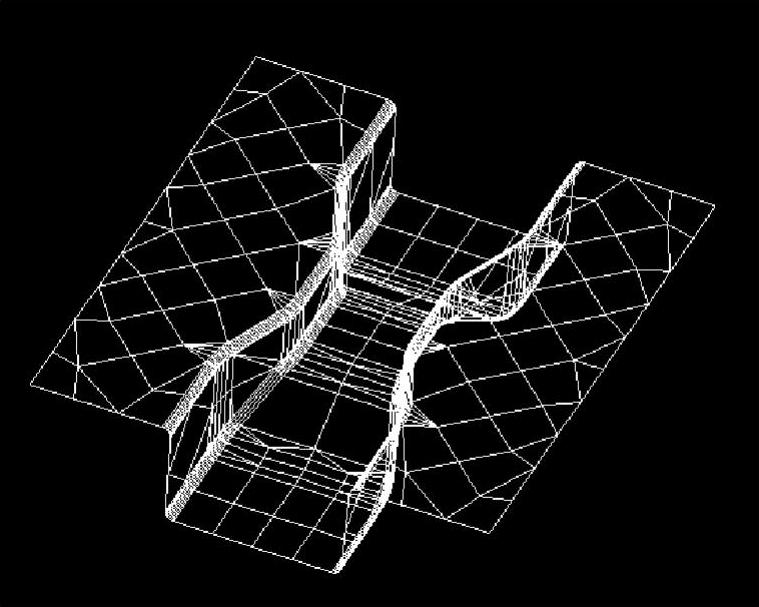
图5-11 模具型面网格
针对只有最终零件型面的分析算例，可在对零件型面（见图5-12）进行网格离散化后通过沿法向进行偏置得到凸、凹模的网格型面（见图5-13），由凹模型面偏置出凸模型面则间隙为-1.1t，而由凸模型面偏置出凹模型面则间隙为+1.1t，t为板料厚度。
(www.xing528.com)
图5-12 零件型面
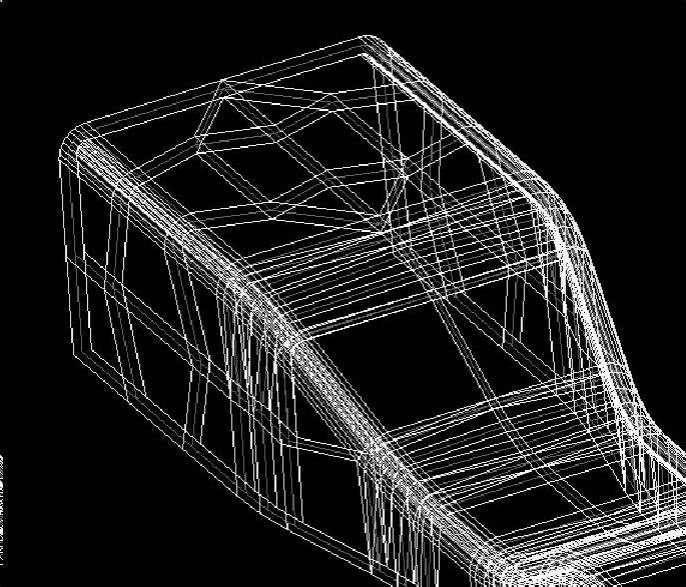
图5-13 由模具型面偏置出凸、凹模网格
在数值模拟过程中，计算精度和计算效率是一对矛盾。为了提高计算精度，需要增加单元的数目，对所研究的模型进行细化，这样就会导致计算成本的增加。而从计算效率的角度考虑，则希望单元数目越少越好，但单元数目的减少将导致计算精度下降，使计算结果失去意义。既满足计算的精度要求，又能保证较高的计算效率，人们提出了很多技巧和技术，其中，自适应网格技术得到了越来越多广泛的应用。
自适应网格方法是指在计算中，在某些变化较为剧烈的区域，如大变形、突出间断面、激波面和滑移面等，网格在迭代过程中不断调节，将网格细化，做到网格点分布于物理解的耦合，从而提高解的精度和分辨率的一种技术（见图5-14）。自适应网格希望在物理场量变动较大的区域的单元网格能够自动加密，而在物理场量变化平缓的区域的单元网格则相对稀疏，这样可在保持高效率的同时得到高精度的解。
图5-14 网格在零件圆角处产生自适应
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
