冲压成形模拟算法及稳定性分析

冲压成形过程是一个大变形的非线性力学过程，其数值分析以增量法为主，建立有限元格式的途径有两种，即T.L.法和U.L.法。可以证明，用这两种表达方式建立起来的有限元格式是等效的，如果采用与数学表达式一致的本构关系，它们将产生相同的结果。因此，无论是用T.L.格式还是U.L.格式，最终在经过有限元离散化之后建立起来的坯料运动方程都可以表示为

Mü+Cü+f＋f_i＝f_e （5-24）

式中 M、C——质量矩阵和阻尼矩阵；ü——节点位移矢量；

f_i、f_e——等效内力矢量和等效节点力矢量。

一般认为，冲压成形过程是一个准静力过程，因而速度和加速度的影响可以忽略。则考虑t时刻和t+Δt时刻的平衡方程为

f^t_i＝f^t_e （5-25）

f_i^t+Δt＝f_e^t+Δt （5-26）

以上两式相减，得到增量方程为

f_i^t+Δt-f^t_i＝f_e^t+Δt-f^t_e＝Δf_e （5-2

把f_i^t+Δt表示成u附近的仅保留线性项的Taylor展开式，可得到

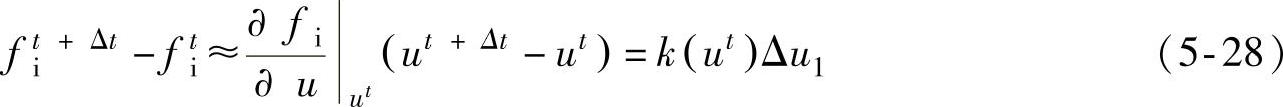
因而得到求解方程为

Δu₁＝k^-1（u^t）Δf_e （5-29）

u₁＝u^t+Δu₁ （5-30）

当Δf_e不大时，可以认为

u^t+Δt＝u₁ （5-31）

此刻为静力显式格式（Static Explicit Algorithm，SE）。

对于静力显式格式，为保证解的收敛性，必须严格限制增量Δf_e的大小。Δf_e的选择应满足以下条件：①任一单元的弹塑性状态在增量步内不发生变化；②任一主应变值的增量必须小于一给定值Δε_max，一般取Δε_max＝0.002；③任一旋转增量必须小于一给定值Δθ_max，一般取Δθ_max＝0.5°；④任一节点与模具表面的接触状态在增量步内不发生改变。材料弹塑性状态变化和接触状态变化在下一个积分步开始时加以考虑。

当步长Δf_e较大时，由于采用了近似表达式（5-28），造成由式（5-30）确定的u₁不满足平衡方程式（5-27），记此不平衡力为ΔR，则

f_i（u^t+Δt）-f_i（u₁）＝ΔR （5-32）(www.xing528.com)

把f_i（u^t+Δt）表示成u₁附近的仅保留线性项的Taylor展开式，得到

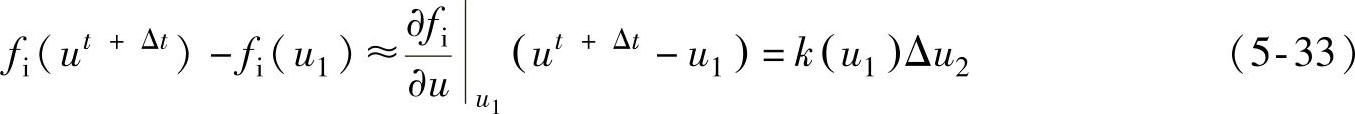
从而得到新的近似解为

Δu₂＝k^-1（u₁）ΔR （5-34）

u₂＝u₁+Δu₂ （5-35）

重复以上步骤，直至ΔR足够小，则可得到t+Δt时刻的解u^t+Δt。此即为静力隐式格式（Static Implicit Algorithm，SI）。ΔR→0是此格式的收敛判据。

如果在式（5-26）中也考虑速度和加速度的影响，相当于把冲压成形过程看做一个在动载荷作用下的力学响应过程。采用适当的处理方法，M和C可以转化为对角阵。考虑t时刻的运动方程，由中心差分算法可得到在t+Δt时刻的节点位移u^t+Δt为

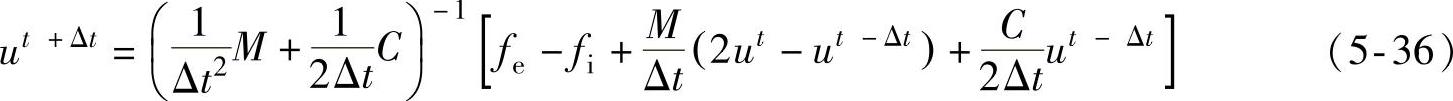
此即动力显式格式（Dynamic Explicit Algorithm，DE），每个自由度的位移可由式（5-36）独立求出。由于中心差分算法是条件稳定的积分算法，所以为保证式（5-36）的计算稳定性，时间步长Δt应满足

式中 T_min——有限元系统的最小固有振动周期。

从上述三种求解格式的求解过程来看，静力隐式格式在每一增量步内都要进行多次迭代，直至满足收敛性条件后，再进入下一增量步；一旦某一步收敛条件不满足，则将导致收敛性错误而停止运算，得不到所需的解答，因而当模型较大、单元数目较多时，静力隐式格式的计算时间将相当长。

起初人们都采用静力隐式格式有限元来分析冲压成形问题，因为当时分析的都是简单几何形状模具下的成形，如轴对称等二维问题，相应的模型比较小，在这种情况下静力隐式格式比动力显式格式的计算效率高（因为动力显式格式受最小时间步长的限制），而且由于接触状况等边界条件都很简单，收敛性条件很容易被满足，所以静力隐式格式有限元受到了普遍关注，得到了很大的发展。当人们把静力隐式格式有限元应用于分析覆盖件冲压成形问题时，遭遇了严重的计算效率和收敛性问题，因此人们把目光转向了显式格式有限元。

静力显式格式有限元把每一增量步限制得非常小，而且认为在每一增量步内单元的弹塑性状态和接触状态不发生改变，在每一增量步内不必经过迭代，因而避免了收敛性问题。但是，与静力隐式格式有限元相比，静力显式格式有限元的计算效率并没有多大改善。

动力显式格式有限元不必构造和计算总体刚度矩阵，不必经过迭代，因而不存在收敛性问题，也不必因求解大量繁琐的线性化方程组而降低效率，所以它能够高效、稳健地获得所求解。虽然动力显式格式是条件稳定的，受最小时间步长的限制，但却可以利用这个最小时间步长限制来方便而有效地处理接触问题，因为对于接触问题而言，接触状态变化越小越容易处理。动力显式格式有限元的这些优势尤其是在处理像车身覆盖件这样的冲压成形问题时表现得更为明显。图5-9反映了动力显式格式有限元和静力隐式格式有限元的计算时间与分析模型大小的关系。

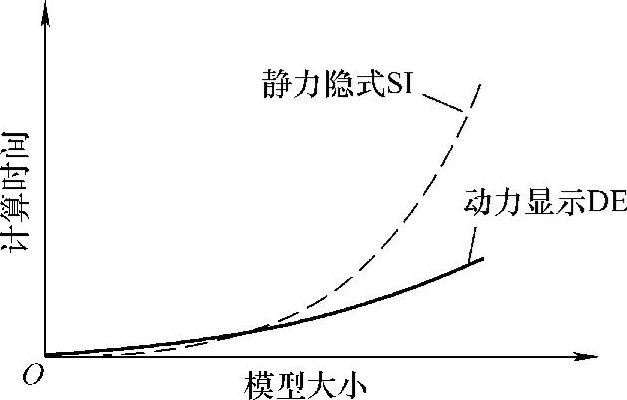
图5-9 DE和SI计算效率的比较

用动力显式格式有限元分析冲压成形问题也存在着不足之处：①把作为准静力过程的冲压成形问题处理成动力学过程，可能会引起解的精度偏差；②为了提高计算效率，不得不提高凸模速度，即所谓速度放大假设（Velocity Amplification Assumption），这可能在某些情况下造成不真实的解。但大量的研究表明，在一般情况下，用动力显式格式有限元分析冲压成形问题所获得的结果是合理的。