如何进行有限元仿真中的破裂判据优化？

在变形达到材料所能承受的极限后，材料就会发生破裂。由于有限元模拟中无法像实际情况中那样观察到零件的破裂，因此一个合理的破裂判据对有限元仿真来说极其重要。

几十年来很多学者分别采用宏观的连续介质力学方法和微观的损伤力学方法对成形极限进行理论研究，取得了很多研究成果，概括起来可以分为以下几类：第一类是经典的分叉理论，如Swift分散性失稳理论和Hill集中性失稳理论等；第二类认为材料局部初始不均匀性是导致缩颈的原因，如M-K理论等；第三类认为材料的局部细微裂纹是导致塑性失稳的原因，如损伤理论等。第一类理论是基于均匀连续体的失稳假设；后两类理论是基于非均匀材料的损伤失稳假设，将材料损伤的发生、发展引进失稳模型，建立修正判据。

但是以上理论方法在实际应用中尚存在很多困难，目前在商业化的有限元仿真软件中一般都采用基于经验公式的成形极限图（Forming Limit Diagram，FLD），这一概念最早由Kee-ler和Goodwin在1965年提出，后来通过进一步发展试验技术，由Goodwin于1968年进行补充，形成如今人们熟知的FLD图形式。

目前在板料成形的数值模拟中，用FLD（成形极限图）方法来预测破裂最为常见。模拟软件中通常采用经验公式（式5-23）获得FLD，只需输入材料的硬化指数n、厚度t和厚向异性系数R即可得到成形极限图，该经验公式可对普通钢板的破裂作出有效预测，但是对于一些高强钢，其准确性还有待验证。通过零件上应变点在成形极限图中的分布位置，可以对零件的成形质量作出判断（见图5-8）。

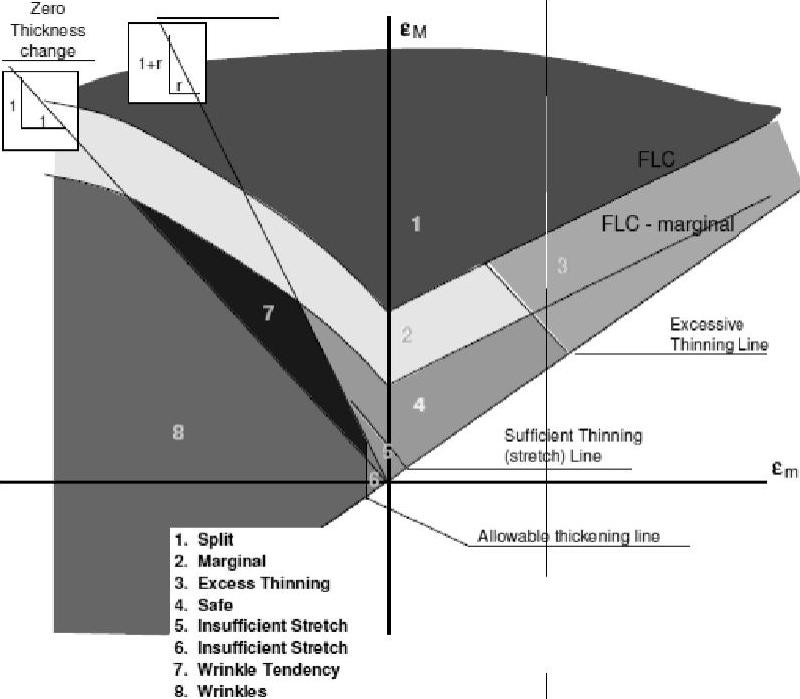
图5-8 成形极限图的应用(www.xing528.com)

FLD₀＝n（23.3+14.134t）/21.0 0＜;t＜;2.54mm

FLD₀＝n[20.0+（20.669-1.938t）t]/21.0 2.54≤t≤5.33mm

FLD₀＝75.125n/21.0 t≥5.33mm （5-23）

ε_maj＝FLD₀+ε_min（0.027 254ε_min-1.1965） ε_min＜0

ε_maj＝FLD₀+ε_min（-0.008 565ε_min+0.784854）ε_min＞0