材料强化模型：考虑各向异性与反向加载

塑性硬化法则规定了材料进入塑性变形后的后继屈服函数。此函数不仅与应力状态有关，还与塑性应变和强化参数有关。对于理想弹塑性材料，因无硬化效应，其屈服面是固定不变的。但对于用于汽车覆盖件冲压成形的板料，其在塑性屈服后将表现出较明显的强化效应，屈服面将随着塑性变形的发展而变化。

常用的材料强化模式有三种：各向同性强化、线性随动强化和混合强化（见图5-5）。

1.等向强化

等向强化即各向同性强化，是指无论在哪个方向加载，拉伸屈服极限同压缩屈服极限总相等，材料发生相同程度的强化，如图5-6所示。

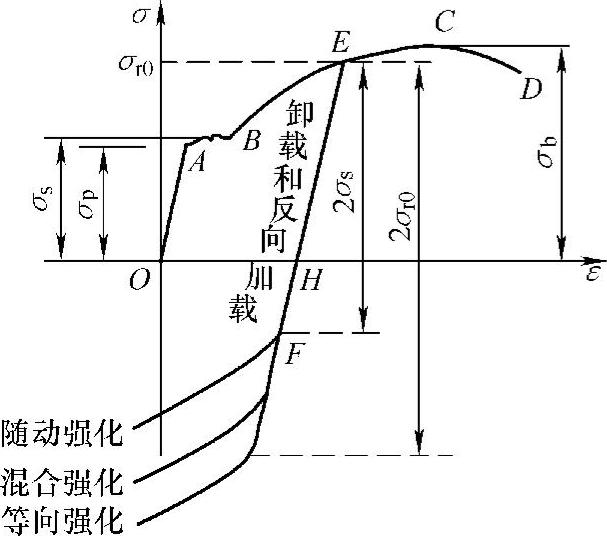
图5-5 三种强化模式

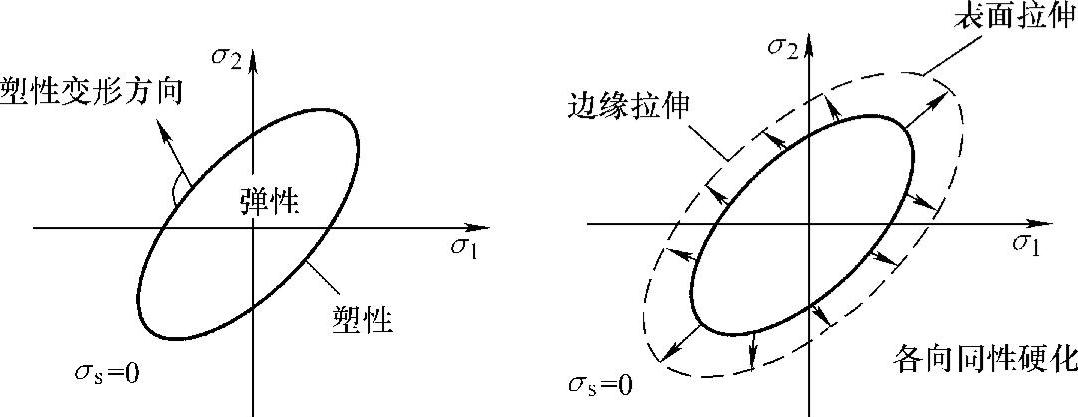
图5-6 等向强化示意图

此法则规定材料进入塑性变形以后，屈服面在各方向均匀地向外扩张，其形状、中心及其在应力空间的方位均保持不变。在这种情况下，后继屈服函数与初始屈服函数具有相同的表达形式。

等向强化的屈服面以材料中所做塑性功的大小为基础，在形状上作相似的扩张。对Mises屈服准则来说，屈服面在所有方向上均匀扩张。加载面仅由其曾经达到过的最大应力点决定，与加载历史有关。由于等向强化，在受压方向的屈服极限等于受拉过程中所达到的最高应力。

2.随动强化

随动强化产生包申格效应，随着塑性变形的增加，屈服极限在一个方向上提高而在相反方向上降低的效应即为包申格效应，此时材料为各向异性。若一个方向的屈服极限提高的数值和相反方向屈服极限降低的数值相等，则称为理想的包申格效应，此时材料的强化现象称为随动强化，如图5-7所示。

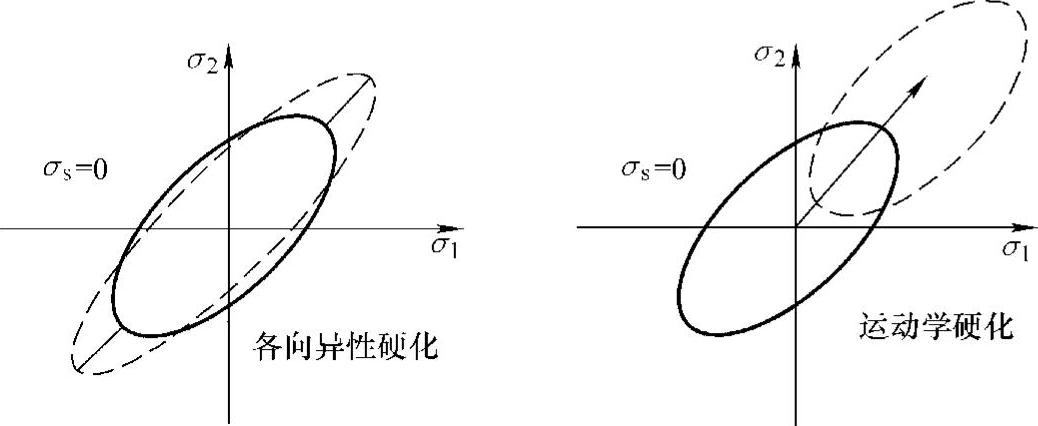
图5-7 各向异性硬化及随动强化图

此法则规定材料进入塑性变形以后，屈服面在应力空间作刚体移动，而其形状、大小和方位均保持不变。在这种情况下，后继屈服面可表示为

Φ（σ_ij，α_ij）＝0 （5-18）

式中 α_ij——屈服面中心在应力空间的移动张量。

根据α_ij不同的规定，随动强化准则又有Prager运动硬化准则和Zeigler运动硬化准则两种形式。(www.xing528.com)

随动强化理论中包含包申格效应，认为对大多数金属来说，假定屈服面的大小保持不变而仅在屈服的方向上移动，当某个方向的屈服应力增大时，其相反方向的屈服应力则降低。在随动强化中，由于拉伸方向屈服应力的增加导致压缩方向屈服应力的降低，所以在对应的两个屈服应力之间总存在一个2σ_s的差值，初始各向同性的材料在屈服之后将不再是同性的。相应的屈服函数表示为

F（σ_ij，α_ij）＝f（σ_ij-α_ij）-k＝0 （5-19）

式中 α_ij——移动张量，表示加载面中心的位移，它与塑性变形ε^p_ij的历程有关。

3.混合强化

混合强化即随动强化和等向强化同时存在。实验表明，弹塑性材料的屈服强化过程通常同时具有等向强化和随动强化特性，初始强化几乎完全是各向同性的，但随着塑性变形程度的增大，弹性域达到一定常数值，强化性质更接近纯运动状态。为了同时考虑这两种强化特性，提出了混合硬化的概念，其后继屈服函数表示为

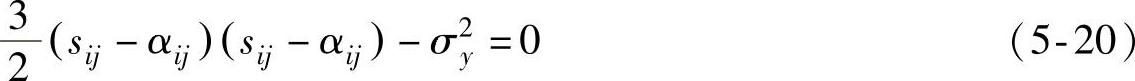
式中 α_ij、σ_y——ε^p_ij的函数，与塑性变形历程有关。

对于金属材料的应力应变曲线，研究学者们提出了多种表示方法。通常可以近似使用如下公式对材料的应变强化曲线进行逼近分析，即

σ＝Kεⁿ （5-21）

而在实际的数值分析中，常使用线性强化模型，通过双线性或多线性折线来表示应力应变曲线。对于双线性应力应变曲线，一般通过材料的弹性模量（弹性斜率）和切线模量（切线斜率）两个斜率来计算材料的塑性斜率。然后通过等效应力和等效应变进行分析计算。根据Mises屈服准则，屈服应力的计算公式为

σ_y＝σ_s+βE_pε_p （5-22）

式中 ε_p——等效塑性应变；

σ_s——初始屈服应力；

E_p——塑性硬化模量；

β——硬化参数（β＝1时为等向强化，β＝0时为随动强化，0＜β＜1时为混合强化）。

目前大部分有限元软件只包含各向同性强化和线性随动强化，对于混合强化模型的研究只限于线性混合强化模型。但超高强度钢在反向加载时具有很强的包申格效应，而在回弹模拟中考虑到包申格效应的影响是非常重要的，因为大多数汽车零件在冲压过程中包含了弯曲和非弯曲变形。在板料成形过程中，当材料流过模具圆角时经历严重的弯曲和反弯曲变形，引起塑性加载和卸载现象。在这种情况下，反向加载软化的模拟精度就成为影响回弹模拟精度的主要因素之一。采用现有的材料强化模型难以准确计算板料成形后横截面的应力，进而影响到板料回弹量的预测。因此，建立考虑板料反向加载过程中包申格效应的各向异性材料强化模型是准确预测超高强度钢冲压件回弹量的前提。