屈服准则的分类和应用

1.各向同性材料的屈服准则

1）Tresca在1864年首先提出了屈服准则的概念，他假定材料中的最大切应力达到一个临界值时材料发生屈服，后来Huber、Mises和Hencky发现静水压力对塑性变形没有贡献，分别独立地提出了屈服准则，这些准则表明弹性变形是导致材料从弹性变形到塑性变形的唯一因素。为了修正Tresca和Huber-Mises-Hencky屈服面的差异，Drucker在1949年提出了如下准则

ϕ＝J₂³-cJ²₃＝k² （5-3）

式中 J₂、J₃——应力偏量第二、第三不变量；

c、k——材料常数。

2）Hershey和Hosford于1972年在多晶体计算的一系列结果基础上，也提出了一个适用于各向同性材料的屈服准则，即

式中 m——与晶体结构有关的参数。

式（5-4）表示的准则在1979年被推广到平面应力条件下的各向异性材料，即Hosford（1979）屈服准则。

2.各向异性材料的屈服准则

（1）Hill屈服准则 为了描述各向异性材料的屈服面，1948年Hill在Huber-Mises_- Hencky准则的基础上引入系数，提出了Hill二次屈服准则，即Hill（1948）屈服准则。其平面应力状态下的形式为

式中 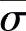——等效应力；

σ₁、σ₂——主应力；

R——厚向异性系数平均值。

Hill（1948）二次屈服准则是被最广泛使用的屈服准则，几乎所有的板料成形模拟程序均可以采用该准则进行计算，因为该准则可以用于复杂应力状态，并能推导出线性化的应力应变增量关系。Hill（1948）准则是各向异性塑性理论建立过程中的一个里程碑。它的表达式简单，应用方便，并能够较为准确地反映低碳钢的各向异性特征。后来许多屈服准则都是在该准则的基础上引入其他参数，获得了更高的计算精度。

Hill（1948）准则比较适合描述R值较高的材料的各向异性（如低碳钢），然而它在铝合金的应用中被证明是不适合的。其他非二次屈服准则，如Hill（1979、1990、1993）准则、Gotoh（1977）准则、Budianski（1984）准则、Weixan（1990）准则、Montheillet（1991）准则、Lin and Ding（1996）准则等可以更好地描述铝合金的屈服特征。

因为Hill（1948）屈服准则不能描述一些材料的“反常”行为（R＜;1），Hill在1979年提出了非二次屈服准则，根据系数的取值不同，它可以简化为四种特殊情况。如果假定面内主轴和各向异性主轴重合的话，Hill（1979）非二次屈服准则的一般形式可以考虑面内各向异性，但它的屈服面与多晶体模型导出的屈服面在某些情况下有较大的差异，Montheillet在1991年将其推广到更加一般的情况，提出了模型的精度。在四种特殊情况中，第四种是最常用的，它可以考虑厚向异性的影响，但是不能反映面内各向异性，其表达式为

在Bishop-Hill（1951）多晶体模型的基础上，Bassani在1997年提出了一个屈服准则，用来简化反映面内各向异性屈服面的形状。Hosford在1979年独立提出了如下屈服准则

式中 F、G、H——材料常数。

Hosford（1979）准则也可以看做Hill（1979）准则的推广，有的文献也将其作为Hill（1979）准则的第五种情况，其主要优点是可以通过调整m值，非常精确地逼近由多晶体Bishop-Hill模型得到的屈服轨迹。对于面心立方晶格的材料，取m＝6；对于体心立方晶格的材料，取m＝8～10。

Hill在1990年也在屈服准则中引入了剪切应力，即Hill（1990）准则，后来该准则经过局部修正，成为了Lin and Ding（1996）屈服准则。(www.xing528.com)

为了更精确地描述铝合金的变形行为，Hill在1993年提出了Hill（1993）准则，但只有在应力主轴和各向异性主轴平行的情况下方可使用。

（2）Barlat屈服准则Barlat及其合作者在Hosford屈服准则的基础上提出了一系列包含面内各向异性的屈服准则。Barlat and Lian（1989）屈服准则适合于平面应力状态，包含四个参数，是一种新的非二次屈服准则。Barlat and Lian（1989）屈服准则能更合理地描述有较强织构的各向异性金属板料的屈服行为，有效地模拟板料拉深成形过程中凸缘的塑性流动规律，可以模拟凸缘出现2、4、6个凸耳的现象，全面地反映了面内各向异性和屈服函数指数m对板料成形过程中的塑性流动规律及成形极限的影响。其函数形式为

式中 ；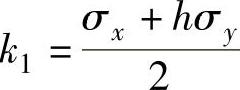

a、h、p——材料常数。

Barlat于1991年在各向同性Hershey-Hosford准则的基础上，通过用张量取代主应力的方法将其扩展到三维应力状态，并且引入了其他六个参数，得到了Barlat（1991）屈服准则。Lian和Chen也用了几乎相同的方法将Hill（1979）准则作了推广。Karafillis和Boyce在1993年提出了Karafillis and Boyce（1993）准则，该屈服函数考虑了两个凸函数的加权和，并通过一种线性应力变换引入各向异性。

Barlat在Barlat（1991）准则的基础上用线性应力变换推导出了包含7个参数的屈服函数——Barlat（1997）屈服函数。该屈服函数的缺陷是没有证明过屈服面的外凸性，而且由于它的形式过于复杂，很难在有限元中应用。Yoon（2000）准则和Barlat（2003）准则的出现补偿了这些不足，该屈服准则应用了两个线性应力变换，包含8个参数，而且它容易被证明是外凸的，目前已被应用在有限元模拟软件中。有关线性应力变换的内容在Aretz and Barlat（2004）准则和Barlat（2005）准则中有所阐述。从这个基本理论出发，Yoon在2005年提出了两种新的分别含有13个和18个参数的屈服方程，这些模型可以描述杯形件拉深时的6个或8个凸耳现象。

（3）其他的屈服准则 近年来，国际上又出现了不少新的屈服准则，Banabic等人提出了描述平面应力问题的含有6个参数的屈服准则——BBC（2000）准则和Banabic（2003）准则，事实上它也是Barlat and Lian（1989）准则的推广，这个屈服准则随后被改进为包含8个参数的Paraianu（2003）准则和Banabic（2003、2005）准则。

BBC（2000）准则应用于平面应力状态，其表达式为

式中 a、b、c、m——材料常数；

Γ、Ψ——应力张量第二和第三不变量的函数。

m的取值与材料有关：对于BBC材料，取m＝3，对于FCC材料，取m＝4。

2002年，Cazacu和Barlat拓宽了应力张量第二和第三不变量的含义，提出了CB2002准则，即

ϕ＝（J⁰₂）³-c（J⁰₃）²＝k² （5-10）

对于一般应力状态，该准则需要确定18个参数，对于平面应力状态也需要确定10个参数，因而应用较为困难。

Bron和Besson在2004年也提出了一种屈服准则，它结合了Karafillis and Boyce（1993）准则和Barlat（1991）准则。与Barlat（2003）准则一样，该准则采用了两个线性应力变换。

Vegter等人提出了Vegter（1999、2003、2006）准则，这些屈服准则与以上提到的屈服准则有显著不同的各向异性方程导出方式。在这里，平面应力状态由主应力表示，θ表示第一主轴与轧制方向的夹角，每个主应力平面由θ来确定，屈服轨迹是由一系列实验测得的应力点组成的二阶Bezier内插值方程；在每个主应力平面里，组成屈服轨迹的实验点由单向拉伸、平面应变、双向等拉和纯剪切测试所得到。在该模型中，可以纳入任意数目的θ平面，通过对θ的傅里叶级数展开实现一系列θ平面的内插值。

在经典的塑性理论中，仅在初始屈服状态用到建立本构模型的各向异性屈服方程，这样就不能将硬化带来的各向异性考虑进去，同时会导致后继屈服的各向异性对初始屈服状态非常敏感。因此，Weilong Hu在2007年提出了包含硬化的各向异性本构模型——Hu（2007）模型，该模型能更合理地描述轧钢等具有明显各向异性的材料的变形行为，且各向异性值会随着塑性应变的增大而减小。

归纳来说，常用来分析板料成形的屈服准则有：Hill（1948、1979、1993）准则、Edel-man and Drucker（1951）准则、Hershey（1954）准则、Hosford（1972、1979、1980、1996）准则、Bassani（1977）准则、Gotoh（1977）准则、Gupta（1977）准则、Bressan and Wil-liams（1983）准则、Budianski（1984）准则、Barlat and Lian（1989）准则、Barlat（1991、1993、2003）准则（即Yoon2000准则）、Karafillis and Boyce（1993）准 则、Banabic（2000）准则等。