盒形件的拉深制造技术优化方案

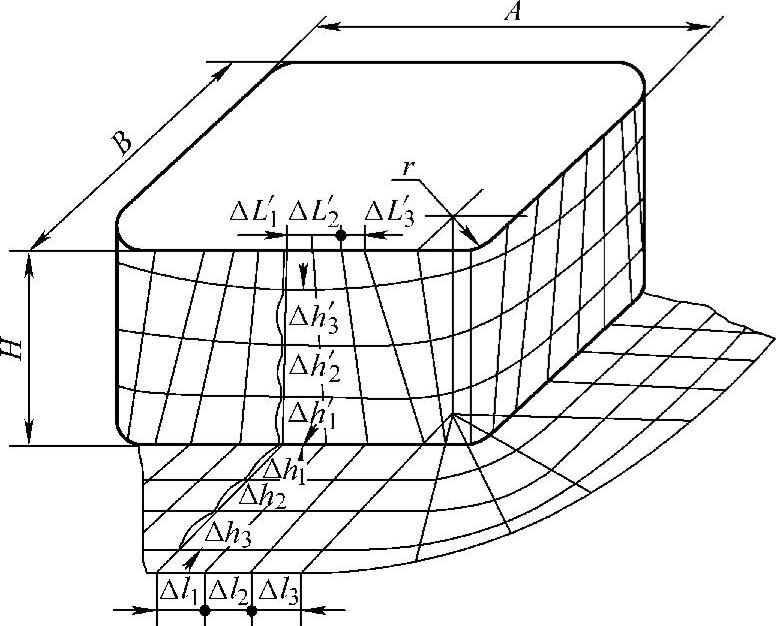
图3-145 盒形件的拉深变形特点

1.盒形件的拉深变形特点

盒形件属于非轴对称零件，它包括方形盒件、矩形盒件和椭圆形盒件等，从几何形状特点看，矩形盒状零件可划分成2个长度为A-2r和2个长度为B-2r的直边加上4个半径为r的1/4圆筒部分（见图3-145）。若将圆角部分和直边部分分开考虑，则圆角部分的变形相当于直径为2r、高为h的圆筒件的拉深，直边部分的变形相当于弯曲。但实际上圆角部分和直边部分是联系在一起的整体，因此盒形件的拉深又不完全等同于简单的弯曲和拉深，它有其特有的变形特点，这可通过网格试验进行验证。

拉深前，在毛坯的直边部分画出相互垂直的等距平行线网格，在毛坯的圆角部分，画出等角度的径向放射线与等距离的同心圆弧组成的网格。变形前直边处的横向尺寸是等距的，即ΔL₁＝ΔL₂＝ΔL₃，纵向尺寸也是等距的，拉深后零件表面的网格发生了明显的变化（见图3-145）。这些变化主要表现在：

（1）直边部位的变形 直边部位的横向尺寸ΔL₁、ΔL₂、ΔL₃变形后成为ΔL₁′、ΔL₂′、ΔL₃′，间距逐渐缩小，越向直边中间部位缩小越少，即ΔL₃′＜ΔL₂′＜ΔL₁′＜ΔL₁；纵向尺寸Δh₁、Δh₂、Δh₃变形后成为Δh₁′、Δh₂′、Δh₃′，间距逐渐增大，越靠近盒形件口部增大越多，即Δh₃′＞Δh₂′＞Δh₁′＞Δh₁。可见，此处的变形不同于纯粹的弯曲。

（2）圆角部位的变形 拉深后径向放射线变成上部距离宽、下部距离窄的斜线，而并非与底面垂直的等距平行线；同心圆弧的间距不再相等，而是变大，越向口部越大，且同心圆弧不位于同一水平面内。因此该处的变形不同于纯粹的拉深。

根据网格的变化可知盒形件拉深有以下变形特点：

1）盒形件拉深的变形性质与圆筒件一样，也是径向伸长，切向缩短。沿径向越往口部伸长越多，沿切向圆角部分变形大，直边部分变形小，圆角部分的材料向直边流动，即盒形件的变形是不均匀的。

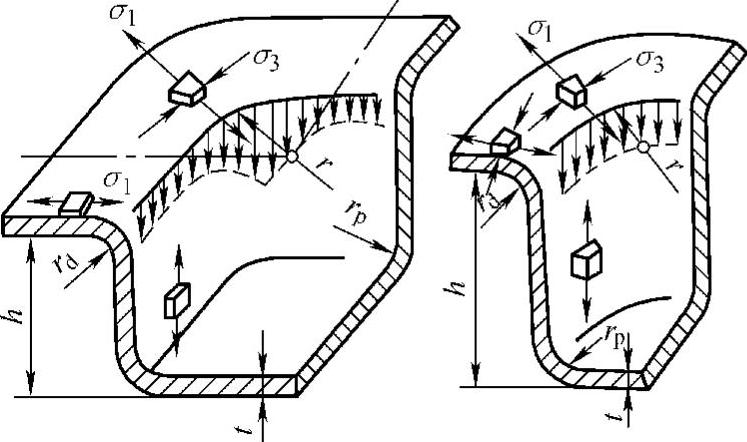
图3-146 盒形件拉深时的应力分布

2）变形的不均匀导致应力分布不均匀（见图3-146）。在圆角部的中点，σ₁和σ₃最大，向两边逐渐减小，到直边的中点处，σ₁和σ₃最小，故盒形件拉深时破坏首先发生在圆角处；又因圆角部材料在拉深时允许向直边流动，所以盒形件与相应的圆筒件比较，危险断面处受力小，拉深时可采用小的拉深系数，也不容易起皱。

3）盒形件拉深时，由于直边部分和圆角部分实际上是联系在一起的整体，因此两部分的变形相互影响：直边部分除了产生弯曲变形外，还产生了径向伸长、切向压缩的拉深变形。两部分相互影响的程度随盒形件相对圆角半径r/B和相对高度H/B（B为盒形件的短边长度）的不同而不同。

2.盒形件一次拉深的极限变形程度

r/B越小，圆角部分的材料向直边部分转移越多，直边部分对圆角部分的影响越大，极限变形程度的提高越显著；反之，r/B越大，直边部分对圆角部分的影响越小，而且当r/B＝0.5时，直边不复存在，盒形件成为圆筒形件，其极限变形程度也必然等于圆筒形件的极限变形程度。

H/B越大，圆角部分对直边部分的影响就越大，直边部分的变形与简单弯曲的差别就越大。

盒形件能否一次拉深的成形极限，可以用最大成形相对高度H_max/r表示，它取决于盒形件的尺寸r/B、t/B和板料的性能，其值见表3-48。当盒形件的相对厚度较小（t/B﹤1%），且A/B≈1时，取表3-48中较小值；当盒形件的相对厚度较大（t/B﹥1.5%），且A/B≥2时，取表3-48中较大值。表3-48中的数值主要适用于软钢板拉深。

表3-48 盒形件一次拉深的最大成形相对高度H_max/r

假若盒形件的相对高度H/r小于表3-48中的H_max/r，则盒形件可以一次拉成，否则需要采用多道工序拉深成形。

3.盒形件拉深毛坯的形状与尺寸的确定

盒形件毛坯的形状和尺寸必然与r/B和H/B的值有关。对于不同的r/B和H/B，盒形件毛坯的计算方法和工序计算方法也就不同。毛坯形状和尺寸计算的原则仍然是保证毛坯的面积等于加上修边量后的工件面积，并尽可能要满足口部平齐的要求。一次拉深成形的低盒形件与多次拉深成形的高盒形件，计算毛坯的方法是不同的。下面主要介绍这两种零件毛坯的确定方法。

（1）一次拉深成形的低盒形件毛坯的计算 低盒形件是指一次可拉深成形，或虽两次拉深，但第二次仅用来整形的零件。这种零件拉深时仅有少量材料从角部转移到直边，即圆角与直边间的相互影响很小，因此可以认为直边部分只是简单的弯曲变形，毛坯按弯曲变形展开计算。圆角部分只发生拉深变形，按圆筒形拉深展开，再用光滑曲线进行修正即得毛坯，如图3-147所示。

计算步骤如下：

1）按弯曲计算直边部分的展开长度l₀。

l₀＝H＋0.57r_p

H＝H₀＋ΔH （3-74）

式中 H₀——工件高度（mm）；

ΔH——盒形件修边余量（见表3-49）。

2）把圆角部分看成是直径为2r、高为h的圆筒形件，则展开的毛坯半径为

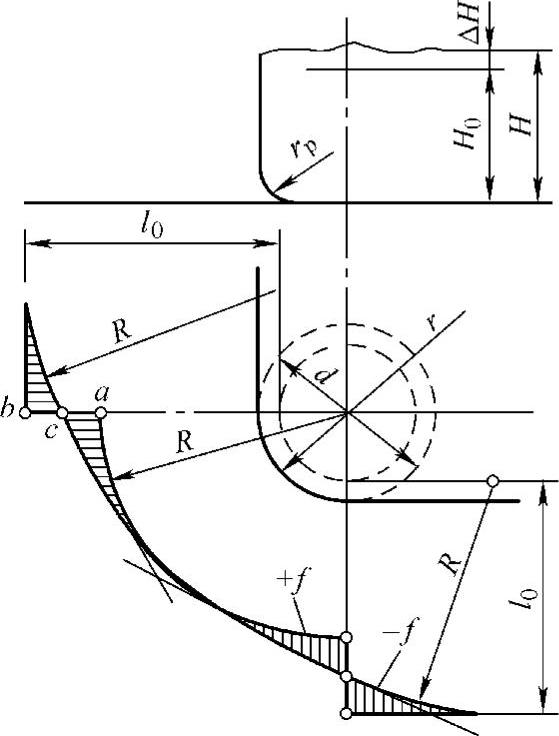
图3-147 低盒形件毛坯的作图法

3）通过作图用光滑曲线连接直边和圆角部分，即得毛坯的形状和尺寸：从ab线段的中点c向圆弧R作切线，再以R为半径作圆弧与直边及切线相切，使阴影部分面积＋f≈-f，这样修正后即得毛坯的外形。

表3-49 盒形件修边余量ΔH(www.xing528.com)

（2）高盒形件毛坯的计算 当零件为方形件（A＝B），且高度比较大，需要多道工序拉深时，可采用圆形毛坯，其直径为

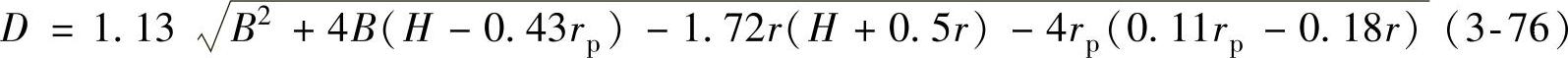
式（3-76）中的符号如图3-148所示。

对高度和圆角半径都比较大的盒形件（H/B为0.7～0.8），拉深时圆角部分有大量材料向直边流动，直边部分拉深变形也大，这时毛坯的形状可做成长圆形或椭圆形，如图3-149所示。将尺寸为A×B的矩形件，看做由两个宽度为B的半方形盒和中间为A-B的直边部分连接而成，这样，毛坯的形状就是由两个半圆弧和中间两平行边所组成的长圆形，长圆形毛坯的圆弧半径为

R_b＝D/2

式中 D——宽为B的方形件的毛坯直径，按式（3-76）计算，圆心距短边的距离为B/2。

则长圆形毛坯的长度为

L＝2R_b＋（A-B）＝D＋（A-B） （3-77）

长圆形毛坯的宽度为

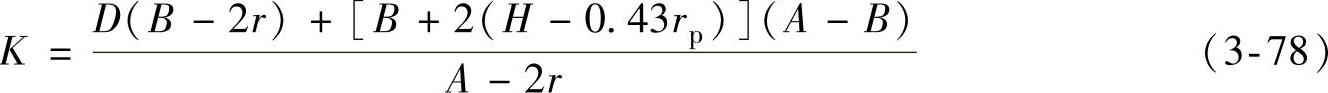
然后用R＝K/2过毛坯长度两端作弧，既与R_b弧相切，又与两长边的展开直线相切，则毛坯的外形即为一长圆形。

图3-148 高方形件毛坯的形状与尺寸

图3-149 高矩形件的毛坯形状与尺寸

4.高盒形件多工序拉深方法及工序件尺寸的确定

（1）高方形件的多次拉深 图3-150所示为多工序拉深方形件各中间工序的半成品形状和尺寸的确定方法。采用直径为D的圆形板料，每道中间工序都拉成圆筒形件，最后一道工序得到成品方形件的形状和尺寸。计算由倒数第二道（即n-1道）开始。n-1道工序所得半成品的直径计算式为

D_n-1＝1.41B-0.82r＋2δ （3-79）

式中 D_n-1——n-1道拉深工序后半成品的直径（mm）；

δ——角部壁间距，为n-1道工序半成品内表面到方形件内表面在圆角处的距离（mm）。

δ值对拉深时毛坯变形程度的大小，以及变形分布的均匀程度有直接影响。工件的r/B大，则δ小；拉深次数多时δ也小。过大的δ值可能使拉深件被拉裂。一般取δ＝（0.2～0.25）r。

图3-150 方形件拉深的半成品形状与尺寸

n-1道直径确定后，其他各道工序可按圆筒形件拉深的计算方法确定，即由直径D的平板毛坯拉深成直径为D_n-1、高为H_n-1的圆筒形件。

（2）高矩形件的多次拉深 这种拉深可采用图3-151所示的中间毛坯形状与尺寸。可把矩形盒的两个边视为4个方形盒的边长，在保证同一角部壁间距离δ时，可采用由4段圆弧构成的椭圆形筒，作为最后一道工序拉深前的半成品毛坯（是n-1道拉深所得的半成品）。其长轴与短轴处的曲率半径分别用R_a（n-1）及R_b（n-1）表示，计算式为

R_a（n-1）＝0.707A-0.41r＋δ，R_b（n-1）＝0.707B-0.41r＋δ（3-80）

圆弧R_a（n-1）及R_b（n-1）的圆心可按图3-151的关系确定。得出n-1道工序后的毛坯过渡形状和尺寸后，应检查是否可能用平板毛坯一次冲压成n-1道工序的过渡形状和尺寸，如果不可能，便要进行n-2道工序的计算。n-2道拉深工序把椭圆形毛坯冲压成椭圆形半成品，这时应保证

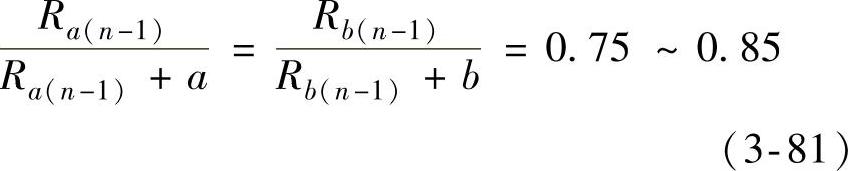
式中 a、b——椭圆形过渡毛坯之间在长轴和短轴上的壁间距离（mm）。

得到椭圆形半成品之间的壁间距离a和b之后，可以在对称轴线上找到两交点M和N，然后选定半径R_a和R_b，使其圆弧通过M和N，并且又能圆滑相接。R_a和R_b的圆心都比R_a（n-1）及R_b（n-1）的圆心更靠近矩形件的中心点O。得出n-2道拉深工序的半成品形状和尺寸后，应重新检查是否可能由平板毛坯直接冲压成功。如果还不能，则应该继续进行前一道工序的计算，其方法与此相同。

由于矩形件拉深时沿毛坯周边的变形十分复杂，上述的各中间拉深工序的半成品形状和尺寸的计算方法是相当近似的。假若在试模调整时发现圆角部分出现材料堆聚，应适当减小圆角部分的壁间距离。

图3-151 矩形件拉深的半成品形状与尺寸