拉深过程的力学分析及尺寸确定

1.凸缘变形区的应力分析

（1）拉深中某时刻凸缘变形区的应力分布 拉深时，凸缘的应力状态为径向受拉应力σ₁，切向受压应力σ₃，厚度方向的压应力σ₂可忽略不计，则只需求σ₁和σ₃的值，即可知变形区的应力分布。

径向拉应力σ₁和切向压应力σ₃的大小为

式中 σ_m——变形区材料的平均抗力（MPa）；

R_t——拉深中某时刻的凸缘半径（mm）；

R——凸缘区内任意点的半径（mm）。

拉深毛坯凸缘变形区各点σ₁、σ₃的分布如图3-115所示。在变形区的内边缘（即R＝r处）径向拉应力σ₁取最大值，即

在变形区外边缘（R＝R_t处）切向压应力σ₃取最大值，即

从凸缘外边缘向内边缘σ₁由低到高变化，σ₃则由高到低变化，在凸缘中间必有一交点，σ₁＝|σ₃|，易由式（3-43）得：R＝0.6R_t，也就是说，半径为R的圆将凸缘变形区分成两部分，由此圆向凹模腔口方向的部分，拉应力占优势（σ₁＞|σ₃|），拉应变ε₁的绝对值最大，材料厚度是减薄的；由此圆向外到毛坯边缘的部分，压应力占优势（σ₃＞σ₁），压应变ε₃的绝对值最大，材料厚度是增厚的。交点处就是变形区在厚度方向发生增厚和减薄变形的分界点。

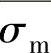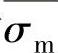（2）拉深过程中σ_1max的变化规律 由式（3-44）可知，σ_1max与变形区材料的平均抗力及表示变形区大小的R_t/r的乘积有关。随着拉深的进行，因加工硬化使逐渐增大，而R_t/r逐渐减小，但此时的增大占主导地位，所以σ_1max逐渐增加，大约在拉深进行到R_t＝（0.7～0.9）R₀时，σ_1max也出现最大值σ^max_1max。以后随着拉深的进行，由于R_t/r的减小占主导地位，σ_1max也逐渐减少，直到拉深结束（R_t＝r）时，σ_1max减少为零。

（3）拉深过程中|σ3|_max的变化规律 由式（3-45）可知，|σ3|_max仅取决于，只与材料有关，即随着拉深的进行，变形程度增加，σ_m增加，故|σ3|_max也增加。随着拉深的进行，变形程度增加会使毛坯有起皱的危险。

2.筒壁传力区的受力分析

凸模的压力F通过筒壁传递至凸缘的内边缘（凹模入口处），将变形区的材料拉入凹模（见图3-120）。显然，筒壁所受的拉应力主要是由凸缘材料的变形抗力σ_1max引起的，此外还有：

1）由于压边力F_Q在凸缘表面所产生的摩擦力，引起的摩擦阻力应力σ_M，其计算式为

式中 μ——材料与模具间的摩擦系数；

F_Q——压边力（N）；

d——凹模内径（mm）；

t——材料厚度（mm）。

图3-120 筒壁传力区的受力分析

2）凸缘材料流过凹模圆角时，产生弯曲变形的阻力引起的拉应力σ_W，其计算式为

式中r_d——凹模圆角半径（mm）；

R_m——材料的强度极限（MPa）。

3）材料流过凹模圆角后又被拉直成筒壁的反向弯曲力σ′_W，仍按式（3-47）进行计算，即

拉深初期，凸模圆角处的弯曲应力σ″_W也仿式（3-47）计算，即

式中 r_p——凸模圆角半径（mm）。

4）材料流过凹模圆角时的摩擦阻力，近似用摩擦阻力系数e^μα来进行修正，其中，α为包角（材料与凹模圆角处相接触的角度）。因此，筒壁的拉应力总和为

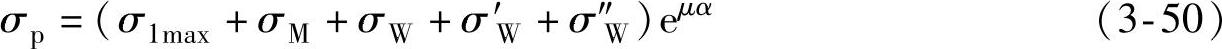
由式（3-50）知，σ_p在拉深中是随σ_1max和包角α的变化而变化的。当拉深中材料凸缘的外缘半径R_t＝（0.7～0.9）R₀时，σ_1max达最大值，此时包角α接近于π/2，则摩擦阻力系数为e^μπ/2，展开后略去高阶项，则近似为

故σ_p的最大值为

(www.xing528.com)

拉深中如果σ_pmax值超过了危险断面的强度R_m，则产生破裂。

3.毛坯形状和尺寸确定的依据

拉深时，金属材料按一定的规律流动，毛坯的形状必须适应金属流动的要求。实践证明旋转体零件的拉深可采用圆形毛坯。对于复杂形状的拉深件，通常都是先制造拉深模，根据分析，初步确定毛坯的形状，经多次试压和反复修改，直至符合要求后将毛坯形状最后确定下来，再做落料模。当然，毛坯轮廓的周边应圆滑过渡，不可有尖角或突变。

在不变薄拉深中，圆形毛坯的直径是按“拉深前后毛坯与工件的表面积不变”的原则来确定的。计算毛坯尺寸时，应以零件厚度的中线为基准来计算，即零件尺寸从料厚中间算起。

应当说明，拉深件毛坯受材料性能、模具几何参数、润滑条件、拉深系数以及零件几何形状等因素的影响，因此按上述原则确定毛坯尺寸时，应予以修正。

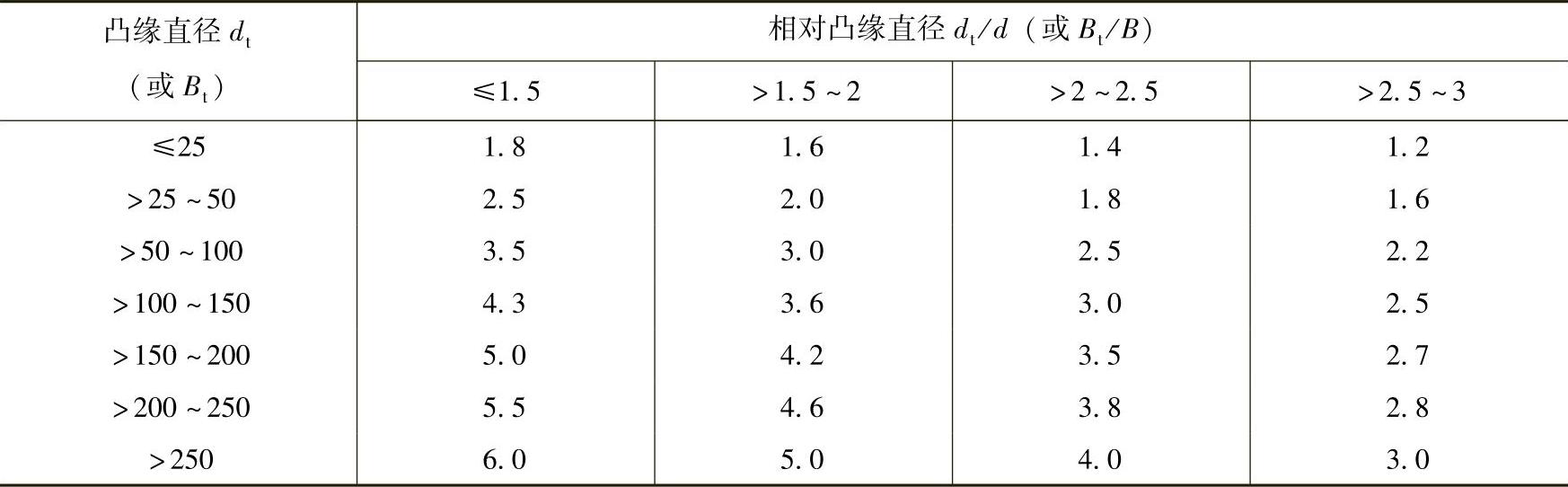
另外，由于材料的各向异性以及拉深时金属流动条件的差异，为了保证零件的尺寸，必须留出切边余量。在计算毛坯尺寸时，必须计入修边余量。修边余量见表3-35和表3-36。

4.简单旋转体拉深件毛坯尺寸的确定

求简单几何形状的拉深件的毛坯尺寸时，一般可将零件分解成若干个简单几何体，分别求出其表面积后，再相加，求出工件的总表面积。由于旋转体拉深件的毛坯为圆形，故可算出毛坯直径。拉深件的毛坯直径为

表3-35 无凸缘拉深件的修边余量（单位：mm）

注：1.B为正方形的边宽或长方形的短边宽度。

2.高拉深件必须规定中间修边工序。

3.对材料厚度小于0.5mm的薄材料作多次拉深时，应按表值增加30%。

表3-36 有凸缘拉深件的修边余量（单位：mm）

式中 D——毛坯直径（mm）；

A——包括修边余量在内的拉深件表面积（mm²）；

∑A_f——拉深件各部分表面积的代数和（mm²）。

图3-121所示的零件可看成由圆筒直壁部分（A₁），圆弧旋转而成的球台部分（A₂）以及底部圆形平板（A₃）三部分组成。

圆筒直壁部分的表面积为A₁＝πd（h＋δ）

圆角球台部分的表面积为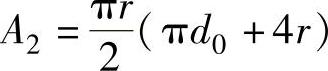

式中 d₀——底部平板部分的直径（mm）；

r——工件中线在圆角处的圆角半径（mm）。

底部表面积为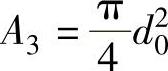

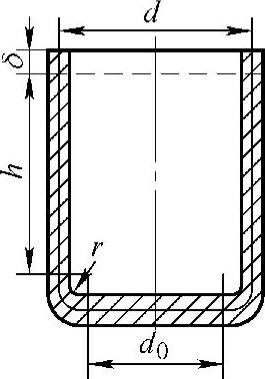
图3-121 圆筒零件毛坯尺寸的计算

将∑A_f＝A₁＋A₂＋A₃代入式（3-52）得

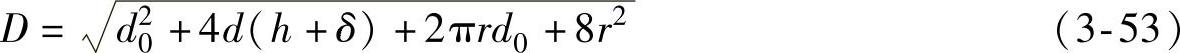
5.复杂旋转体拉深件毛坯尺寸的确定

对于各种复杂形状的旋转体零件，其毛坯直径的确定原则是：任何形状的母线绕轴旋转一周所得到的旋转体表面积，等于该母线的长度L与其重心绕旋转轴一周所得的周长2πR_s的乘积，即

式中 A——旋转体表面积（mm²）；

L——旋转体母线长度，其值等于各部分长度之和（mm），即L＝l₁＋l₂＋…＋l_n；

R_s——旋转体母线重心至旋转体轴的距离（mm）。

由式（3-52）得出毛坯直径为

式中 r_i——旋转体各组成部分母线的重心至旋转体轴的距离（mm）。