1.临界分切应力和晶体滑移系
导致晶体开始产生滑移,必须有一定的临界应力存在,试验证明不同取向(指晶体滑移方向和外力方向存在差异)的金属单晶体在不同的外加应力作用下开始滑移,但这些应力在滑移面和滑移方向上的分量也即临界分切应力是完全相同的(临界分切应力定律)。一般金属的临界分切应力为0.1~100MPa,具体数值和其纯度有很大关系。对于单晶体的单向拉伸,如图2-20a所示,外拉力P与晶体滑移面法向量之间的夹角为φ,与晶体滑移方向之间的夹角为λ,则临界分切应力τ与拉伸应力σ0之间的关系可表示为
τ=σ0 cos φcosλ
对于确定的金属材料,临界分切应力τ为常数,cosφcosλ定义为取向因子Ω,则σ0与Ω之间为反比例关系,试验结果与此很好地吻合,如图2-20b所示。在晶体内部,随着材料塑性变形的进行,外力与滑移面和滑移方向之间的夹角发生变化,取向因子Ω也发生变化。当取向因子逐渐减小时,需要的外力则逐渐增大,在到达一定程度后,该滑移系将停止运动。而金属材料的滑移系很多,在一个滑移系取向因子减小导致该滑移系逐渐趋于不利于运动的状态时,其他滑移系可能就转到有利于开动的位置而产生运动。一定阶段两个滑移系同样有利于开动时,就发生双滑移,还可能产生三滑移等。此外,两个相邻滑移系滑移方向相同而滑移面不同时,一定条件下可以产生交滑移,螺形位错在一定条件下可产生交滑移。通过多系滑移和螺形位错的交滑移以及刃形位错的攀移等,晶体内部产生相对运动。
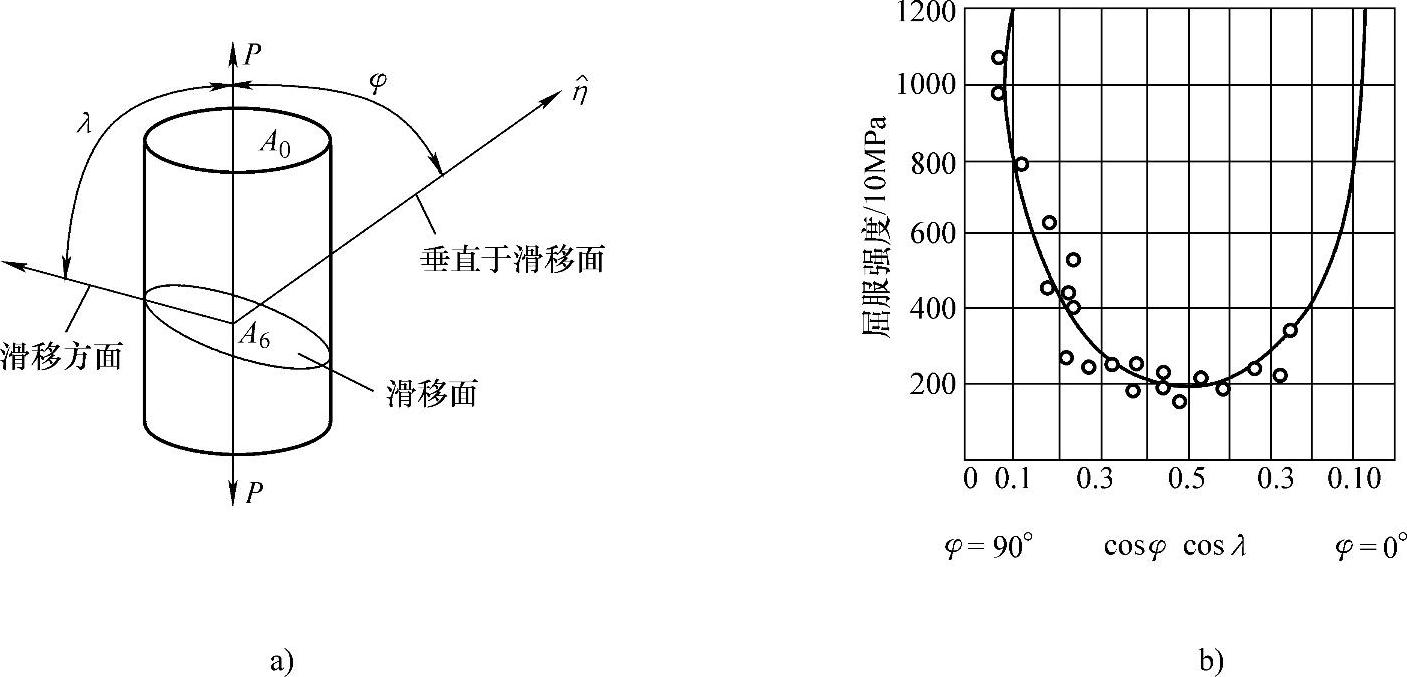
图2-20 材料临界分切应力和外力之间的关系
a)拉伸应力与临界分切应力之间的几何关系 b)镁晶体的屈服强度与晶体取向的关系
多晶体是由取向不同的许多小晶粒组成的。在外力作用下,有些晶粒处于有利取向,较易产生滑移;有些取向不利导致滑移困难。此外,每一晶粒的滑移难易程度还取决于临近晶粒的取向及晶界性质。滑移从一个晶粒过渡到相邻晶粒是困难的。多晶体中每个晶粒不可能只在取向最有利的一个滑移系上进行滑移,如果这样,在晶界处就要产生空隙。但实际上材料在变形过程中一直保持连续性,因而每个晶粒必须与邻近的晶粒产生协调变形,即形状能任意变化,这样就需要晶粒至少在五个独立的滑移系上进行滑移。多晶体是否具有塑性,首先要看它是否具备五个独立滑移系以保证各晶粒变形的协调性。
2.屈服强度
金属材料屈服是指材料发生永久性不可恢复变形,即塑性变形的开始。晶体的理论屈服强度为
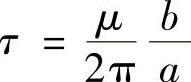
式中 τ——理论屈服强度;
μ——切变模量;
π——圆周率;
b——滑移方向的点阵周期;
a——原子层的间隔。
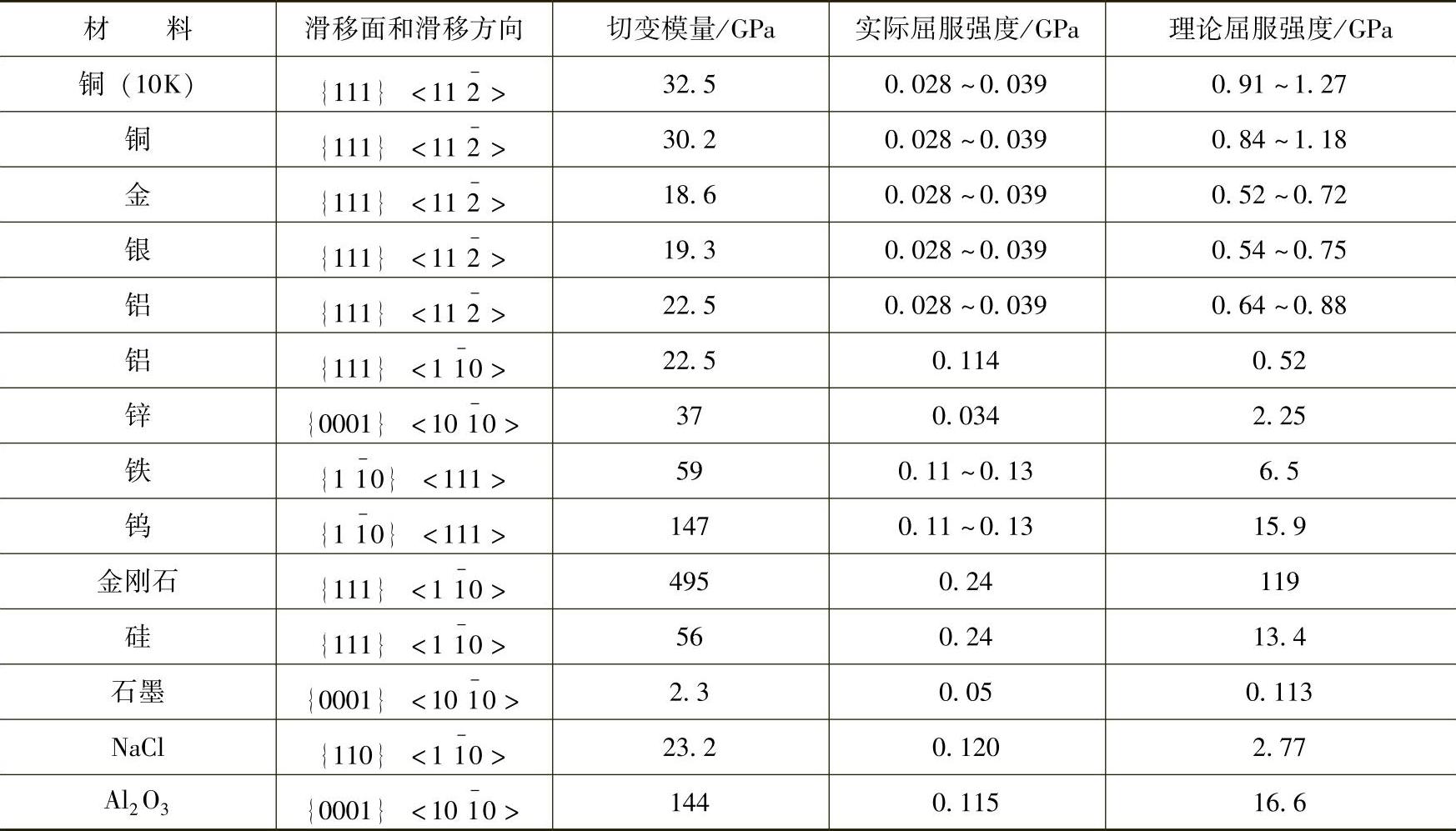
理论屈服强度的计算值见表2-5。
表2-5 几种元素的理论屈服强度的计算值
 (https://www.xing528.com)
(https://www.xing528.com)
然而,实际单晶体的临界分切应力随试样材料的纯度、位错密度等而变化,一般数量级为0.1~1GPa,比理论屈服强度低好几个数量级。这表明实际金属单晶体的屈服,不是原子面发生刚性滑移的结果,而是位错滑移的结果,因为金属晶体中位错在很低的应力作用下就可以运动。晶体的理论屈服强度标志着晶体屈服强度的上限,即晶体处于最硬状态(原子键合强度充分发挥作用的情况下)的屈服强度,它指出了各种强化金属方法的奋斗目标。晶体屈服强度的下限,即位错最容易运动情况下的屈服强度,就相当于晶体中其他缺陷全部被扫清以后使位错滑移所需的临界切应力,这就是位错的点阵阻力。
理论上提高金属强度有两条途径:第一,完全消除内部位错和其他缺陷,使它的强度接近于理论强度,例如无位错高强度的金属晶须,但这样的高强度不稳定,位错一旦产生,强度就大大下降;第二,在晶体中引入大量的缺陷,阻碍位错的运动,例如加工硬化、合金强化、细晶强化、组织强化、沉淀强化等,有效综合利用这些强化手段,也可以从另一方面接近理论强度,这是目前生产实践中广泛使用的方法。
3.屈服准则
材料某点的应力张量为对称二阶张量,可以表示为
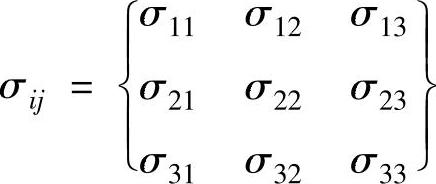
由切应力互等定理可知
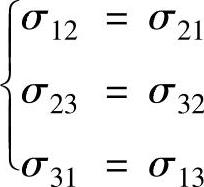 通过矩阵变换角度及旋转,σij可以用主应力表示为
通过矩阵变换角度及旋转,σij可以用主应力表示为
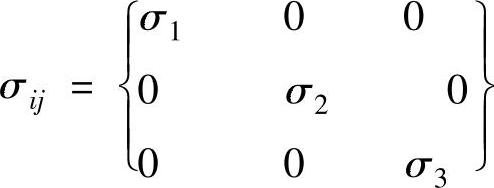
下面介绍材料的两个屈服准则。
(1)Tresca屈服准则 最大切应力达到某一数值时,材料进入屈服状态,表示为
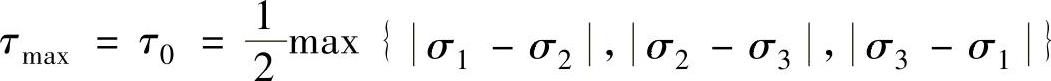
其中,τ0为最大切应力屈服值,等于简单拉伸屈服应力值的一半,即三个主应力中,两个主应力之差的最大值达到某一数值时,材料进入屈服状态。它表示主应力空间内与坐标轴成等倾斜的各边相等的正六角柱体,通常称为Tresca六角柱体。
(2)Von Mises屈服准则 与物体中一点的应力状态对应的畸变能达到某一数值时该点便屈服,以主应力表示的畸变能屈服条件为
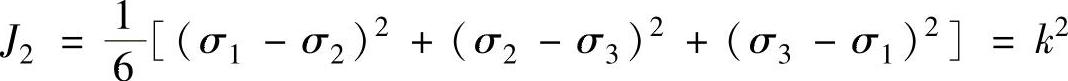
其中,k为表征材料屈服特征的参数,恒等于纯剪切应力状态时的最大切应力,与简单拉伸屈服应力σ0之间存在如下关系
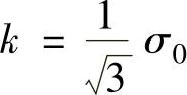
Von Mises屈服准则在主应力空间与坐标轴成等倾斜的圆柱体,进一步可证明,Von Mi-ses圆柱体外接于Tresca六角柱体。Tresca屈服准则和Von Mises屈服准则的几何表示如图2-21所示。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




