圆锥形件拉深时侧壁起皱失稳问题分析及优化建议

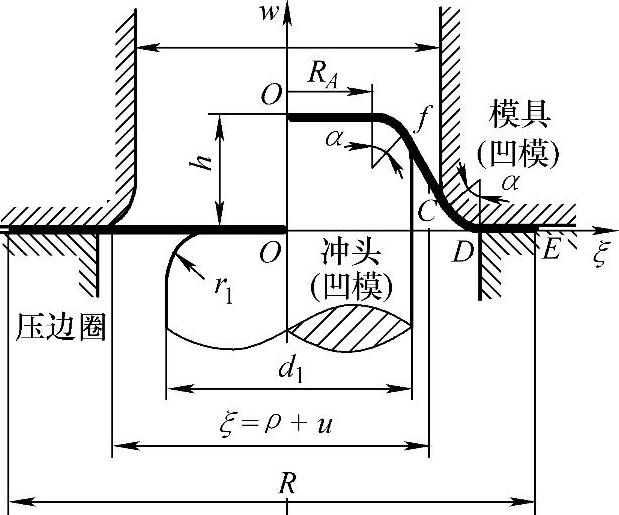
图1-29 圆锥形件拉深前后的几何关系

由于圆锥形件拉深成形中的悬空侧壁不与模具接触，因此防止侧壁起皱失稳通常是通过增大拉应力来相应地减小压应力实现的。从拉深试验结果和数值模拟来看，皱曲的最大挠度发生在距C点L/4～L/3处（L为悬空侧壁长度，见图1-29）。事实上，由于凹模圆角区对板料在拉深成形过程中的支撑作用，即拉深力F_P、压边力F_Q和压边圈、凹模共同作用，会对凹模圆角部分的板料产生一定的夹持作用，因而C处不容易成为圆锥形拉深件悬空侧壁部分的易起皱区。

基于以上分析可知，悬空侧壁某处在达到其压缩失稳极限后会屈曲失稳，而该处屈曲失稳后又势必影响其邻近区域。因此，对于悬空侧壁起皱失稳的研究，采用能量法求解能合理地给出悬空侧壁起皱失稳的判断依据。悬空侧壁起皱后能量变化主要表现为以下两个方面：

1）悬空侧壁起皱失稳后，由于C点和f点在几何上的限制，在纬向和经向都出现波纹隆起，其中纬向压应力因纬向缩短而做正功，经向拉应力因经向缩短而做负功。半波上边界应力所做的功记为ΔU^T。

2）悬空侧壁起皱后，波纹出现所引起的弯矩和扭矩都会消耗能量。半波的弯矩、扭矩所做的功记为ΔU^B。

由能量法可知，悬空侧壁起皱失稳的临界条件是

ΔU^T＝ΔU^B （1-232）

1.侧壁起皱数学模型

根据试验观察和数值模拟结果，可以得到图1-30所示的侧壁波纹示意图。设悬空侧壁的起皱波纹模型为

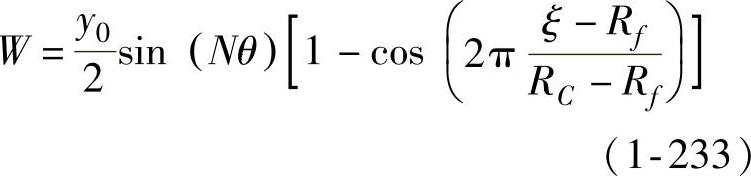
式中 R_f——拉深某瞬时应力分界圆半径；

R_C——质点C的径向半径；

ξ——悬空侧壁上任一质点的径向坐标；

N——悬空侧壁起皱时的波纹数；

θ——单波任意弧段所对应的圆心角，θ∈[0，π/N]；

y₀——单波最大波幅。

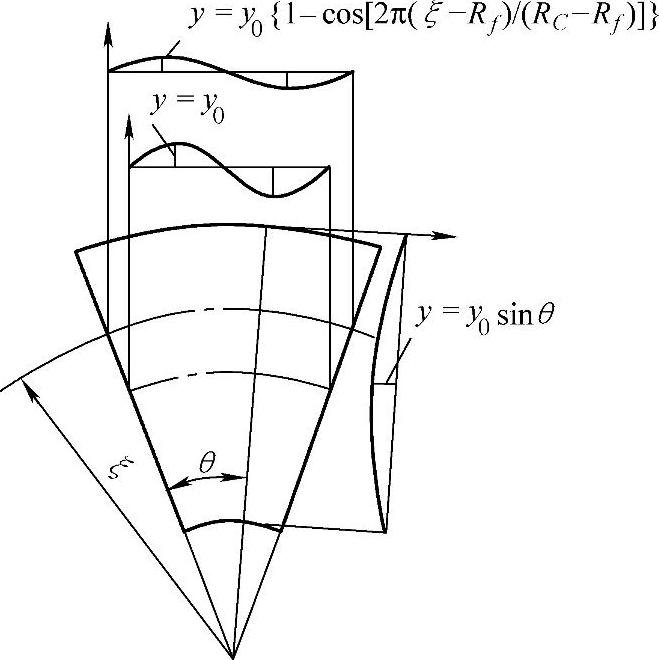
图1-30 侧壁波纹示意图

2.主应力分布规律

侧壁发生皱曲的拉深成形区的应力状态对应图1-31中的Ⅰ区。为简化推导过程，利用图示的特殊点连接而成的多边形来近似其外接椭圆，并用D、f两点的连线方程近似表示屈服方程，即

σ＝σ_r-K_σσ_θ （1-234）

式中 σ——等效应力。

设拉深力为F_P，假设悬空侧壁母线为直线，由轴向的力平衡可知

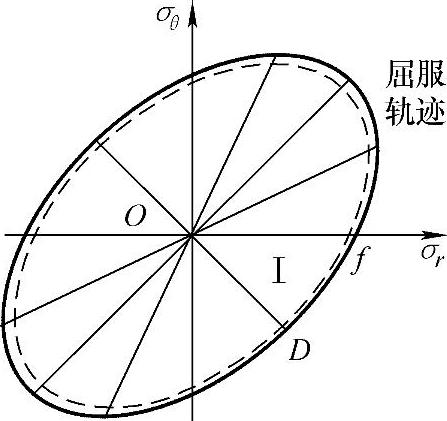
图1-31 侧壁发生皱曲的拉伸 成形区的应力状态对比

假设硬化规律满足

σ＝Bεⁿ （1-236）

式中 ε——等效应变；

B、n——强度系数和硬化指数。

将式（1-235）和式（1-236）代入式（1-234），可得纬向应力分布规律为

其中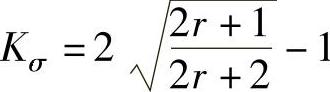，，r为各向异性参数。

假设板材成形过程中符合比例加载条件，由Hill各向异性流动方程可得

σ_ij＝L_ijklε_kl（i，j，k，l＝1，2） （1-238）

式中，L_ijkl——应力、应变之间的瞬时模量。有L₁₁₁₁＝L₁₁，L₂₂₂₂＝L₂₂，L₁₁₂₂＝L₁₂，其余根据假设均为零，其中

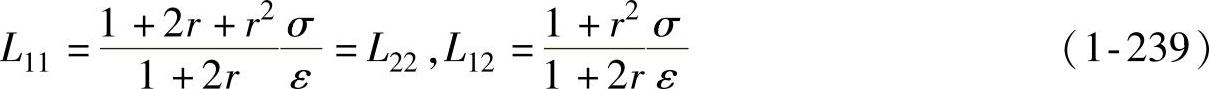
其中，σ按式（1-236）给出，ε按锥形件拉深侧壁变形区等效应变表达式给出，即(www.xing528.com)

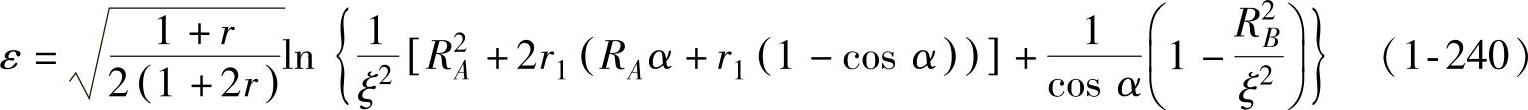
3.应力分界圆位置近似解

起皱失稳并非发生在全部存在压应力的成形区域，而是发生在起皱许可区。起皱失稳并非在fE区都发生，而是发生在fC区（内皱）和DE区（外皱），因此在侧壁皱曲分析过程中，应该首先确定f的位置（见图1-31），即确定应力分界圆的位置。

根据直母线假设和图1-29所示的几何关系可知

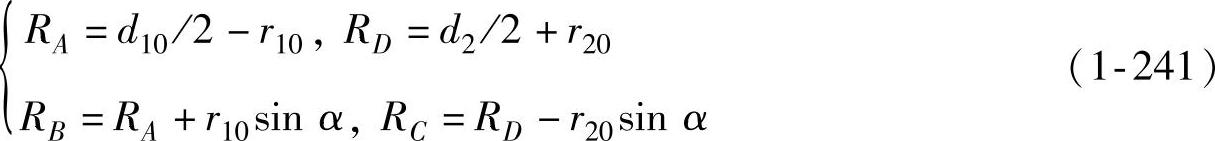
令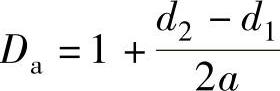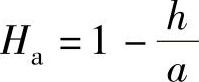，，a＝r₁₀＋r₂₀，则

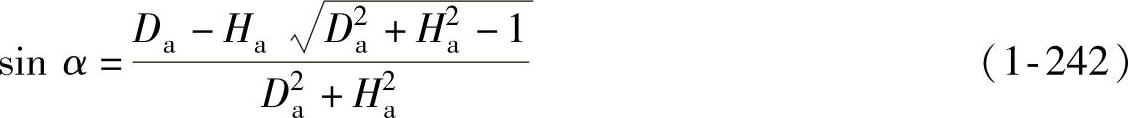
其中，r₁₀＝r₁＋t₀/2，r₂₀＝r2＋t0/2。

用理论方法求解R_f非常困难，但数值分析及试验研究表明，可以用近似公式（1-243）来确定f的位置，即

R_f＝2R_B/3＋R_C/3 （1-243）

4.侧壁起皱失稳的判断依据

在分析悬空侧壁起皱时，在此只考虑了塑性皱曲失稳。故在起皱分析过程中，仍采用悬空侧壁直母线假设，于是求出悬空侧壁中曲面的经向和纬向曲率分别为：b_r＝0，b_θ＝sinα/ξ。下面的计算过程对厚向异性的Hill修正屈服准则进行了线性近似简化，并采用Donnell-Mushtari-Vlasov（DMV）双曲薄壳模型给出了悬空侧壁的起皱失稳判断依据。

（1）ΔU^T值的计算 当皱纹出现后，假设悬空侧壁母线的长度不变，因而拉深力会因悬空侧壁同凸模相接处B点和悬空侧壁同凸模相接处C点直线距离的缩短而对皱曲的产生起负作用，纬向应力因周向缩短而做正功。皱曲出现后通过计算可得

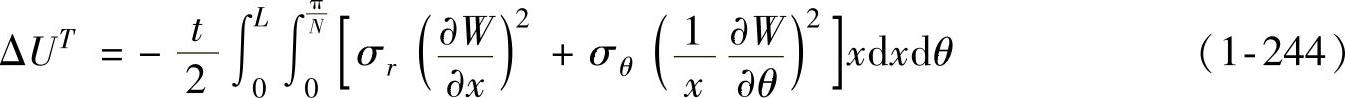
式中 L——直母线假设时悬空侧壁皱曲许可区母线方向长度，L＝（R_C-R_f）/cosα；

x——母线方向任意质点到应力分界圆的经向距离，x＝（ξ-R_f）/cosα。

（2）ΔU^B_w值的计算 为了求解方便，忽略因起皱产生的切应力。

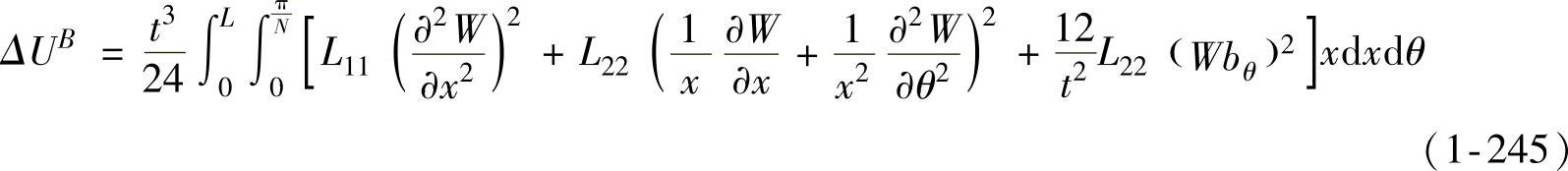
其中，L₁₁和L₂₂是应力应变之间瞬时模量张量，可根据式（1-239）求得；式（1-244）、式（1-245）的能量求解过程是基于（DMV）双曲薄壳模型给出的。

影响ΔU^B的有弯曲能和扭曲能，但主要是弯曲能，即皱曲后经向和纬向的波纹隆起引起的能量变化。试验结果表明，式（1-245）可以式（1-246）近似代替，即

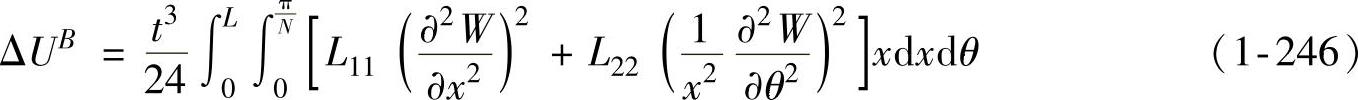
虽然式（1-246）的能量因素考虑少了，但因ΔU^B的减小，从而使得求解的临界成形力（也是临界压边力）增大了。从侧壁防皱基本原理来看，这样更安全，从实用角度来看也是合理的。

把式（1-233）、式（1-235）、式（1-237）、式（1-242）及L、x值代入式（1-244），再把式（1-233）、式（1-241）及L、x值代入式（1-246），然后根据式（1-232）可得悬空侧壁无皱临界拉深力的表达式为

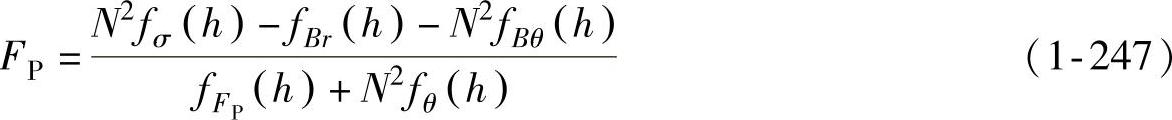
将式（1-247）对N微分，令∂F_P/∂N＝0，即可求得最小无皱拉深力下的N为

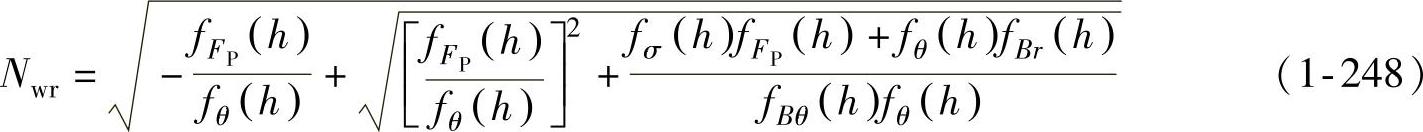
然后将N值代回式（1-247），即可得到悬空侧壁起皱的临界拉深力的理论计算公式为

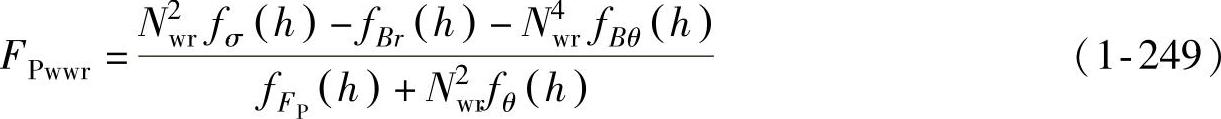
式（1-247）～式（1-249）中有

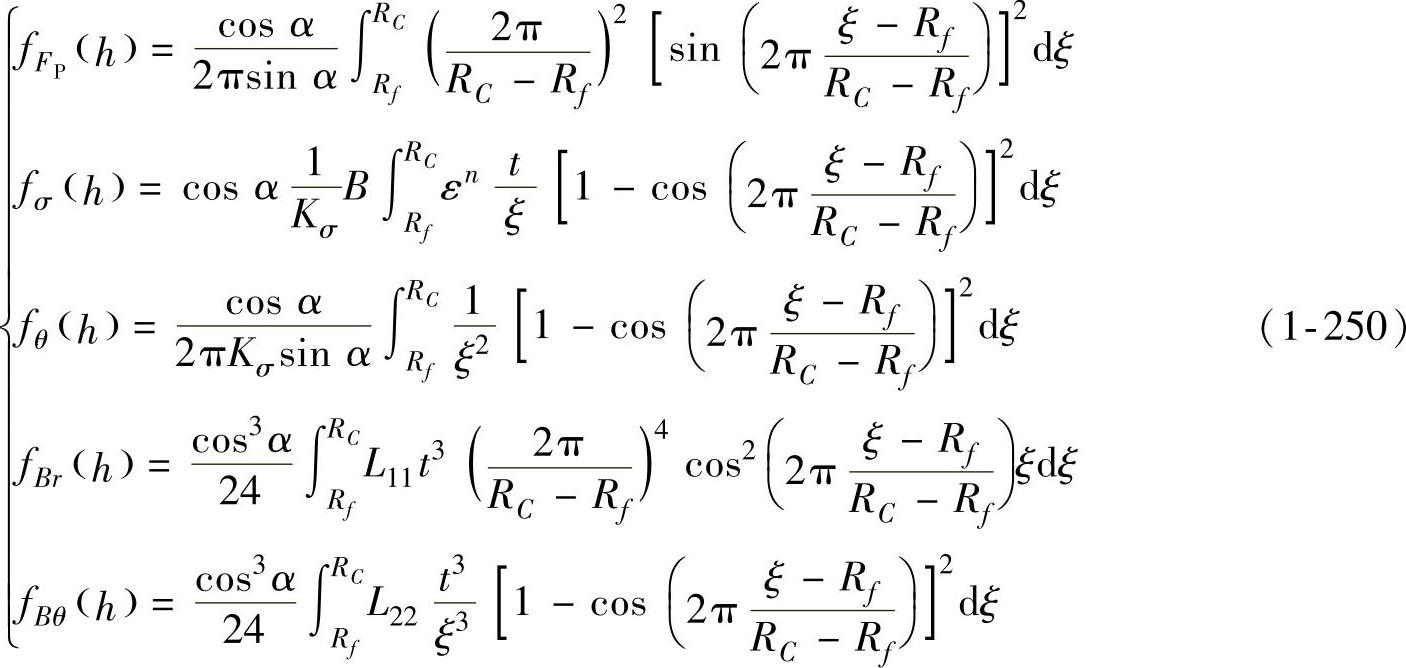
利用能量法导出了更为准确的拉深力和压边力的关系，悬空侧壁无皱临界压边力F_Qwwr为

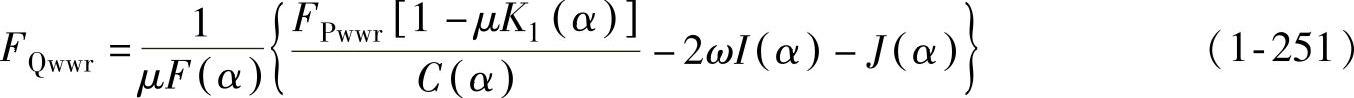
5.侧壁起皱临界压边力的实验验证

从式（1-248）和式（1-249）可以看出：侧壁起皱临界压边力随着成形高度的变化而变化，板材成形过程中的几何尺寸、材料性能参数（B，r，n）、润滑条件μ和毛坯相对厚度t₀/D₀都会影响侧壁起皱临界压边力。图1-32给出了侧壁起皱临界压边力的理论计算和试验结果的比较。试验用模具尺寸为D_d＝160mm、D_p＝128mm、r_d＝r_p＝8mm，材料为SPCC，毛坯尺寸D₀＝260mm、t₀＝0.7mm，材料性能参数B＝518.79MPa、n＝0.242、r＝2.07，摩擦系数μ＝0.2。

从图1-32可以看出，理论计算同试验结果的吻合程度良好。但在成形高度小于41mm时，同试验结果相比，理论计算偏大，这主要是由于等效应变解析不是十分准确而引起的。但从板厚均匀的要求来看，这样对成形更为有利。

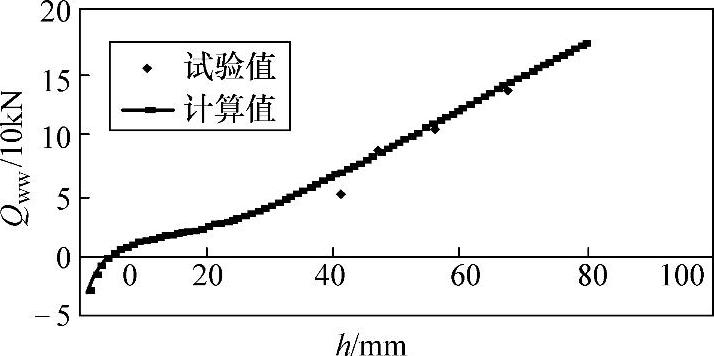
图1-32 侧壁起皱临界压边力的理论计算和试验结果的比较