如何解决法兰起皱失稳问题？

一般而言，法兰起皱时能量的变化主要有三个方面：

1）法兰失稳起皱，波纹隆起所需的弯曲功，设单波的弯曲功为U_w。

2）法兰失稳起皱后，周长缩短，切向应力因周长缩短而释出的能量，设单波释出的能量为U_θ。

3）波纹隆起时，压边力所消耗的功，设单波上压边力所消耗的功为U_Q。

在临界状态下，有

U_θ＝U_w＋U_Q （1-153）

以下分析中要用到切线模量D，其定义为硬化曲线的切线斜率，在此应提前给出。

设板材变形过程中等效应力与等效应变之间的关系与单向拉伸时的真实应力和真实应变之间的关系相同，符合Hollomon给出的指数硬化规律，即

σ＝Bεⁿ （1-154）

式中 B——板材的强度系数；

n——硬化指数，则

发生弹性弯曲时的弯矩公式为

发生塑形弯曲时的弯矩公式为

其中

式中 E——材料的弹性模量；

E_r——材料的折减模量。

1.筒形件无压边压延时的失稳临界条件（见图1-19）

（1）U_w假设—R为凸缘变形区的平均半径，b为凸缘宽度，失稳起皱后，皱纹的高度为δ，波形为正弦曲线，波纹数为N，则半波的长度l为

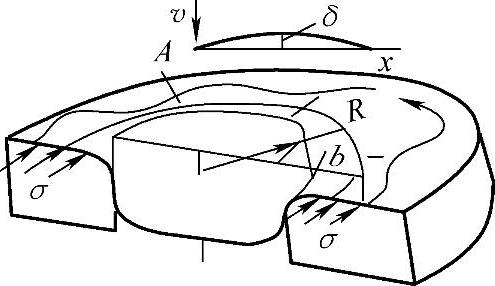
图1-19 压延时凸缘失稳起皱

若以坐标y表示任意点波纹的挠度，坐标x表示此点在半径—R的圆周上的投影位置，于是半波的数学模型可以表示为

材料力学中有关弹性弯曲的能量公式为

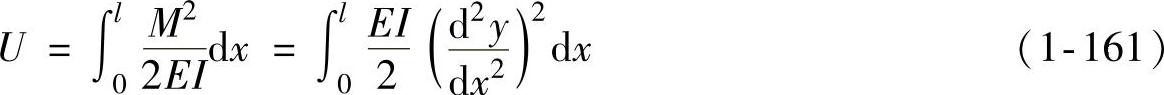
用折减模量E_r代替式（1-161）中的弹性模量E。假定切线模量D不变，则E_r为一常值。于是可以求得半波的弯曲功U_w为

将式（1-160）代入式（1-162），积分后可得

（2）U_θ凸缘失稳起皱后，周长缩短，半波的缩短量为

式中 dS、dx——半波微分段的弧长及其在x轴上的投影长度。又因

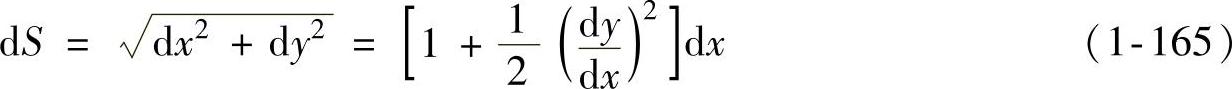
所以

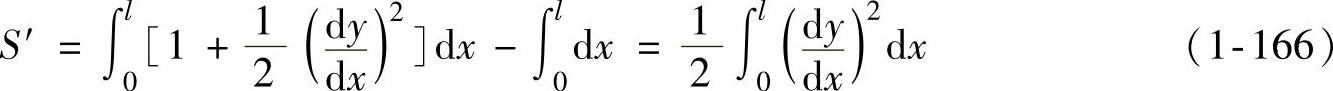
假定凸缘上的平均切向压应力为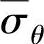，则半波上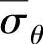因长度缩短而释放出的能量为

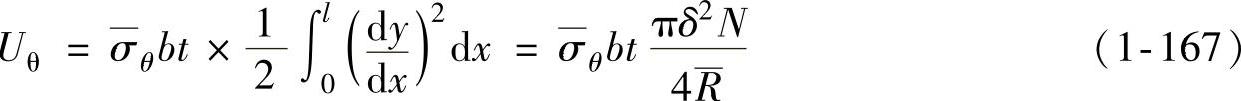
（3）U_Q不用压边力时，凸缘内边沿在凸模与凹模圆角之间加持得很紧，实际上也有阻止起皱的作用。计算U_Q时应考虑以上因素。

利用有关薄板弯曲的现有公式：宽度为b的环形板，内周边固支，在均布载荷q的作用下，其平均半径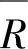处的挠度为

其中，C为与材料泊松比及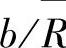

比值有关的系数，介于1.03～1.11之间。如果取平均值，则C＝1.07，则式（1-168）可以写作

其中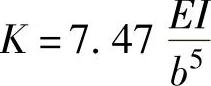，为常数，所以载荷q与挠度y成正比。

凸缘内边沿夹持得很紧，相当于周边固支的环形板，其阻止起皱的作用可以用上述均布载荷q的效应加以模拟，称为虚拟压边力。

起皱时，波纹隆起。虚拟压边力q所消耗的功U_Q为

将式（1-160）与式（1-168）代入式（1-170）可得

临界状态时，平均切向应力所释放出的能量恰好等于起皱所消耗的能量。根据式（1-153），将U_θ、U_w和U_Q值代入，可得

式（1-172）对波数微分，令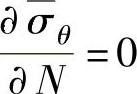，即可得临界状态下的波数N为

将N值代入式（1-172），即可求得凸缘起皱时的最小切向应力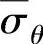为

不需压边的极限条件可以表示为

如果材料的一般性实际应力曲线为式（1-154），假定压延时，整个凸缘宽度上均为平均切向应力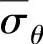作用。与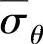相应的平均切向应变为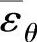，则

为简化计算，取

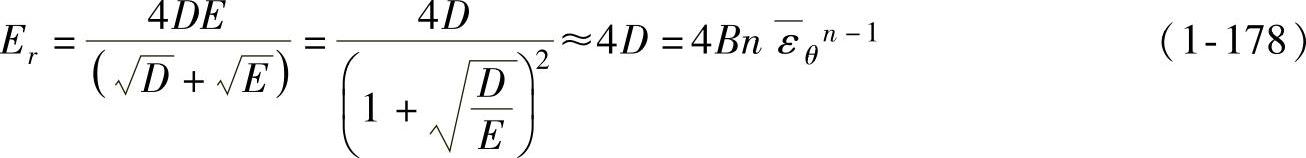
将式（1-178）代入式（1-174）可得

又因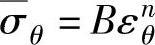，所以式（1-179）为

假定R₀为毛坯的半径，R_t为压延某一瞬时的凸缘外半径，r为凸缘内半径（即压延件半径），并以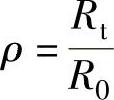表示压延时刻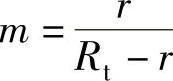，表示压延系数，式（1-180）中的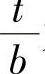为

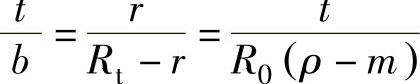
将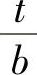的值代入式（1-180），则压延时不需压边的条件可表示为

假定凸缘上任意点R处的切应变与其位置半径成反比，即

凸缘外边沿的切应变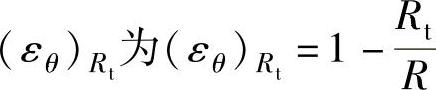

凸缘内边沿的切应变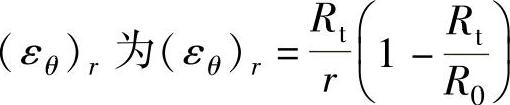

所以凸缘上的平均切应变为

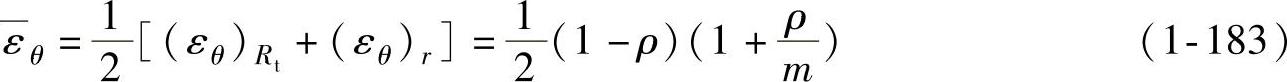
将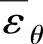值代入式（1-181），可得不需压边的条件为

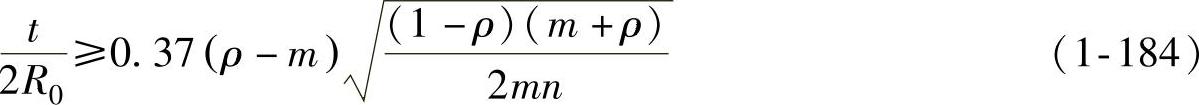
式（1-184）对ρ微分，令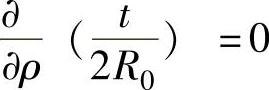，可得凸缘最易失稳的ρ值为

ρ＝0.675＋0.325m

将此值代入式（1-181），可得不需压边的条件为

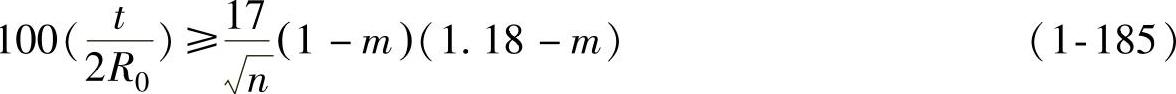
式（1-185）表明：压延时，材料的切线模量、压延系数和毛坯的相对厚度越大，不用压边的可能性也越大。

图1-20所示为按式（1-185）绘出的无压边压延起皱的临界曲线。此曲线与贝尔德文（P.Baldwin）的试验结果基本相符。

2.筒形件有压边压延时起皱的临界条件

首先，在试验研究的基础上，假定凸缘起皱后波纹表面的数学模型为（见图1-21）

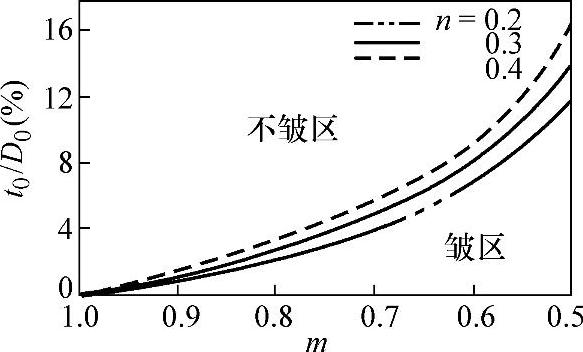
图1-20 无压边压延起皱的临界曲线

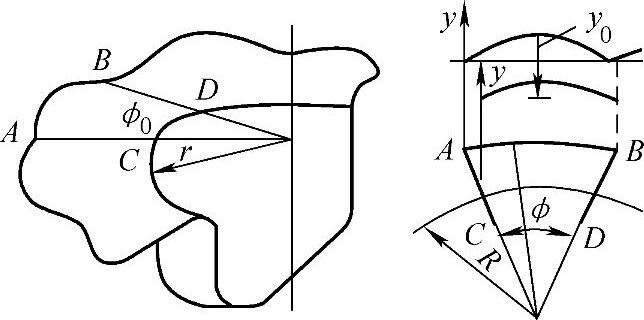
图1-21 凸缘起皱后波纹的几何图形

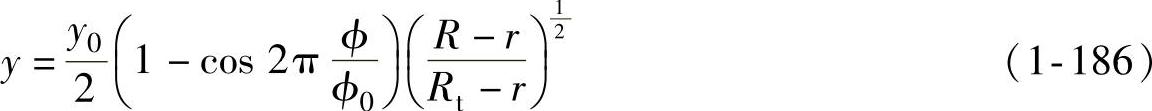
式中 R_t——某一压延瞬间凸缘的外半径；

r——凸缘的内半径（即筒形件的半径）；

R——凸缘上任意点的位置半径；

ϕ₀——单波所对的圆心角；

ϕ——单波中任意弧段所对的圆心角；

y₀——单波的最大挠度；

y——凸缘上任意点[坐标为（R，ϕ）]处的挠度。

显然，当R为任意值，但ϕ＝0或ϕ＝ϕ₀时，y＝0；只有当R＝R_t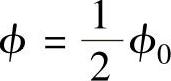，时，y＝y₀。

其次，确定每一压延阶段凸缘上的应力分布。

假设材料的实际应力曲线为式（1-154），为了简化计算，用式（1-179）计算任一点R处的切应变ε_θ，因为ε_θ为最大主应变，所以可以近似认为

将式（1-184）与平衡方程、塑性方程联立求解可得

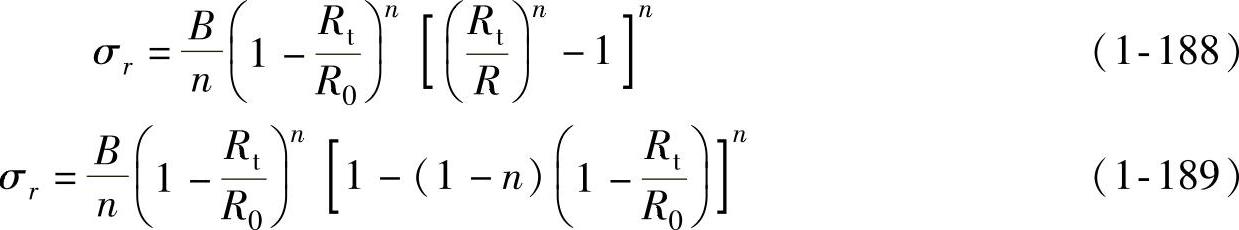
最后，由于采用了压边，波纹挠度不大，可以认为失稳是在加载条件下发生的。分析计算中可用切线模量D代替弹性模量E，有

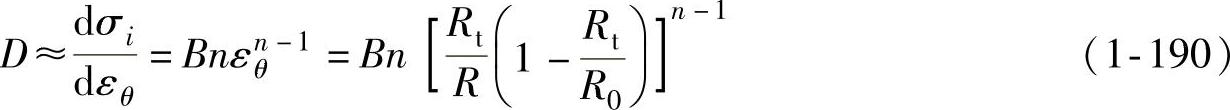
用能量法，将U_θ、U_w、U_Q各项按单波逐一计算如下：

（1）U_θ（见图1-22）假定任意R处的切应力为σ_θ，σθ的作用面积为tdR（t为板厚），将式（1-186）及x＝Rϕ的关系代入式（1-154）可得R处单波的缩短量S为

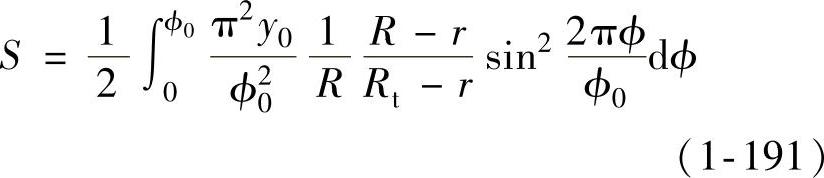
在一个单波内，切应力σ_θ由于长度缩短而释放出的功为(www.xing528.com)

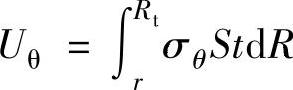
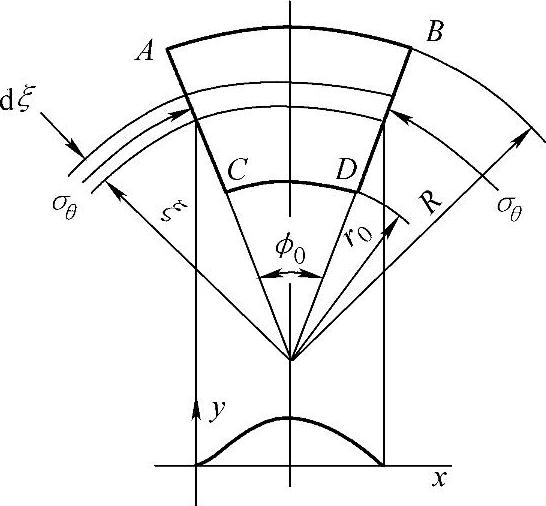
图1-22 筒形件有压边压延时凸缘起皱后单波纹的受力分析

将式（1-186）和式（1-188）代入上式可得

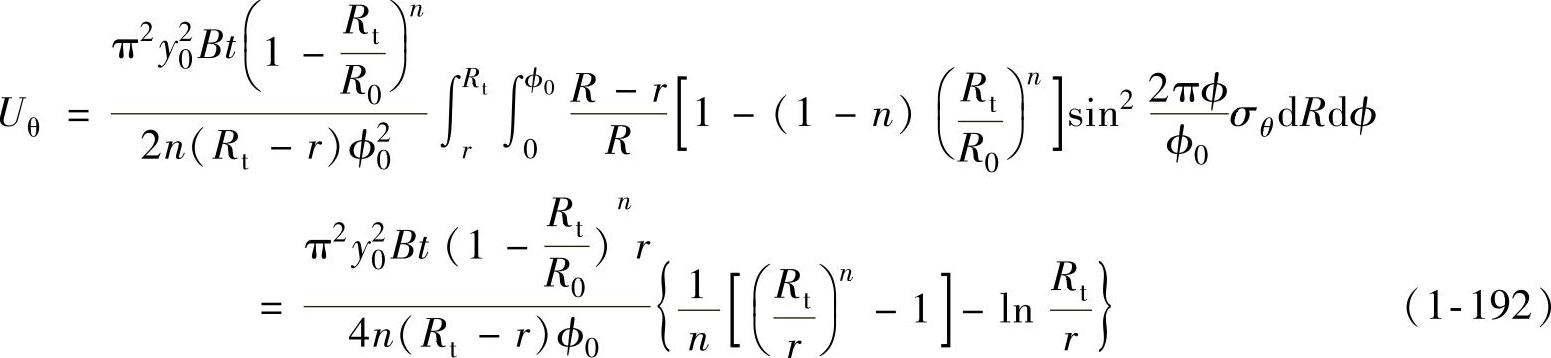
（2）U_w利用式（1-161），并以D代替E，可得失稳时单波所需的弯曲能为

式中 dI——在半径R处，厚为t、宽为dR剖面的惯性矩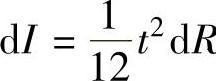：。将此关系与式

（1-186）、式（1-190）代入式（1-193）可得

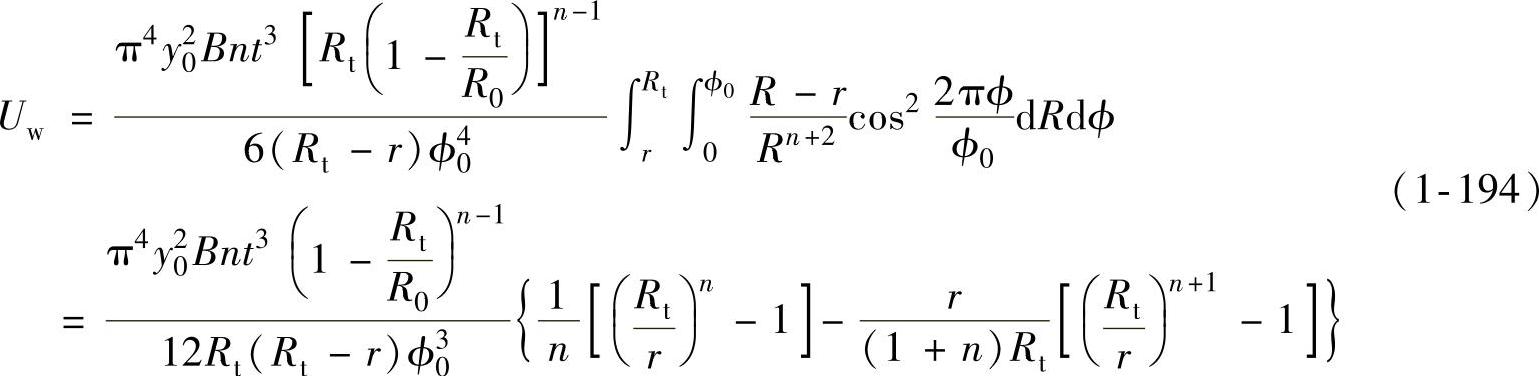
（3）U_Q忽略虚拟压边力的作用。假定总压边力为F_Q，总波数为N，压边力基本上作用在凸缘边沿R＝R_t处，此处挠度最大，等于y₀，因此每一波纹上所消耗的压边功U_Q为

将式（1-192）～式（1-194）代入式（1-153），可以解得压边力F_Q为

将式（1-196）对ϕ₀微分，令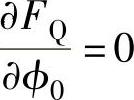，即可求得最小压边力下的ϕ₀为

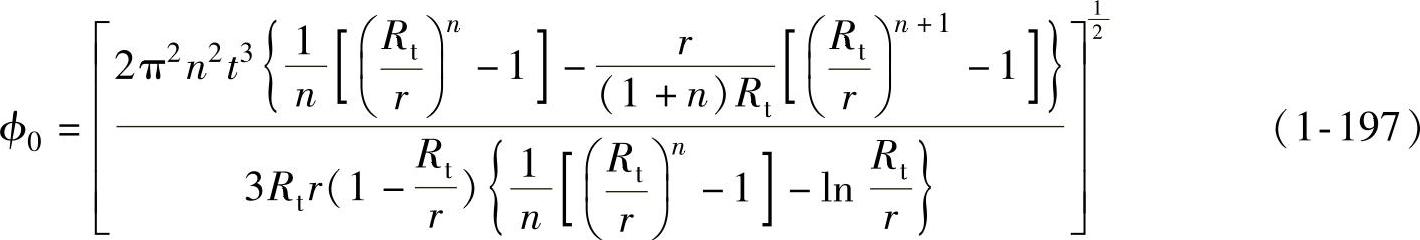
将ϕ₀值代入式（1-196），即可求得最小压边力F_Q为

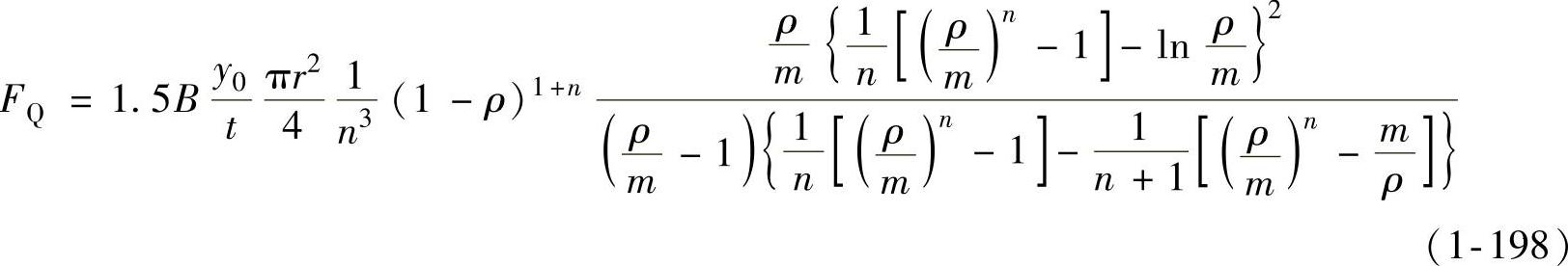
其中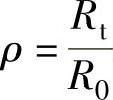，表示压延时刻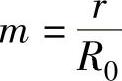，为压延系数。由式（1-198）可知：在不同的压延阶段，压边力也不同。其值与板料性质（B、n）、压延系数（m）、压边后的波纹最大相对高度（y₀/t）（一般取为0.13左右）、1/4筒形件面积（πr²/4）等因素有关。

在式（1-198）中，取

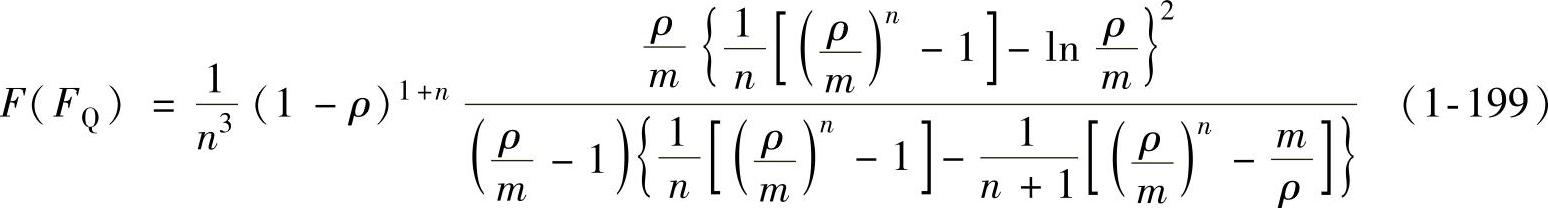
于是压边力F_Q为

F（F_Q）称为压边力系数，它是随压延系数、材料的切线模量、压延时刻而变化的函数。图1-23所示即为F（F_Q）的变化规律。F（F_Q）的变化规律与压边力F_Q的变化规律基本一致。

试验结果证明，式（1-198）是成立的，以此设计压延机床或调节压边力，可以大大改进压延过程。

3.考虑摩擦的法兰起皱临界条件

燕山大学的赵军教授在研究平底圆锥形件的过程中，在前人研究的基础上发展了法兰起皱的临界压边力的解析解。其基本原理是相同的，不同之处就是考虑了摩擦的影响，使得结果更接近实际情况，具体过程如下。

假定法兰起皱后波纹表面的数学模型为（见图1-24）

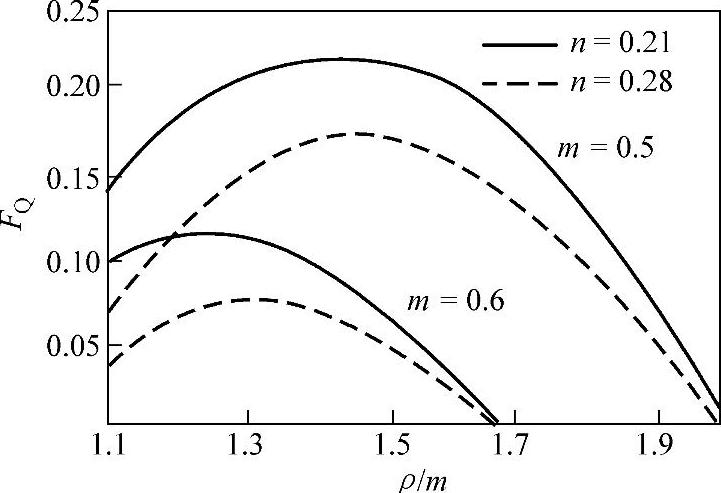
图1-23 压延过程中压边力的变化规律

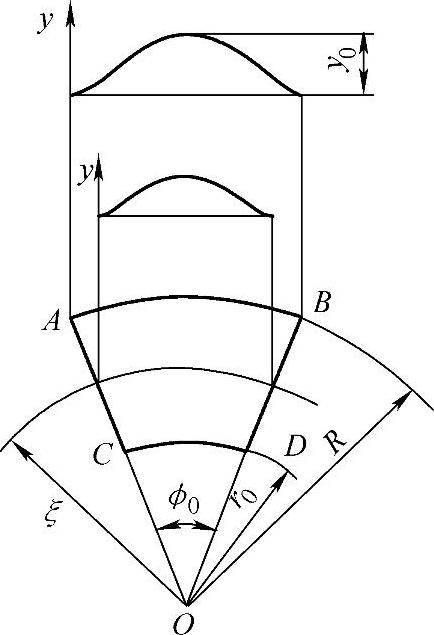
图1-24 法兰起皱后波纹表面的数学模型

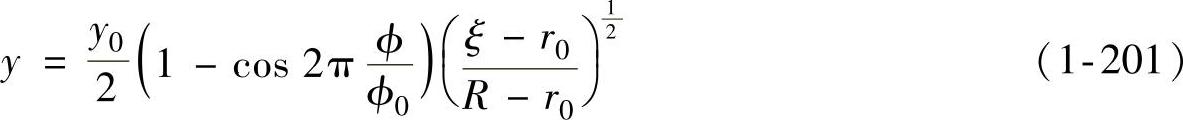
式中 R——拉深任意时刻的法兰外半径；

r₀——法兰内半径；

ξ——法兰上任一质点的径向坐标；

ϕ₀——单波所对应的圆心角；

ϕ——单波任一弧段所对应的圆心角；

y₀——单波的最大挠度；

y——法兰上任一质点[坐标为（ξ，ϕ）]处的挠度。

显然，当ξ为任意值，但ϕ＝0或ϕ＝ϕ₀时，y＝0；只有当ξ＝R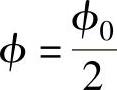，时，y＝y₀，此时波纹的挠度最大。

在以下分析中要用到波纹挠度的一阶导数和二阶导数，在此一并给出，即

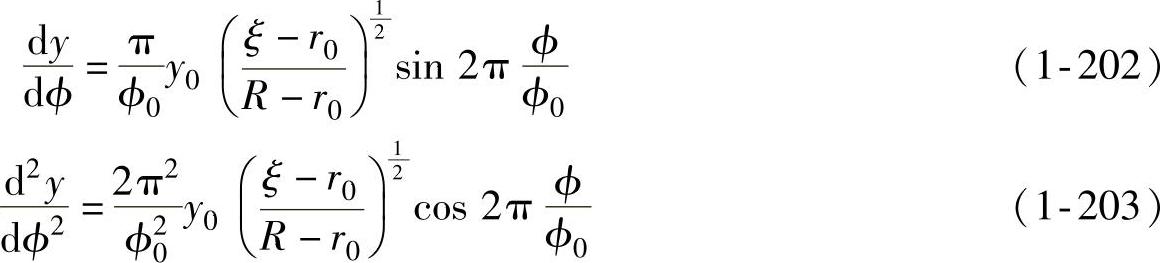
数值分析和试验研究结果都表明，无论是筒形件还是锥形件，拉深过程中法兰变形区等效应变从法兰外缘到法兰内缘是逐渐增大的，即等效应变值与径向位置坐标成反比。鉴于此，为了简化计算，使能量法求解的后续处理能够得以继续，设等效应变与瞬时径向坐标成简单的反比例关系，即

法兰外边缘可近似为单向压缩应力状态，其等效应变等于周向应变的绝对值，即ε_1ξ＝R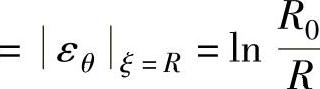，所以

假设硬化规律服从式（1-154），则等效应力分布应为

应用法兰变形区瞬时应力平衡方程和Tresca屈服准则可得

将作用在法兰外边缘的压边力F_Q所引起的附加径向拉应力作为应力边界条件处理，则有

这样可得应力分布近似解为

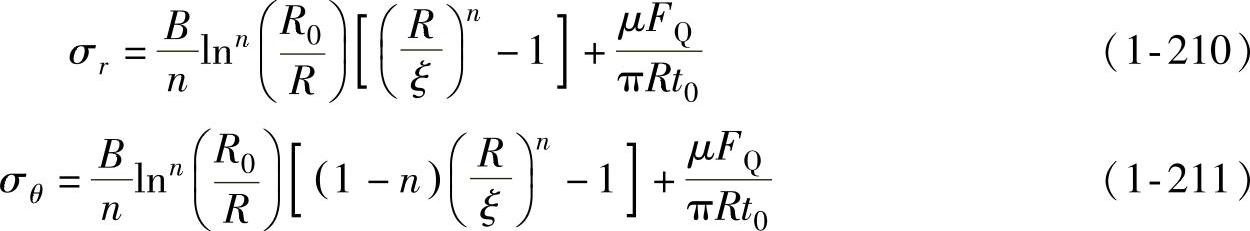
上述应力分布近似分析中忽略了法兰变形区板厚变化的影响，但考虑了压边力F_Q所引起的径向附加拉应力的影响。这样便将润滑条件（即摩擦系数μ）引入了法兰起皱临界压边力的分析中，可以得到润滑条件对法兰起皱临界压边力影响的定量分析结果。

将式（1-153）中各项能量按单波逐一计算如下。

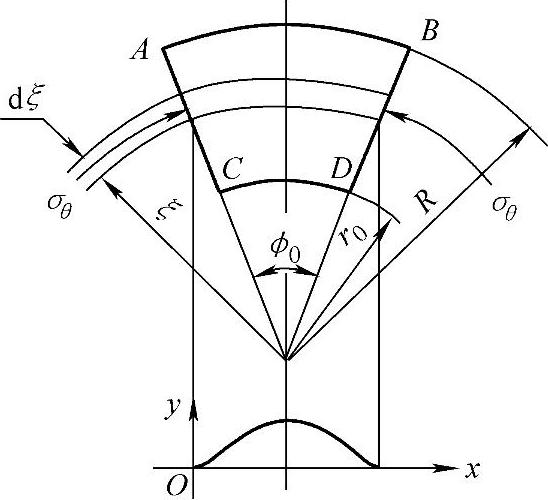
如图1-25所示为法兰起皱后单波纹的受力分析。假定任意ξ处的周向应力为σ_θ，σ_θ的作用面积为t₀dξ（t₀为板厚）。失稳起皱后周长缩短，单波的周长缩短量为

式中 dS、dx——单波微分段的弧长及其在x轴上的投影长度。

又因为

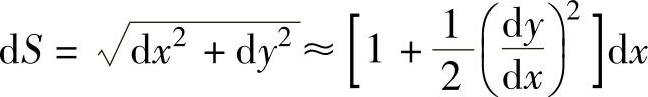
图1-25 法兰起皱后单波纹的受力分析

所以

因为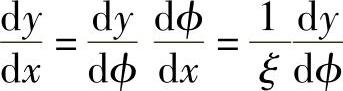，则可得

在一个单波内，周向应力σ_θ由于长度缩短而释放出的功为

其中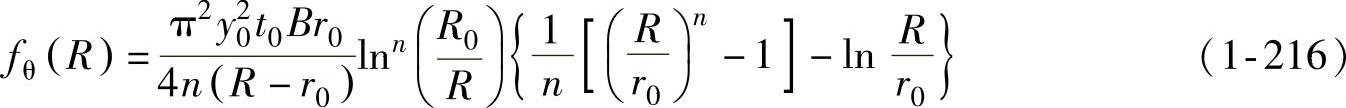

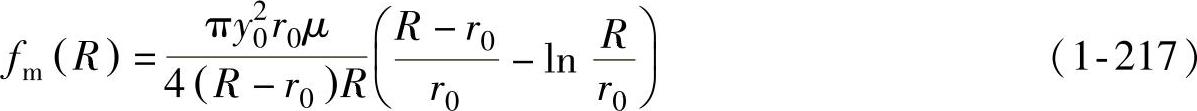
材料力学中有关梁的弹性弯曲能量公式为

式中 E——材料的弹性模量；

I——梁的截面惯性矩；

l——梁的长度；

y（x）——梁的挠度曲线。

法兰起皱波纹隆起时是塑性弯曲，不是弹性弯曲。但由于采用了压边圈，波纹挠度不大，可以认为失稳是在加载条件下发生的，并仍然满足弹性弯曲时有关变形的假设，分析计算中可用切线模量D代替式（1-218）中的弹性模量E。波纹挠度与坐标ξ有关，求解弯曲能时还需对ξ进行积分，因此，失稳时单波所需的弯曲能应为

其中，dI为半径ξ处，厚度为t₀、宽度为dξ剖面的惯性矩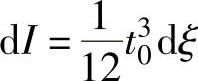，。因为x＝ξϕ，dx＝ξdϕ，并且

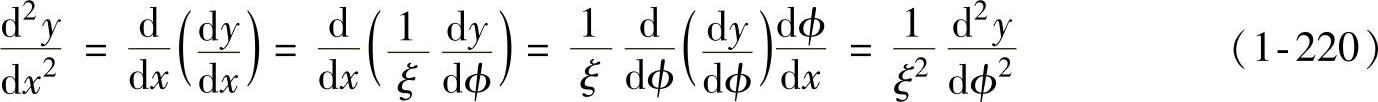
将式（1-220）及式（1-201）和式（1-155）代入式（1-217），积分后化简可得

其中

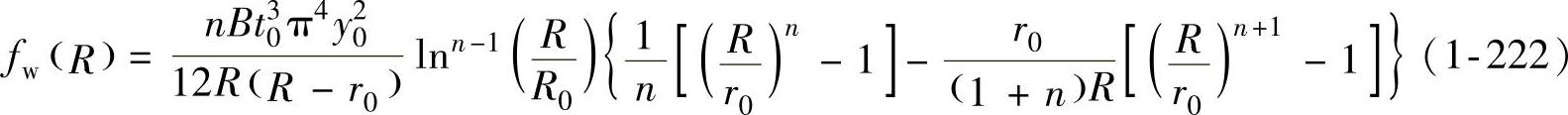
假定总压边力为F_Q，总波数为N，则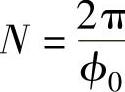，压边力基本上作用在法兰外边缘ξ＝R处，此处挠度最大，其值为y₀，因此每个波纹上所消耗的压边功为

将式（1-214）、式（1-218）及式（1-223）代入式（1-153），可解得压边力F_Q为

将式（1-222）对ϕ₀进行微分，令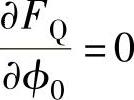，即可求得最小压边力下的ϕ₀为

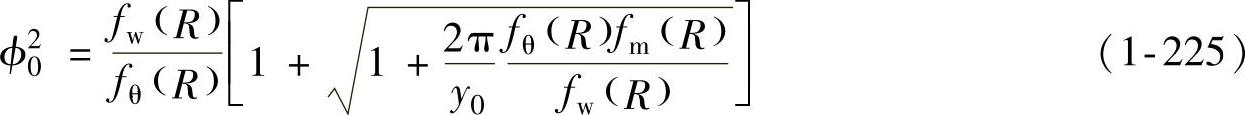
将该值代回式（1-222）即可求得法兰起皱的临界压边力理论计算公式为

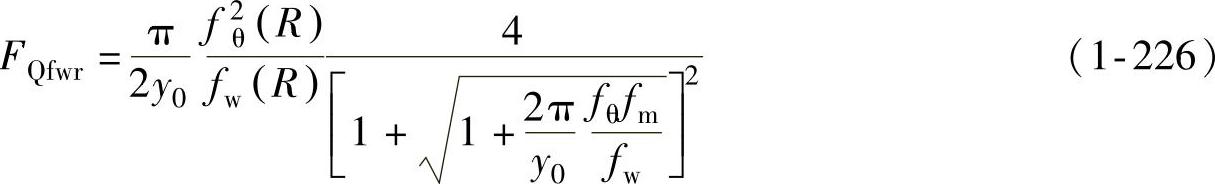
式（1-224）中最后一个分式是润滑条件对临界压边力值的影响因子。当μ＝0时，f_m（R）＝0，该分式值为1；当μ﹥0时，f_m（R）﹥0，该分式值小于1。所以，考虑摩擦影响时的临界压边力曲线比不考虑摩擦时要低，摩擦系数越大，所需的防皱压边力越小。

为了能够更清楚地了解影响法兰起皱临界压边力的各种因素，将式（1-216）、式（1-217）和式（1-222）代入式（1-224），化简后进行整理。为此令

其中，ρ表示拉深时刻，m是拉深系数，则有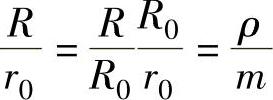。再重新定义几个无量纲因子，则法兰起皱临界压边力可表示为

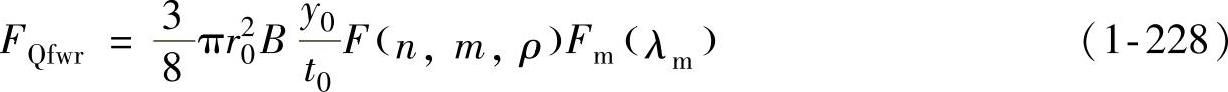
其中，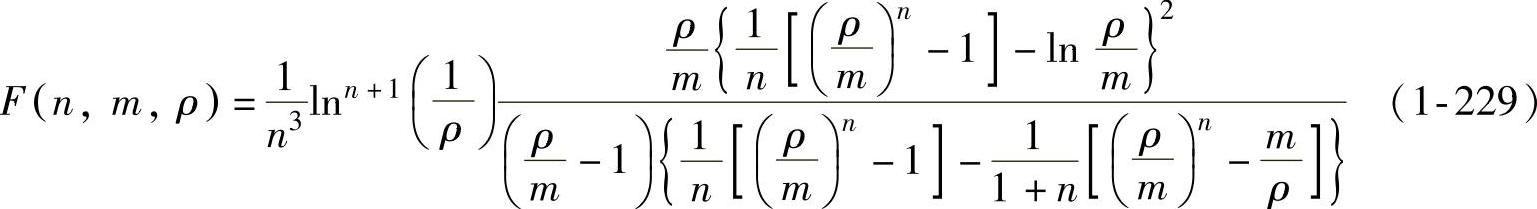

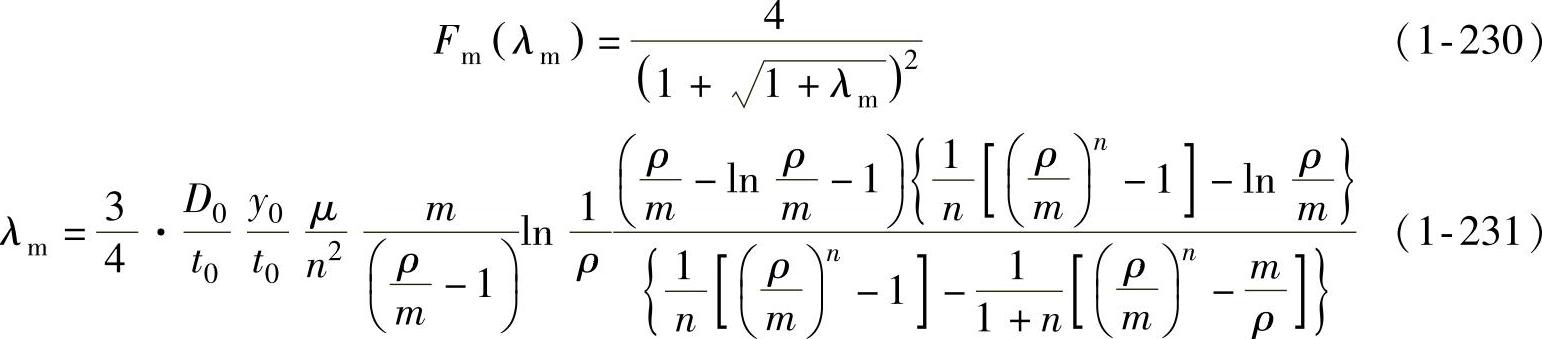
由式（1-228）～式（1-231）可知：在不同的拉深阶段，法兰起皱的临界压边力也不同，其值与板材性质（B、n）、拉深系数m、压边后的波纹最大相对高度y₀/t₀（一般取为0.13左右）、凹模口面积πr²₀、摩擦系数μ以及毛坯相对厚度t₀/D₀等因素有关。

图1-26所示为三种板材锥形件拉深时法兰起皱临界压边力F_Qfwr变化规律的理论计算曲线。钢板的拉深系数为m＝0.615，铝合金板的拉深系数为m＝0.64。临界压边力在拉深过程的中后期出现极大值F^max_Qfwr，采用恒力压边时，F^max_Qfwr即为恒定压边力选择范围的下限值。

图1-27所示为板材的硬化指数n及拉深系数m变化时对法兰起皱临界压边力的影响。图中的纵坐标是临界压边力无量纲因子，它与临界压边力F_Qfwr的变化规律相同。拉深系数m对临界压边力F_Qfwr的影响极为显著。拉深系数越小，法兰区的变形程度越大，所需的防皱压边力也越大。其他条件相同时，材料的硬化指数n越大，所需的防皱压边力则越小，这说明材料的应变硬化效应对法兰起皱有明显的抑制作用。此外，n值较大时，临界压边力的极大值向拉深过程的后期偏移。这种现象有利于变压边力拉深时提高拉深极限。

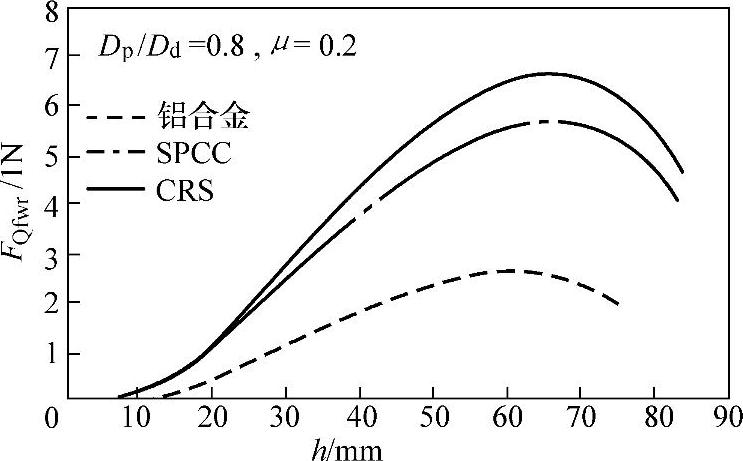
图1-26 法兰起皱临界压边力变化规律的理论计算曲线

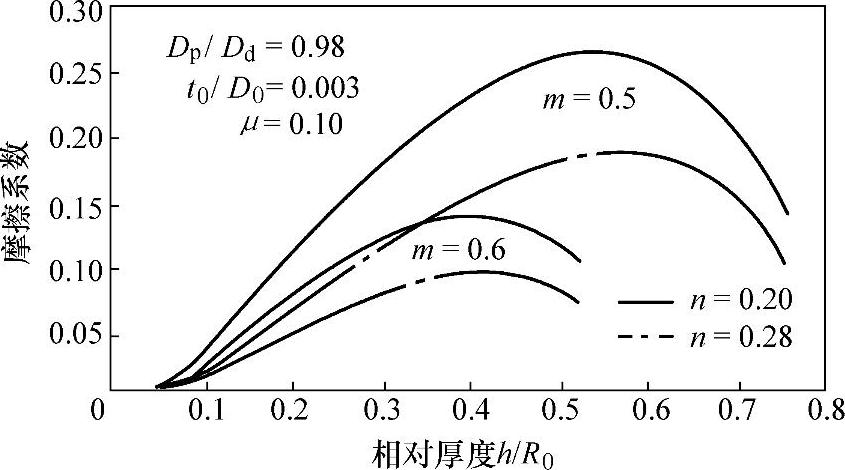
图1-27 拉深系数和硬化指数对法兰起皱临界压边力的影响

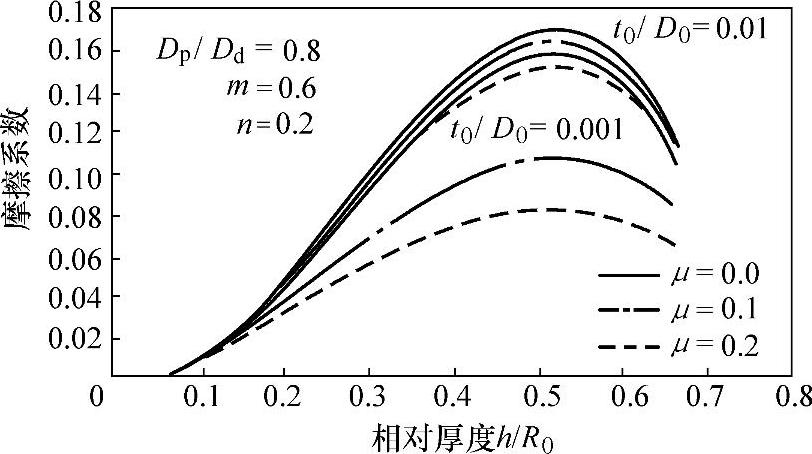
图1-28 摩擦系数和毛坯相对厚度对法兰起皱临界压边力的影响

图1-28所示为摩擦系数μ和毛坯相对厚度t₀/D₀对法兰起皱临界压边力变化的影响。毛坯相对厚度t₀/D₀较大时，摩擦系数μ对临界压边力F_Qfwr的影响不大，但当毛坯相对厚度t₀/D₀较小时，摩擦系数μ对临界压边力F_Qfwr的影响却非常显著。当毛坯相当厚度较小而摩擦系数较大时，最大临界压边力F^max_Qfwr可以减小1/3～1/4。

以往对法兰起皱临界压边条件的认识没有考虑润滑条件的影响，无论是理论分析公式还是经验公式，也均未涉及摩擦系数μ。在大型汽车覆盖件拉深成形时，毛坯相对厚度值都很小，且在很多情况下按经验公式确定的压边力值远大于拉深力值。因此，要求拉深设备的压边滑块（外滑块）应具有不低于成形滑块（内滑块）的吨位。通过以上分析可知，当毛坯相对厚度较小时，可以通过改变润滑条件的方式大大降低防皱压边力，这对大型汽车覆盖件的拉深成形具有重要意义。即采取适当改变润滑条件的措施可大大降低对成形设备压边吨位的要求。进而把润滑条件作为工艺参数来调节，可达到改善拉深工艺的目的（应增大摩擦系数，而不是减小摩擦系数），这也开拓了一种新的工艺调节方法。