用能量法解析1.9.3拉深力-行程曲线

1.基本假设

（1）直母线假设 试验表明，在锥形件的拉深过程中，其3区悬空部分径向剖面的轮廓线是一未知曲线。该曲线的曲率变化与材料的性能参数、坯料的相对厚度、润滑条件、压边力大小及模具几何参数等因素有关，但其曲率变化并不大。为便于进行解析分析，可将该曲线近似为一直线，即认为变形过程中任一时刻3区悬空侧壁部分的母线均为一直线，并在B、C处与凸、凹模圆角相切，如图1-17所示。

根据直母线假设和图1-17所示的几何关系可知，即

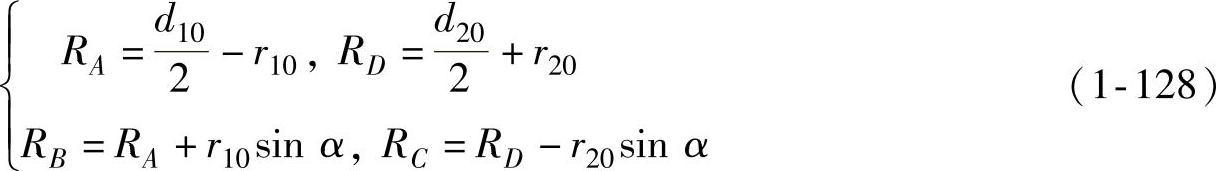
令

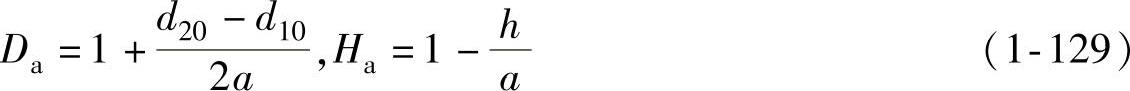
则由图1-17可得拉深高度h与α之间的关系为

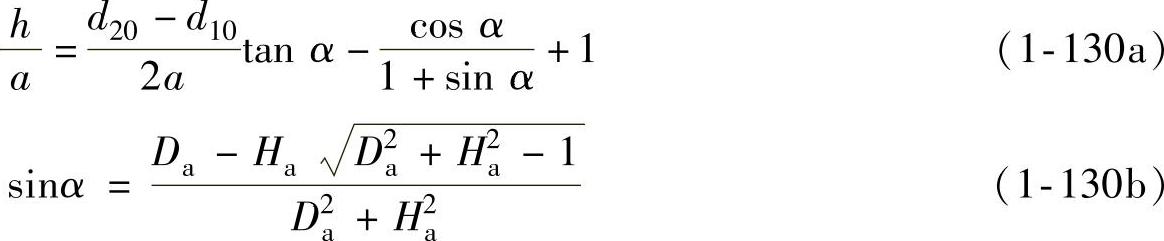
（2）面积不变假设 轴对称曲面件拉深过程中毛坯厚度的变化是不均匀的，凸模底部及凸模圆角部分略有变薄，凹模圆角和法兰部分略有增厚。为便于分析，设其平均厚度与变形前相同，则塑性变形的体积不变条件转化为面积不变。

根据面积不变假设，拉深过程中法兰外边缘的半径R可通过变形前后毛坯的总面积不变直接给出，即

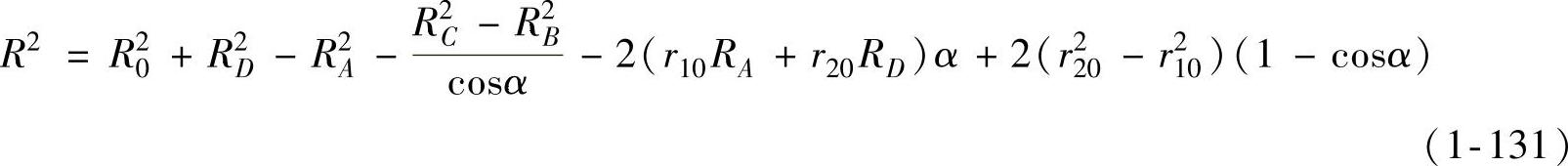
各变形区内质点的瞬时径向坐标ξ与凸模行程h及原始径向坐标ρ之间的关系ξ＝ξ（ρ，h），可由变形前后质点所在位置以内（或以外）的面积不变直接给出，即

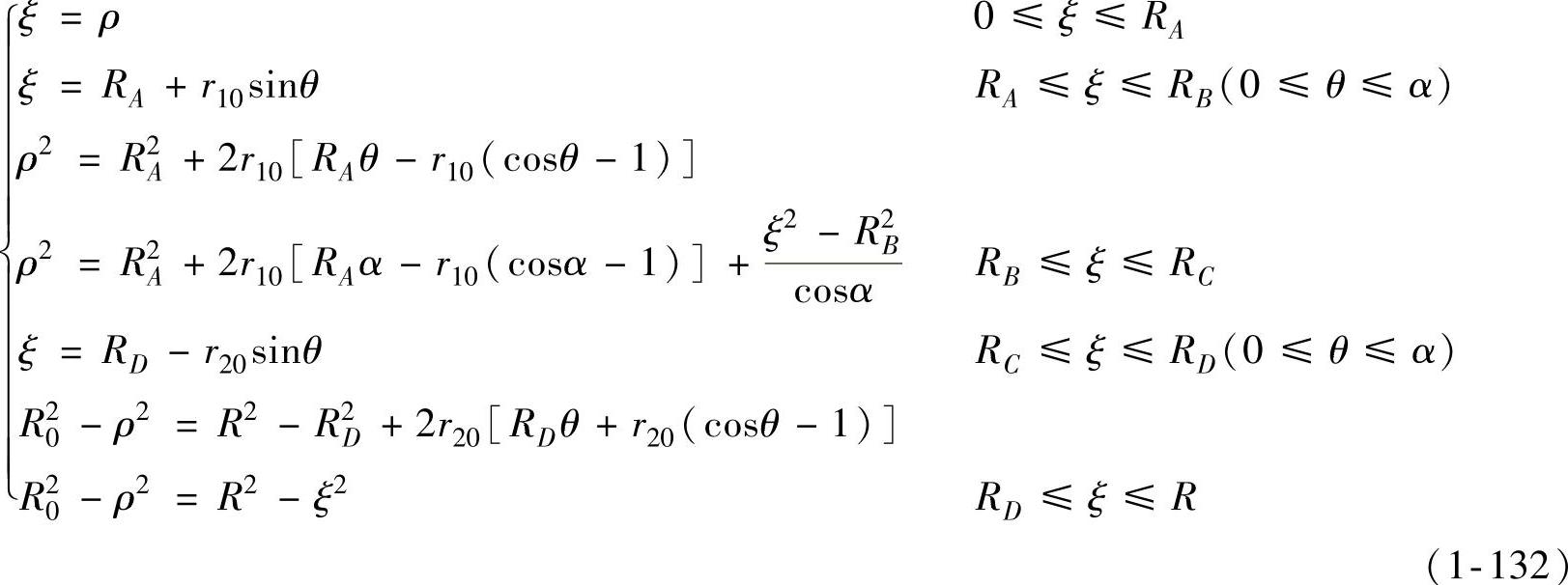
（3）似直梁弯曲假设 如图1-15所示，轴对称曲面件拉深时在B、C和D处曲率有突变，即存在塑性弯曲变形，但属于三维壳体塑性变形中的复杂塑性弯曲，目前尚无简便且合适的处理方法。此处参照直梁的塑性弯曲理论，假设弯曲面上的弯矩由中性层以内使金属产生塑性流动的-σ和中性层以外使金属产生塑性流动的＋σ构成。因此，周向单位弧长上的弯矩应为t²₀σ/4，整个弯曲面上的弯矩为

式中 σ——弯曲面上的等效应力；

i——弯曲面所在的位置。

2.基本方程

（1）薄板成形轴对称几何方程 对于轴对称薄板成形问题，当变形前为平板毛坯，变形后成为轴对称空间壳体时，板面内的两个主应变取决于变形后壳体的轮廓形状及质点的瞬时径向坐标与原始径向坐标之间的关系，即其几何方程可表达为

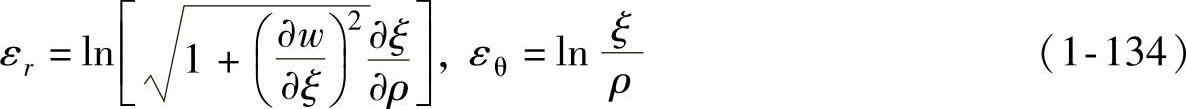
（2）塑性流动方程 忽略弹性变形，考虑板材面内同性、厚向异性特点，符合R.Hill的塑性流动方程，即

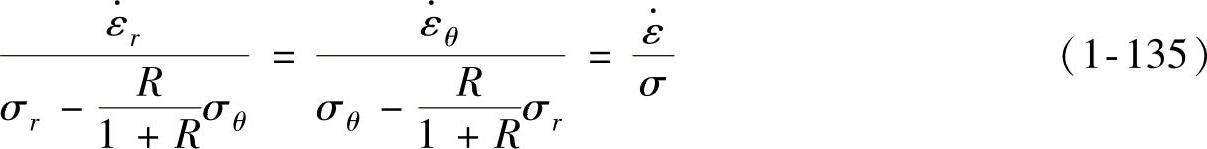
式中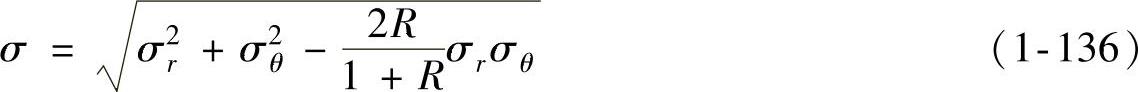

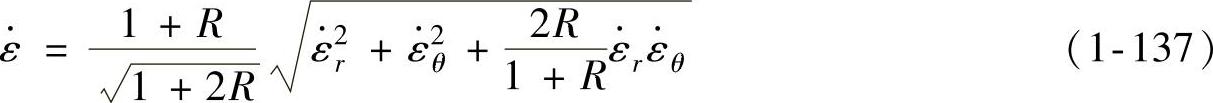
类似地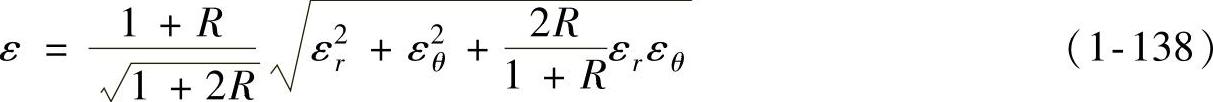

式中 R——板材的厚向异性系数；

σ、ε和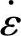——质点的等效应力、等效应变和等效应变速率。

（3）塑性本构方程 设板材变形过程中等效应力与等效应变之间的关系与单向拉伸时的真实应力和真实应变之间的关系相同，符合指数硬化规律，即

σ＝Bεⁿ （1-139）

式中 B——板材的强度系数；

n——硬化指数。

（4）基本能量方程 设刚塑性变形体的体积为V，总表面积为S，受表面力T_i作用而处于塑性状态，其应力场为σ_ij，位移速度场为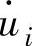，应变速率场为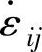，则其基本能量方程为

对于图1-17所示的轴对称曲面件拉深成形，式（1-140）的左端应包括外载荷单位时间内所做的功及4区和5区接触面摩擦力单位时间内所消耗的功；式（1-140）的右端应包括3、4、5区单位时间内的塑性变形功以及B、C、D处单位时间内的弯曲变形功。(www.xing528.com)

3.各变形区质点的等效应变

将面积不变假设及轴对称几何方程（1-134）代入等效应变表达式（1-138）可知

其中

再将式（1-132）代入式（1-141）可得各变形区的等效应变为

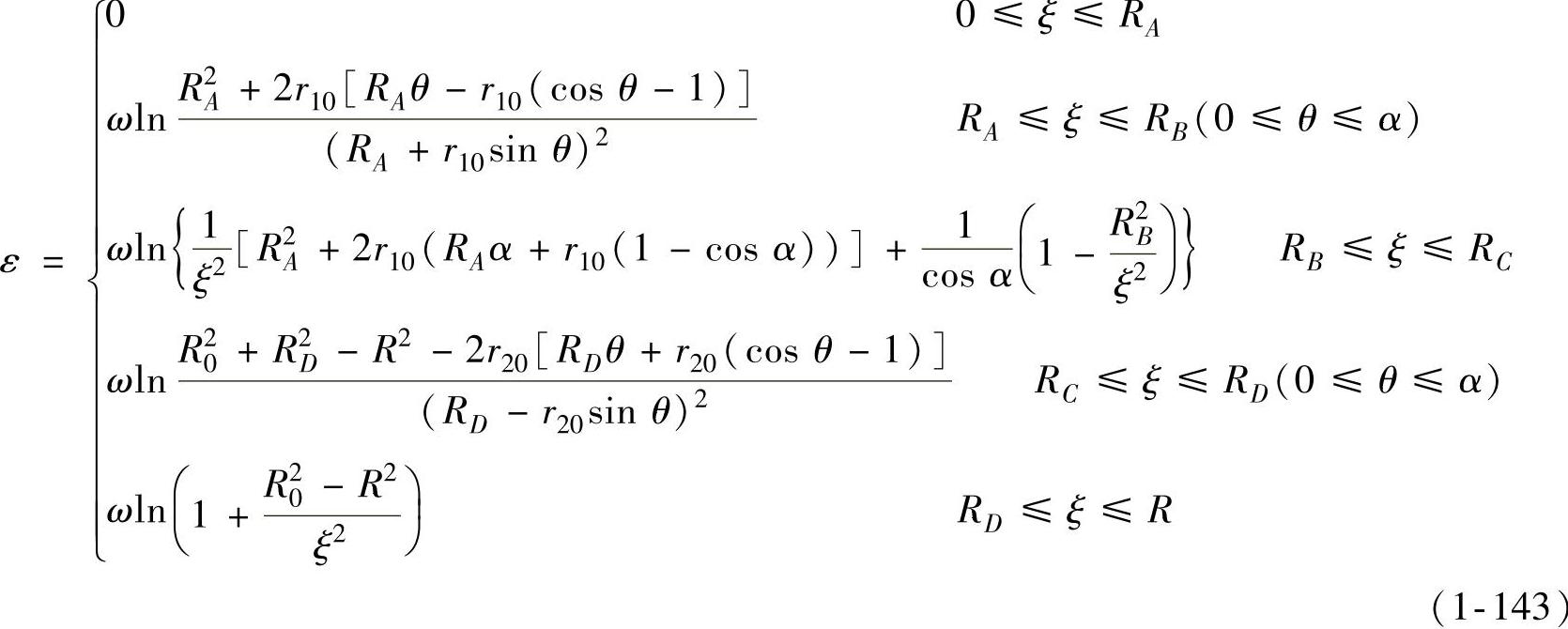
4.各变形区质点的流动速度和等效应变速率

设冲头的位移速度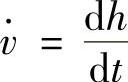，则根据式（1-123）可知各变形区质点的径向位移速度为

由式（1-130a）和式（1-131）可得到两个推导过程中非常有用的中间导数关系，即

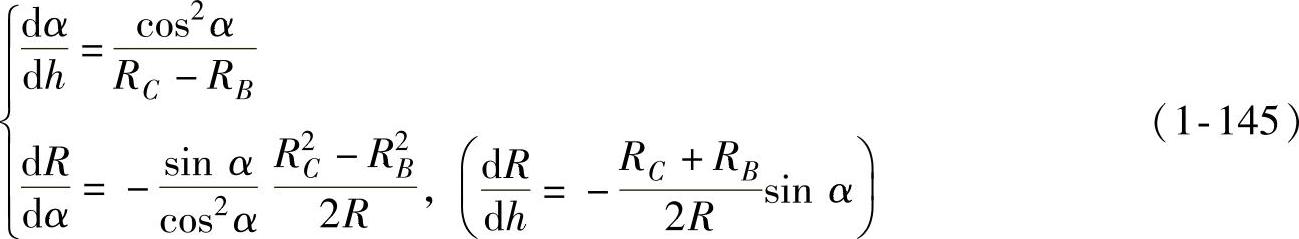
将式（1-132）代入式（1-144）并用式（1-145）化简，便可得到各变形区质点的径向位移速度为

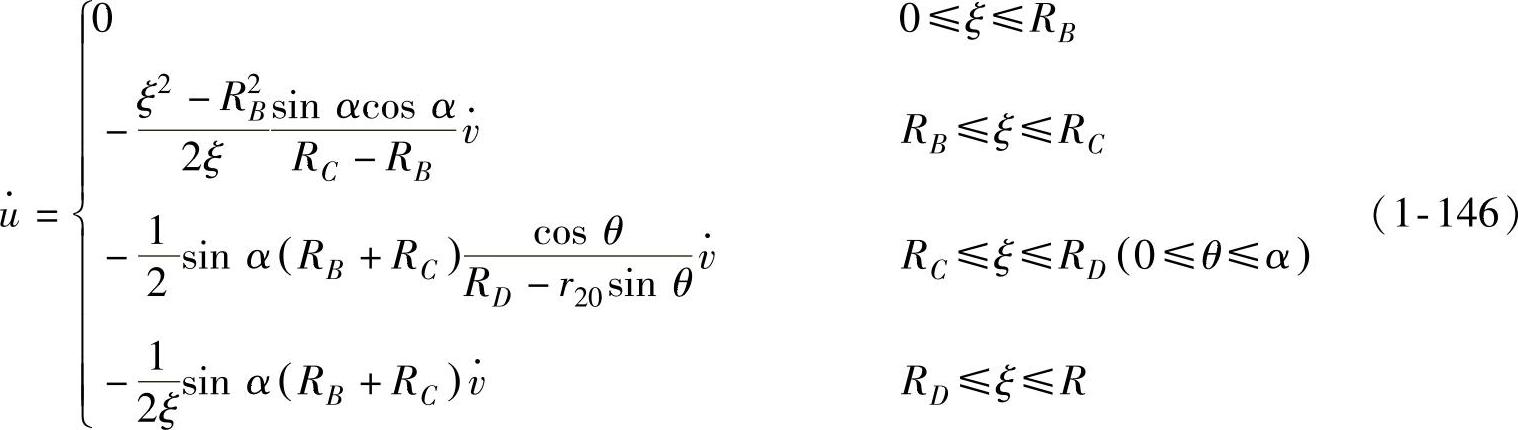
如图1-18所示，4区和5区的摩擦应力作用方向与质点的绝对流动速度方向相反，但都是沿着质点所在位置成形件轮廓线的切线方向。设质点绝对流动速度方向与径向位移速度之间的夹角为θ，则摩擦面上的质点绝对流动速度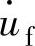应为

在第4变形区，0≤θ≤α；在第5变形区，θ＝0。

因为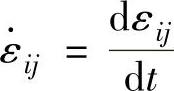，应用面积不变假设及式（1-134）和式（1-138）则有

将式（1-146）代入式（1-148）可得各变形区质点的等效应变速率为

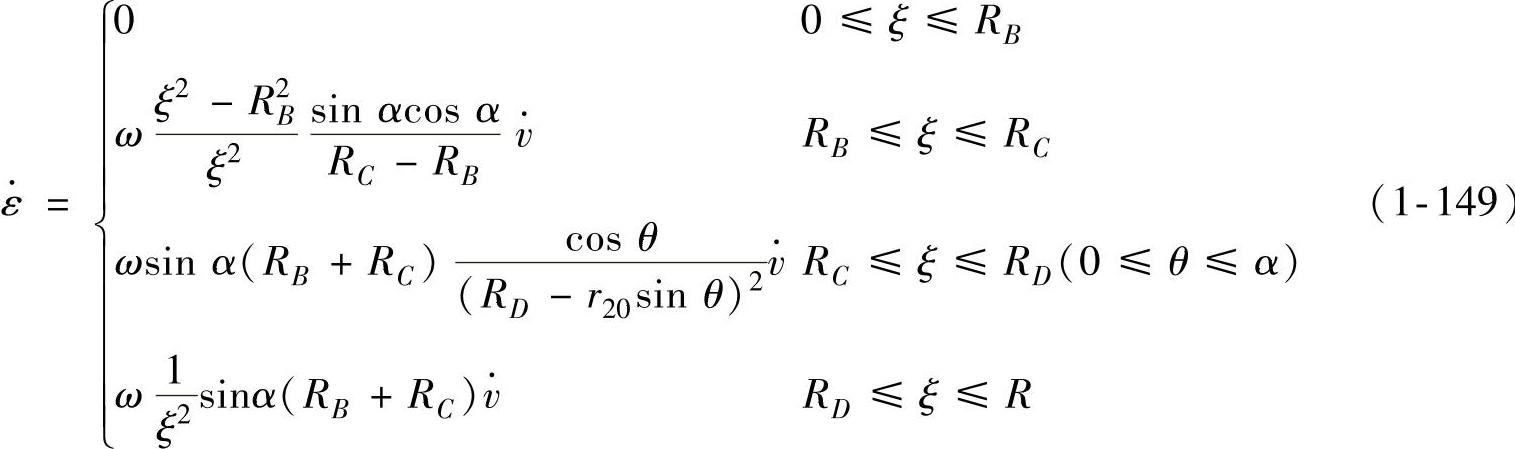
5.拉深力-行程曲线的解析公式

利用塑性流动方程式（1-135）～式（1-137）不难证明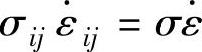。将此结论及式（1-147）、式（1-148）代入基本能量方程式（1-140），可得轴对称曲面件拉深力的一般表达式为

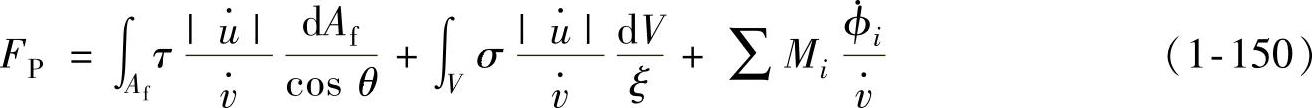
式中

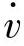——冲头的位移速度；

A_f——摩擦接触面的面积；

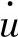——质点径向位移速度；

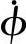——弯曲面的弯曲角速度，具体表达方式见式（1-151）。

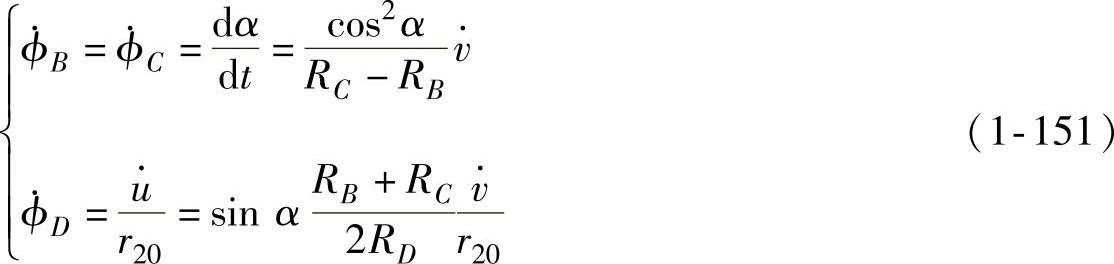
将摩擦应力分布式（1-124）～式（1-127）、质点径向位移速度分布式（1-146）及弯曲面弯矩式（1-133）、弯曲面弯曲角速度式（1-151）代入式（1-150）化简整理，可得到拉深力-行程曲线的解析公式为

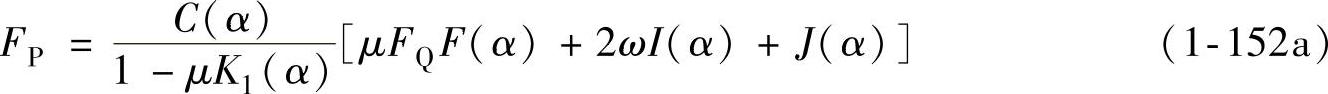
其中