力学解析：1.8.4薄板自由胀形

1.几何的约束方程

因为H＝H（t），ξ＝ξ（r，H），所以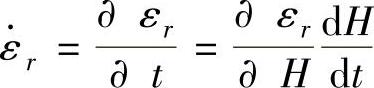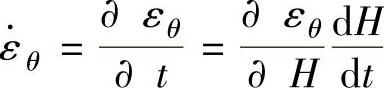，。由式（1-87）、式（1-96）和式（1-97）可得

其中

自由胀形时应变速率与应变主轴重合，故可对式（1-99）积分，根据自由胀形的初值条件，即

ε_r1H＝0＝ε_θ1H＝0＝0 （1-101）

则有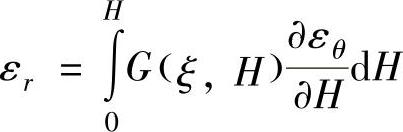

即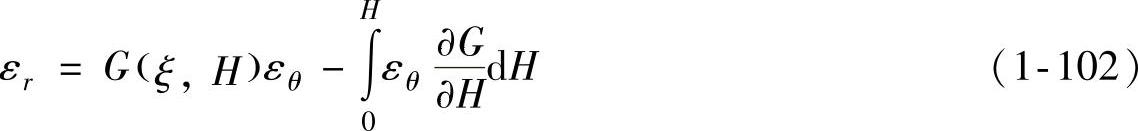

将式（1-79）和式（1-80）代入式（1-102），经整理后可得到

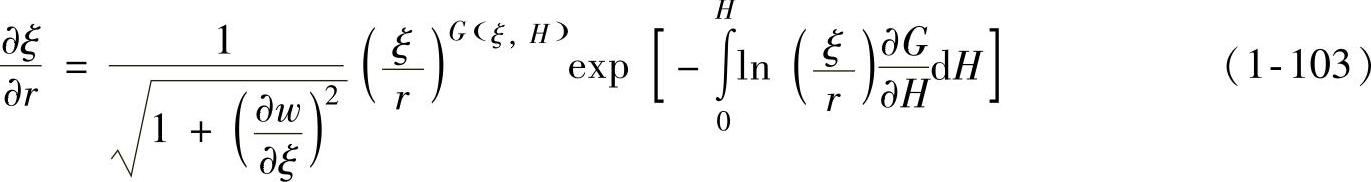
至此，问题归结为求解方程（1-103），其边值条件为

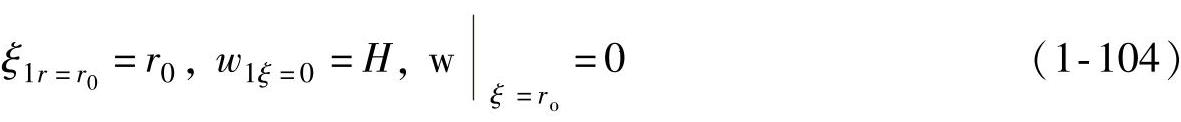
引入球壳假设后，胀形过程中轮廓方程便是已知的了，由图1-16所示的球面胀形假设示意的几何关系可知

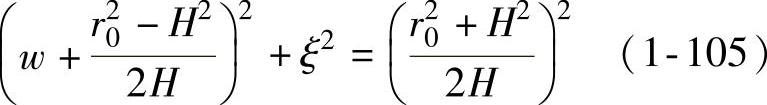
2.球壳假设条件下的解析解

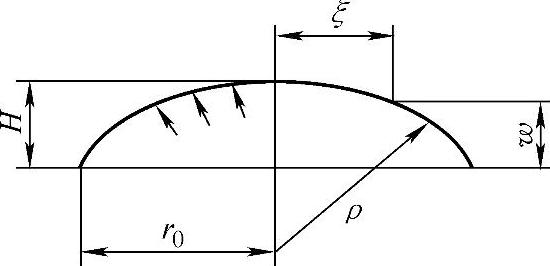
图1-16 球面胀形假设

均匀球壳假设包括两层含义：①胀形过程中板厚s只随胀形高度H变化，不随几何坐标变化；②胀形轮廓是球壳的一部分。

由宏观体积不变条件（πr₀²s₀＝2πρHs）及图1-16所示的几何关系[ρ²＝（ρ-H）2＋r₀²]可得

由于引入了球壳假设，则有ρ_r＝ρ_θ＝ρ，即N＝1，代入式（1-95）可得σ_θ＝σ_r，所以由式（1-96）可知F＝1，再由式（1-100）可得G＝1。代入式（1-99）和式（1-102）又可得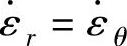，εr＝εθ。至此，由式（1-98）可求得应力场，由式（1-81）和体积不变条件ε_r＋ε_θ＋ε_s＝0可求得应变场。为简化表达式，令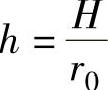，则有

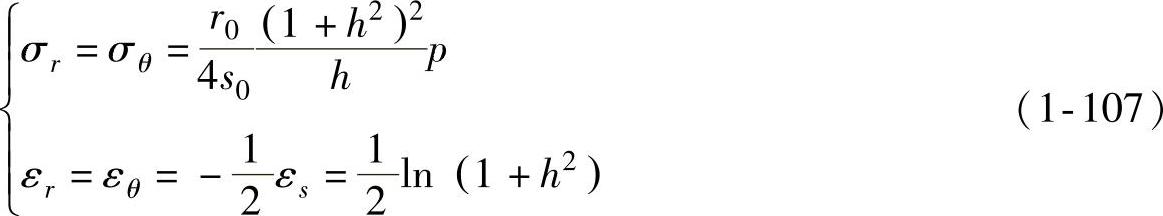
应变分量对时间求导可得应变速率场

再将式（1-107）和式（1-108）代入式（1-88）～式（1-90）可得

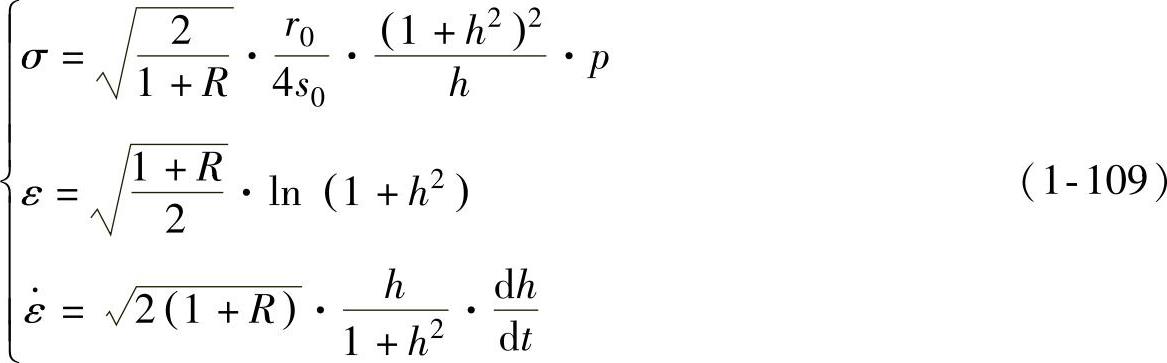
（1）常规塑性材料的解 对于常规塑性材料，将式（1-109）代入式（1-92）可得到胀形压力p与胀形高度H之间的关系，再代回式（1-107）则有(www.xing528.com)

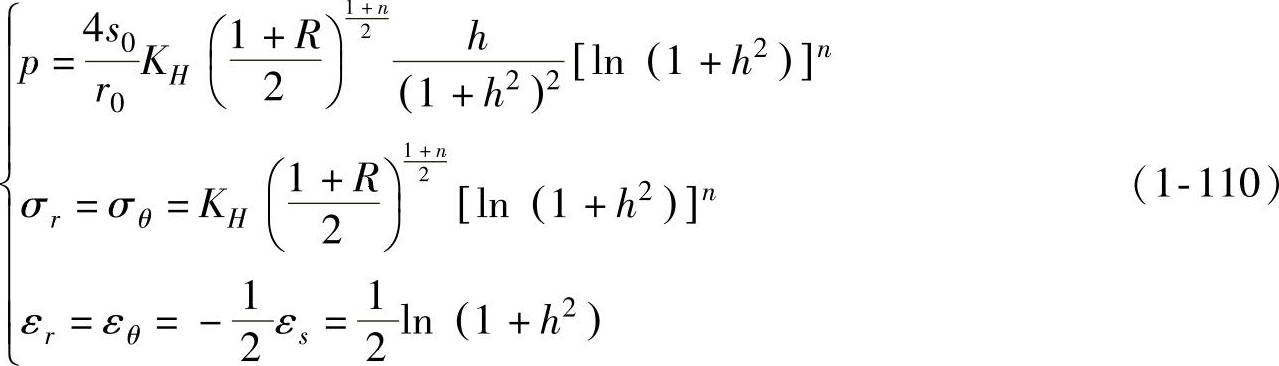
只有当胀形压力p与时间t的关系给定时，应变速率场才能确定。

（2）超性材料的解 对于超塑性材料，将式（1-109）代入式（1-91）可得到胀形高度H（h＝H/r₀，下同）与胀形时间t之间的关系，再代入式（1-107）和式（1-108）可得到用胀形高度H表示的解析解为

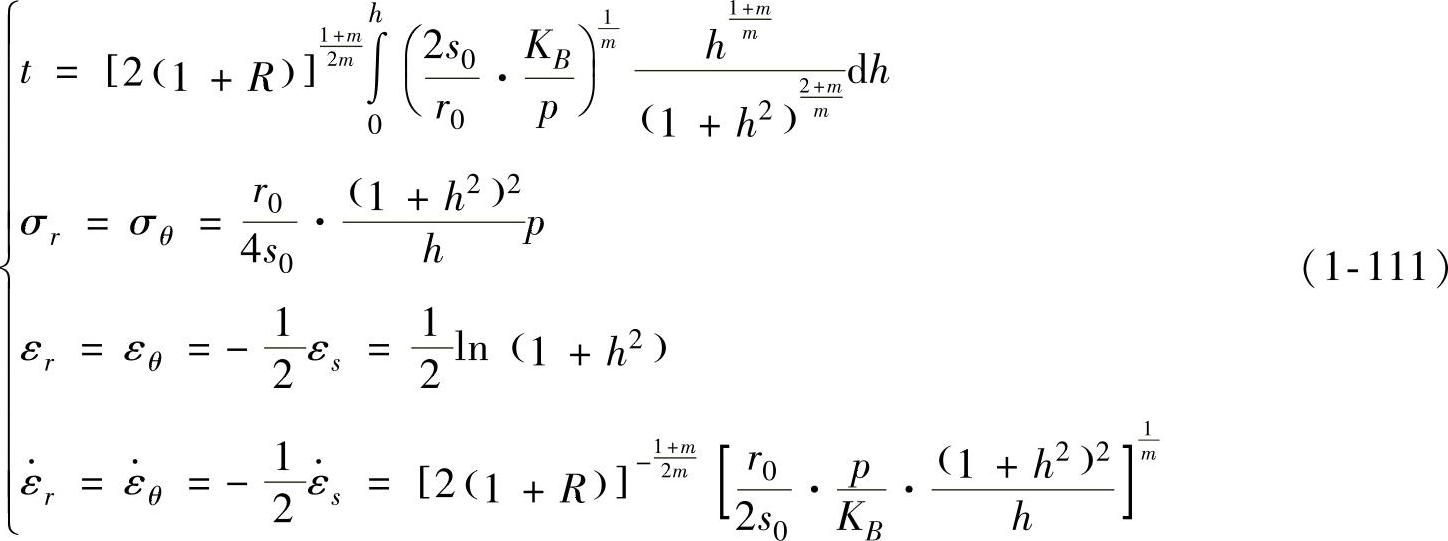
（3）讨论 引入均匀球壳假设，相当于把薄板自由胀形看做内部存在压力源的封闭球壳的变形过程，而薄板自由胀形是由平板成为空间壳体，两种变形的质点位移不相同，所以上述解不满足约束方程式（1-103），因而也不满足几何方程式（1-79）和式（1-80）。

3.不均匀球壳假设条件下的解析解

假设胀形的任一时刻轮廓形状均为球壳的一部分，但球壳的厚度分布是不均匀的。由式（1-105）可知，球壳的曲率半径为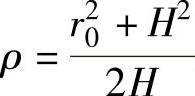。将式（1-105）代入式（1-97）可得F＝1，再代入式（1-100）可得G＝1，因此，式（1-103）变为

考虑边值条件式（1-104），求解该微分方程可得

由此可得质点瞬时坐标与原始坐标及胀形高度之间的关系为

将式（1-114）代回式（1-79a）～式（1-82），并将应变分量对时间求导可得不均匀球壳在假设条件下的解析解为

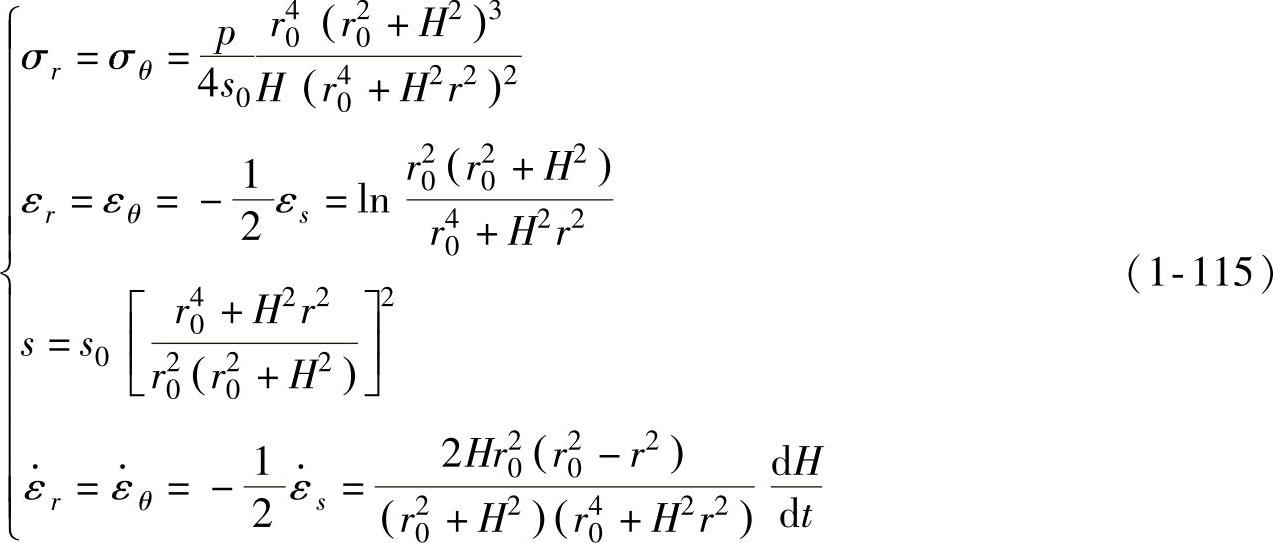
用质点的瞬时径向坐标表示上述结果则有

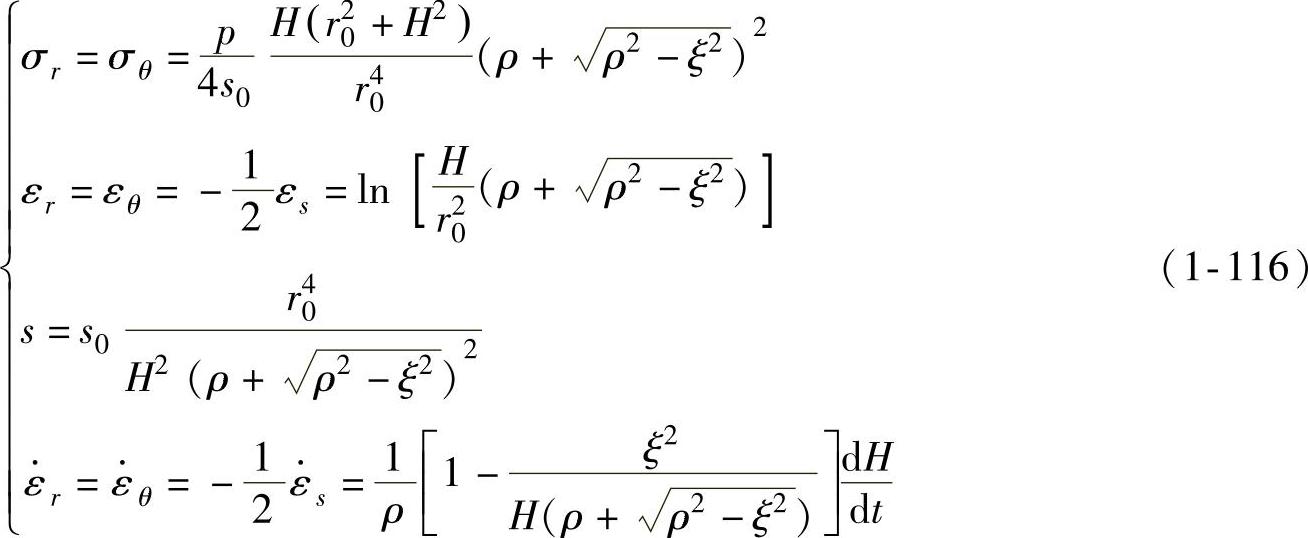
当胀形高度超过半球时，用质点的瞬时纵向坐标表示上述结果更为有利。为此，令h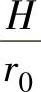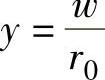＝，，则有

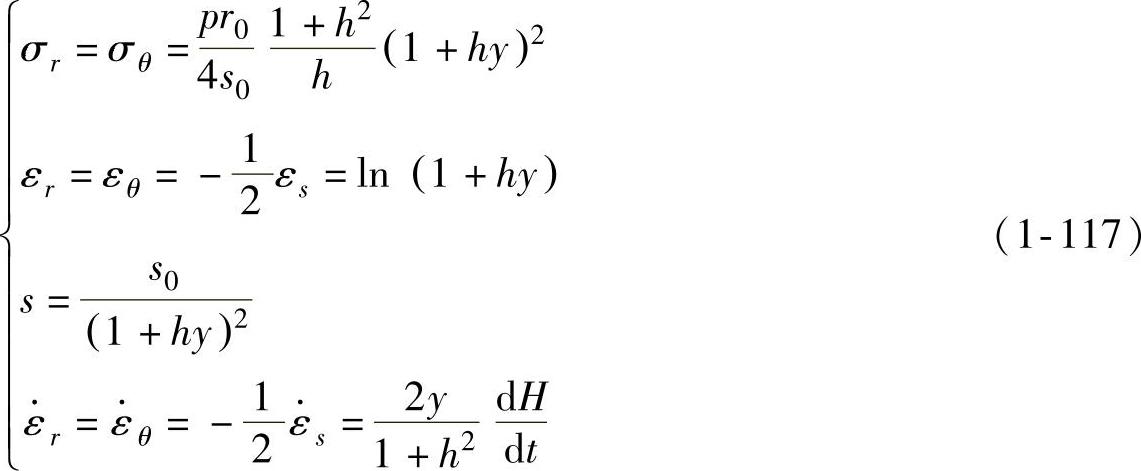
在胀形极点，即对称轴处，ξ＝0，将此值及式（1-117）代入式（1-88）～式（1-90）可得

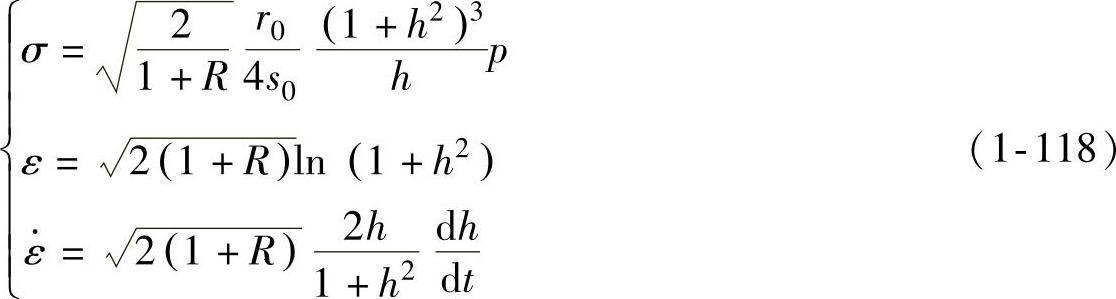
（1）常规塑性材料的解 将式（1-118）代入式（1-92）可得胀形压力p，再代回式（1-117）可得

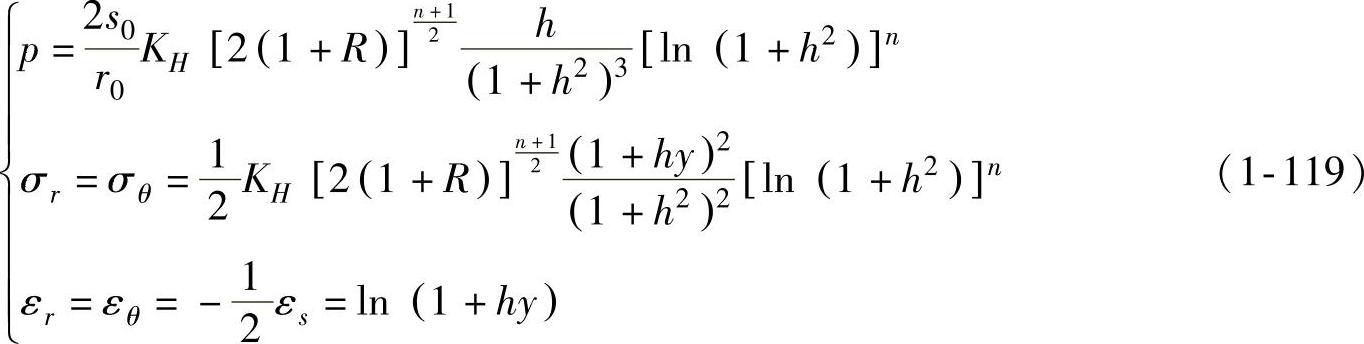
（2）超塑性材料的解 将式（1-118）代入式（1-91）可得胀形高度H（h＝H/r₀，下同）与胀形时间t之间的关系，再代回式（1-117）可得到解析解为

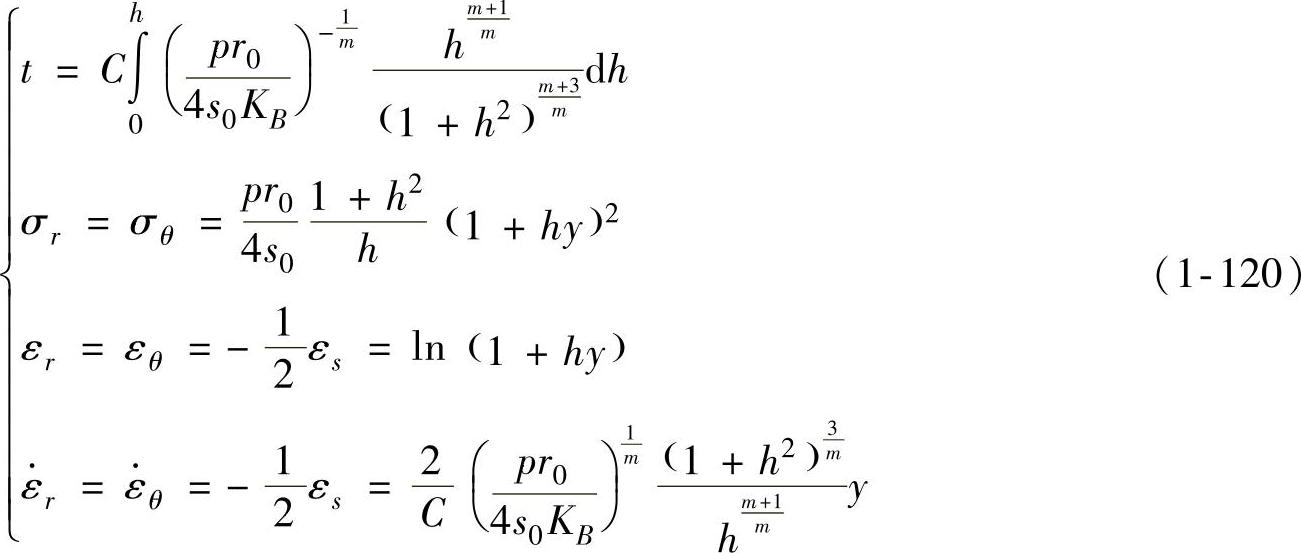
其中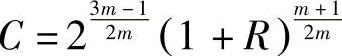

（3）讨论 不均匀球壳假设虽然考虑了厚度的变化，比均匀球壳假设前进了一步，但仍存在明显的问题：①无论是常规塑性材料还是超塑性材料，厚度分布相同；②仅在胀形极点处满足本构方程，其他变形质点均不满足。所以，仅在胀形极点附近上述结果才有意义，可以用来进行极限分析。