轴对称薄板自由胀形解析的理论基础

如图1-15所示，尽管图中引入了表明质点应变、应变速率及应力主轴的随动坐标τ、θ、n，但为了统一，上述3个张量主分量的下脚标仍用r、θ和s表示。前文已给出推导过程，此处不再重复介绍。

1.轴对称几何方程

变形前位于A处的质点变形后位于B点（见图1-15）根据对数应变的定义及几何关系可得到切向应变

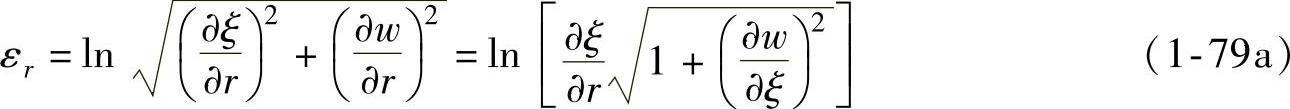
由式（1-78）又可推导出

周向应变及法向应变可由基本概念直接给出，即

2.轴对称平衡方程

（1）轴向平衡（推导过程略）

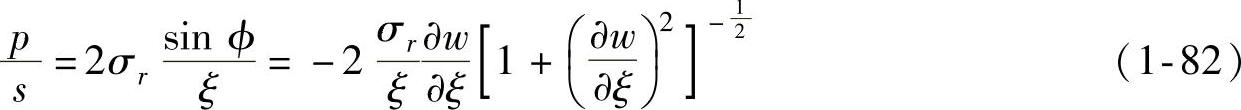
（2）切向平衡（推导过程略）

（3）法向平衡 法向平衡方程即为无矩薄壳理论中著名的拉普拉斯方程（推导过程略），即

其中，ρ_r和ρ_θ为胀形轮廓子午剖面B点处的曲率半径和胀形轮廓过随动坐标n轴并垂直于子午面剖面上B点处的曲率半径。它们分别为

3.物理方程(www.xing528.com)

（1）塑性流动理论 对于轴对称平面应力问题，根据R.Hill关于各向异性材料的经典塑性理论，同时考虑面内同性、厚向异性时应有

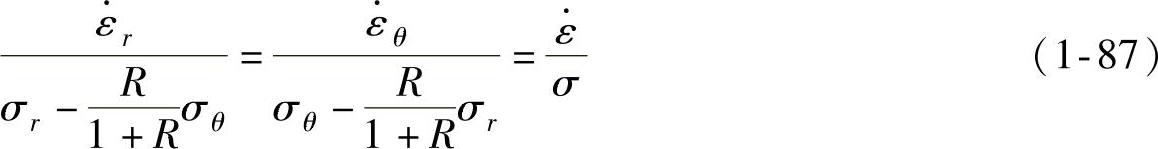
式中 R——板材的厚向异性系数。

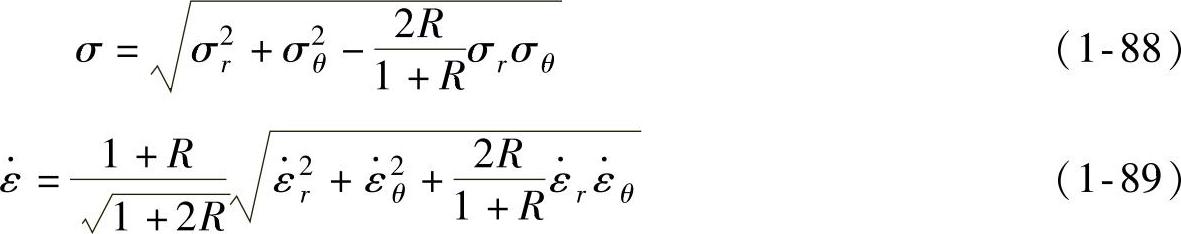
此外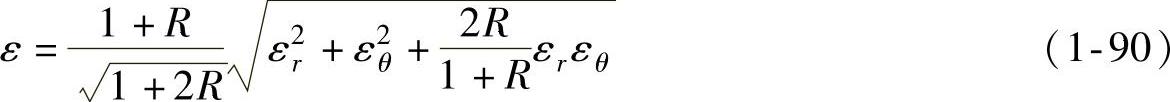

σ、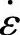和ε分别为等效应力、等效应变速率和等效应变。

经典塑性理论认为，塑性变形时应力张量主轴总是与应变增量张量（或应变速率张量）主轴重合的，复杂应力状态下应力张量主轴不一定与全量应变张量的主轴重合。如前所述，轴对称薄板自由胀形时，σ_ij、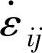和ε_ij三个张量的主轴始终重合。此时，等效应力σ与等效应变速率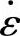之间或等效应力σ与等效应变ε之间的关系满足单向拉伸时的本构方程。

（2）超塑性材料单向拉伸时的本构关系 超塑性材料是对应变速率敏感的，描述其本构关系最常用的是Backofen方程，即

式中 K_B——材料常数；

m——应变速率硬化指数。

（3）常规塑性材料单向拉伸时的本构关系 常规塑性材料是对应变敏感的，常用Hol-lomon公式来描述，即

σ＝K_Hεⁿ （1-92）

式中 K_H——材料常数；

n——应变硬化指数。

（4）考虑两种敏感性并存时的本构关系Rosserd的粘塑性方程考虑了两种硬化并存情况，即