轴对称薄板自由胀形的几何和力学特点

纵观塑性理论的研究历史，试验研究或实验验证的方法除单向拉伸、单向压缩外，大多采用薄壁管拉扭复合加载和薄板自由胀形，而对于复杂应力状态下的塑性理论问题，必须采用后两种试验方法。如图1-15所示，轴对称薄板自由胀形具有下列显著特点：

1）由于是轴对称问题，胀形前毛坯又是平板，所以仅用一个径向坐标r就可以完整地描述质点的几何位置。

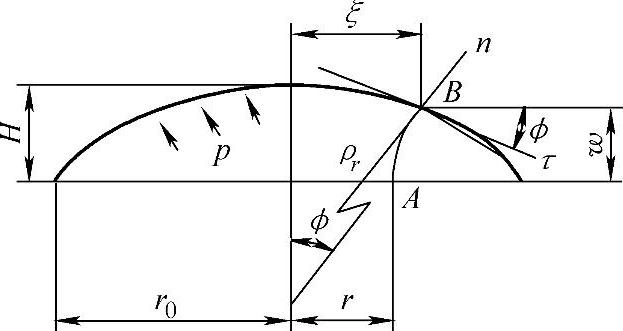
图1-15 轴对称薄板自由胀形示意图

2）胀形开始后，平板毛坯变为空间壳体，但由于是轴对称问题，胀形轮廓和质点的运动轨迹均可表示在一个子午剖面内，如图1-15所示。质点的位置可用瞬时坐标ξ和w表示，也可用ξ和ϕ表示，还可用ξ和ρ_r表示。后两种均为间接表示。胀形极点高度是时间的单值函数，H＝H（t），因此可作为胀形时间的间接度量参数。

3）薄板胀形时表面积的增加靠板厚的不均匀变薄来补偿，变形区是确定的，即为直径为2r₀的原始毛坯。板面内是双向伸长应变，板厚方向是压缩应变。应变主轴的方向是随胀形过程的进行而不断变化的。但由于是轴对称问题且受力状态简单（见后述），应变主轴的方向与胀形轮廓的变化有明确的关系，即质点所在位置胀形轮廓子午剖面的切线方向τ、法线方向n及周向θ是3个应变主方向。如图1-15所示，可以3个主轴建立随动坐标，其位置由（ξ，w）确定，其空间方位由ϕ确定。由此可见，求解薄板自由胀形的变形过程，最终就是要确定质点的瞬时坐标与原始坐标及胀形高度之间的关系，即

ξ＝ξ（r，H），w＝w（r，H） （1-75）

消去H便可得到表示胀形中质点运动轨迹的方程，即(www.xing528.com)

f（ξ，w，r）＝0 （1-76）

若消去r，便可得到不同胀形高度时的胀形轮廓方程，即

g（ξ，w，H）＝0 （1-77）

由式（1-77）又可确定随动坐标的空间方位，即

4）由上述分析可知，以随动坐标表示的3个应变主轴中，θ主轴的方向始终不变，τ和n两个主轴随胀形轮廓的变化而在子午剖面内改变方向。应变速率的概念是应变分量对时间的变化率，由于是轴对称问题，θ方向必定也是应变速率的一个主方向，且该主方向始终不变。对于薄板问题，厚度方向必定是应变速率的另一个主方向。根据张量的性质，第三个应变速率主方向则必定是胀形轮廓子午剖面的切线方向。所以，在薄板自由胀形过程中，质点的应变主轴与应变速率主轴始终是重合的。

5）薄板自由胀形的受力状态简单，唯一的外载荷是均布的胀形压力p，不存在摩擦因素。塑性成形中的摩擦无论是理论研究还是实测方法均不完善。自由胀形避免了摩擦的影响，质点的应力状态仅取决于材料本身的性质和胀形压力。薄板问题又可作为平面应力考虑，所以，薄板自由胀形属于板面内的双向拉应力状态。考虑到问题的轴对称性，图1-15中的随动坐标同时也是质点应力状态的主轴坐标。至此可得出结论：薄板自由胀形过程中，应变主轴、应变速率主轴及应力主轴三者始终重合。