双向拉伸失稳理论详解

1.基本方程

根据R.Hill的各向异性塑性理论，仅考虑厚向异性时有

其中

则

由式（1-53）可得

用式（1-57a）和式（1-57b）除以上式，再用式（1-56）除以上式，注意到，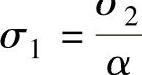

则有

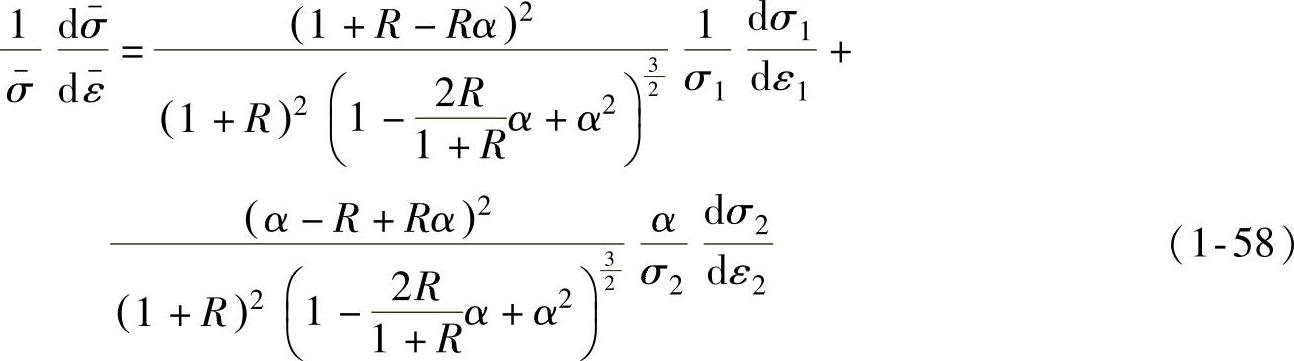
假设材料的应力应变关系符合幂次式，即

则

上述各式即为推导失稳应变的基本方程。

2.平板双拉的载荷失稳

平板受双向拉伸的情况如图1-12所示。

由应力、应变的定义可知

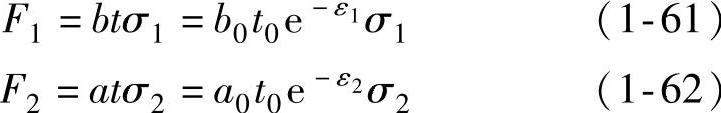
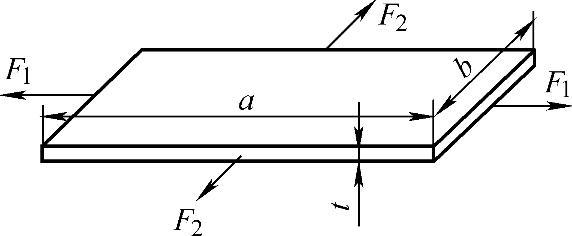
图1-12 平板受双向拉伸的情况

（1）Dorn准则——dF₁＝0由式（1-61）可推导出，即

(www.xing528.com)

将式（1-63）代入式（1-58）和式（1-60），注意到，且在简单加载时α＝const，dσ₂＝αdσ₁，化简后可得

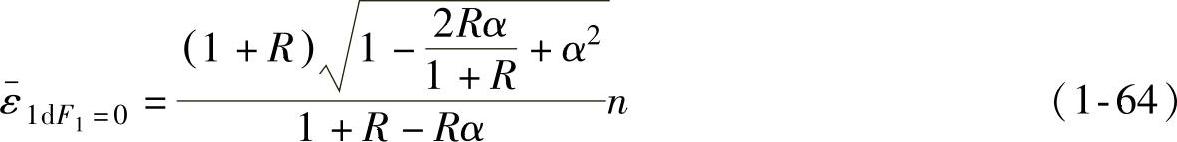
（2）Swift准则——dF₁＝dF₂＝0由式（1-61）和式（1-62）可将此准则表达为

将式（1-65）代入式（1-58）和式（1-60）化简后可得

式（1-66）则为Swift理论给出的产生分散性失稳时的等效应变。

3.平板双拉的集中性失稳

双向拉应力状态（0＜α≤1）下的板料，其应变状态也有两种可能，如图1-13所示。

1）拉-压状态：

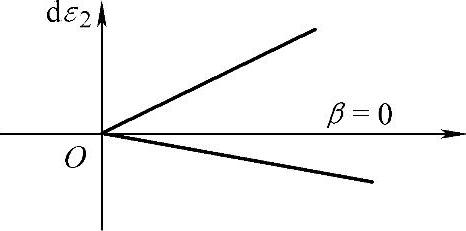
图1-13 双向拉应力对应的应变状态

2）拉-拉状态：0≤β≤1。

在拉-拉应变区不存在应变零线，失去了产生集中性失稳的前提，则Hill的集中性失稳理论失效。1967年，波兰学者马辛尼克（Z.Morciniak）和库祖斯基（K.Kuczyski）为了解决准则与实际之间的分歧，提出了一种凹槽假说，文献中称为M-K理论，但此理论尚不完善。

在拉-压应变区，集中性失稳产生的条件是：板面内必须存在一条应变零线，且在这种条件下，板料厚度的减薄率（软化因素）恰好可由板料的强化率得到补偿，凹槽才得以产生、发展。设凹槽的方位是y，与式（1-51）的推导类似，则有

由式（1-57）可得

显然，处于平面应变状态时（β＝0，或），θ＝90°，槽与1轴（图1-11中）垂直。如果β＞0或，即超过平面应变的双拉状态，则式（1-67）无解。

当应力状态在单向拉伸和平面应变之间时（，≤β≤0），板面内有应变零线存在。当板料达到某一变形程度时，材料的强化率与厚度的减薄率恰好相等，凹槽开始出现集中性失稳（满足Hill理论），此时

将式（1-57c）和式（1-60）代入式（1-69），即可得到产生集中性失稳时的等效应变，即