单向拉伸失稳理论简析

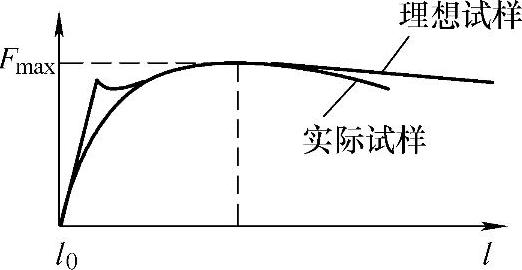
图1-10 单向拉伸曲线

1.载荷失稳

假设一理想均匀板条，其原始长度为l₀、原始宽度为w₀、原始厚度为t₀，在拉力F作用下产生塑性变形，变形后板条的各尺寸分别为l、w、t。设材料面内同性、厚向异性，厚向异性系数为r，从试件的承载能力看，当F＝F_max时，材料已经作出了最大的贡献，外载荷不可能再有所增加，通常把这种现象称为载荷失稳，单向拉伸曲线如图1-10所示。此时有

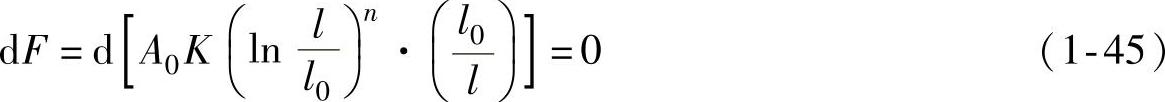
其中，A₀＝w₀t₀，A＝wt，。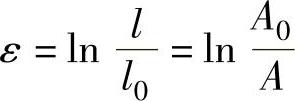

载荷失稳条件为

载荷失稳时的应变为

ε₁＝n （1-47）

2.变形失稳

加载失稳以前，理想均匀板条和实际板条的变形行为基本一致。但从板条形状变化的角度看，理想均匀板条遵循宏观塑性力学的规律，应保持均匀变形，即沿着板条长度方向，轴向伸长与剖面收缩完全一致。而实际板条则不能保持均匀伸长，出现缩颈，变形局限在缩颈区内发展，曲线段较短。从变形的角度看这也是一种失稳现象。

（1）分散性失稳 加载失稳以后，缩颈在板条的较大一个区间内扩展，称为分散性失稳。根据试验观察，板条单向拉伸时，外载荷的加载失稳点和变形的分散性失稳点基本同时出现。所以，单向拉伸的分散性失稳条件也是式（1-46），或可表达为（Swift失稳理论）

式（1-48）可解释如下：因为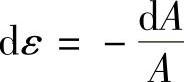，所以材料的强化率恰好等于断面的减缩率。故分散性失稳又可称为宽向失稳。(www.xing528.com)

（2）集中性失稳 分散性失稳的缩颈扩散发展到一定程度后，变形集中在某一狭窄条带内（与板厚为同一数量级），发展成为沟槽，称为集中性失稳。集中性失稳开始以后，沟槽加深，外载急剧下降，板条最后分离为两部分。集中性失稳产生的条件是：材料的强化率与其厚度的减缩率恰好相等。这就是R.Hill的集中性失稳理论，即

故集中性失稳也可称为厚向失稳。

因为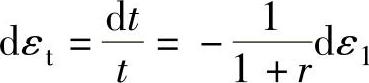，所以可求得单向拉伸集中缩颈开始发生时的应变为

ε₁＝（1＋r）n （1-50）

（3）集中缩颈的方位 分散性失稳发展到一定阶段，实际板条的最薄弱环节开始集中在某一狭窄条带内，发展成为沟槽。沟槽的发生、发展主要依靠板料的局部变薄，而沿沟槽没有长度的变化，即dε_y＝0（见图1-11），所以有

dε₁cos²θ＋dε₂sin²θ＝0

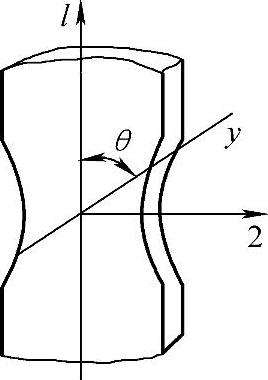
图1-11 集中缩颈示意图

单向拉伸时，因为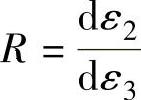，dε₁＋dε₂＋dε₃＝0，所以有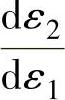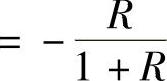，故此可得

对于各向同性材料，r＝1，θ＝54°44′。材料的单向拉伸试验已证实了该结论。

单向拉伸失稳理论是讨论板材在双向受力而以受拉为主的变形方式下变形失稳问题的基础。但是还有许多问题有待深入研究。由于几何尺寸与材料性质不均，实际板条加载失稳时产生分散性缩颈，其起始部位具有随机性。缩颈区内因应变速率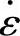与应变比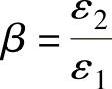的变化产生的强化效应，可获得缩颈区内亚稳定流动条件，这决定了分散缩颈的范围大小与集中缩颈的出现时刻。