同性厚板与异性薄板的平面应力问题

1.屈服准则

设σ_s为板材的面内单向拉伸屈服应力，σ_ts为板材厚度方向的单向拉伸屈服应力，τ_s为板材的面内剪切屈服应力。因为面内同性，即F＝G，所以X＝Y＝σ_s，另外有Z＝σ_ts，T＝τ_s。将平面应力条件和面内同性条件代入式（1-13），得

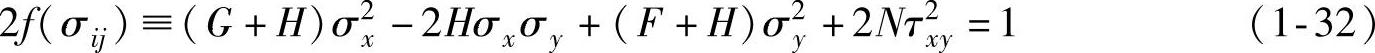
由式（1-32）和式（1-14）可得

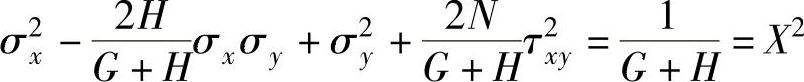
令

R称为板厚方向性指数，或简称为厚向异性系数。因为N＝F＋2H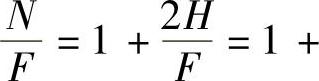，2R，所以

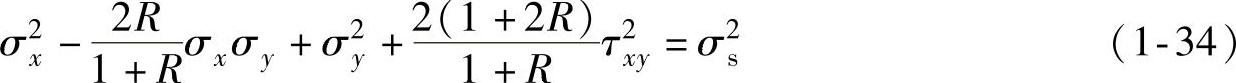
在主轴坐标下

此外，因为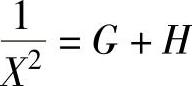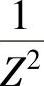，＝F＋G，所以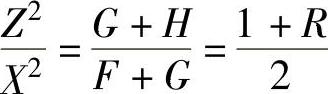，即

或

式（1-37）表明：R值虽然由应变比定义引入，但它本质上反映的是面内同性厚向异性板材面内屈服应力与厚向屈服应力的差异。当R＝1时，为各向同性材料。

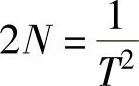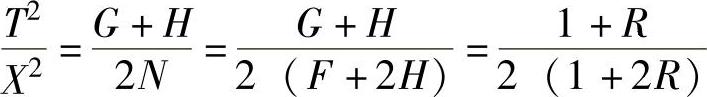又因为，所以，即

可见，对于平面应力状态下的面内同性厚向异性薄板成形问题，不仅屈服准则大大简化，而且4个试验参数X、Y、Z、T减少为两个板材性能参数σ_s和R，它们均可通过一个单向拉伸试验获得，避免了试验确定σ_ts和τ_s所遇到的困难。

当R＝1时为各向同性板材，此时，。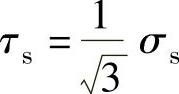

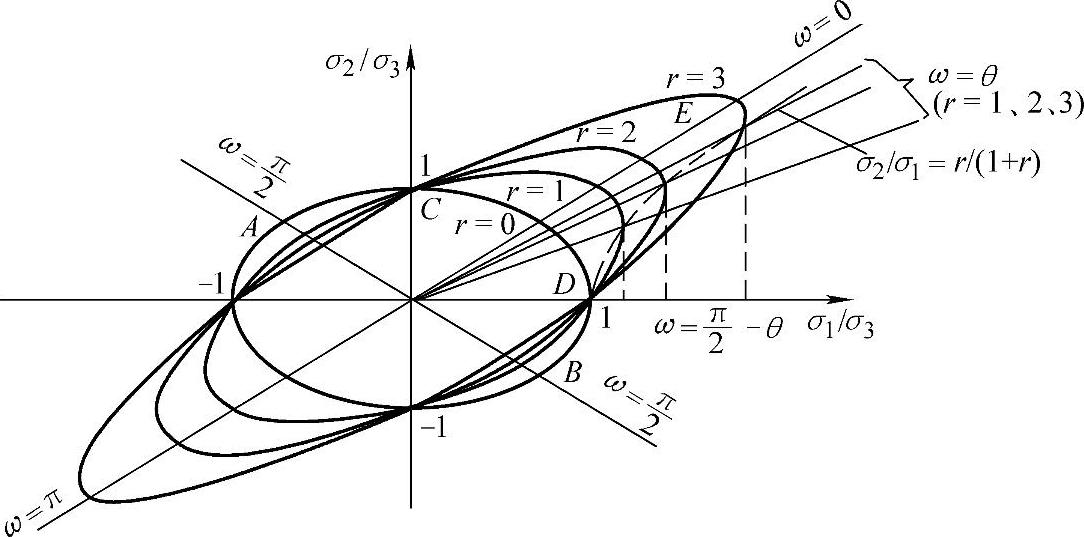
图1-9 厚向异性薄板的屈服轨迹

式（1-34）和式（1-35）给出了平面应力条件下面内同性厚向异性薄板的屈服准则。图1-9所示为在主轴坐标下按式（1-35）作出的厚向异性薄板的屈服轨迹——椭圆族，明显地表示出了厚向异性对于材料屈服的影响：材料的厚向异性系数R越大，椭圆的长轴越长，短轴越短。所以R值大的材料不仅具有较强的变薄抵抗力，而且同号应力状态下变形抵抗力大。所以拉伸时危险断面的强度高，而异号应力状态下变形抵抗力小，有利于剪切或拉伸法兰区的变形。

经过变换，式（1-35）也可以用参数角ω表示为

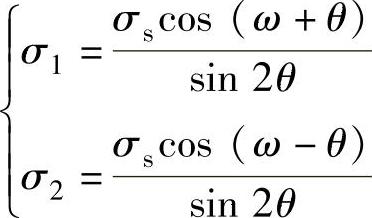
式中 θ——厚向异性参数角，。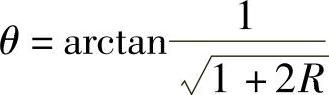

参数角ω可用于表示板面内的主应力状态。例如在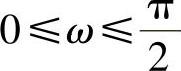的象限内：

当ω＝0时，σ₁＝σ₂，为双向等拉应力状态；

当ω＝θ时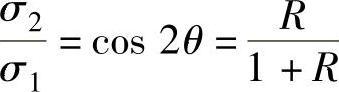，，为平面变形应力状态；

当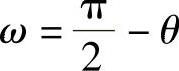时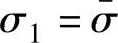，，σ2＝0，为单向拉伸应力状态；

当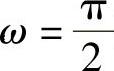时，σ₂＝-σ₁，为纯切应力状态。

其余象限可依此类推。总之，若以AB为分界线，板材的应力状态在AB的右上方，当-π/2＜ω＜π/2时，就绝对值而言，拉应力大于压应力，应力状态以拉为主，板材的变形特点是厚度减薄；在AB的右上方，当π/2＜ω＜3π/2时，就绝对值而言，拉应力小于压应力，应力状态以压为主，板材的变形特点是厚度增厚。

2.应力应变关系

面内同性厚向异性薄板平面应力问题的应力应变关系可采用类似于第1.3节的方法获得。因为N＝F＋2H＝G＋2H，由式（1-32）可知其加载函数为

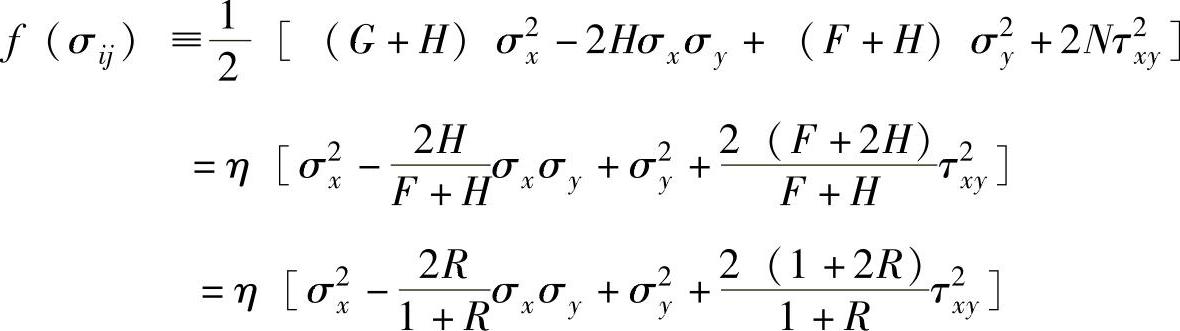
其中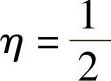，（F＋H）为材料常数。设厚向异性薄板的加载函数f（σ_ij）与等效应力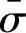之间有以下关系，即(www.xing528.com)

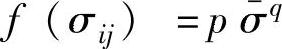
沿x方向单向拉伸时，σ_y＝τ_xy＝0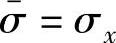，，则f（σ_ij）＝ησ²_x＝pσ_x^q；沿y方向单向拉伸时，σ_x＝τ_xy＝0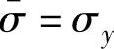，，则f（σ_ij）＝ησ²_y＝pσ_y^q。所以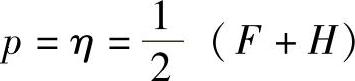，，q＝2，等效应力可定义为

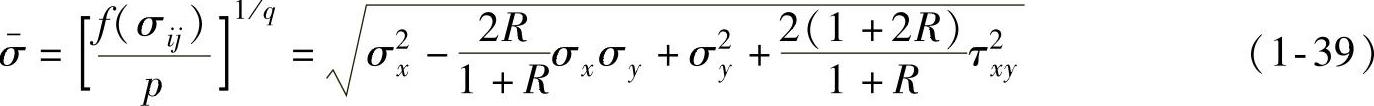
利用厚向异性薄板的屈服准则，由式（1-17）可得应变增量各分量为

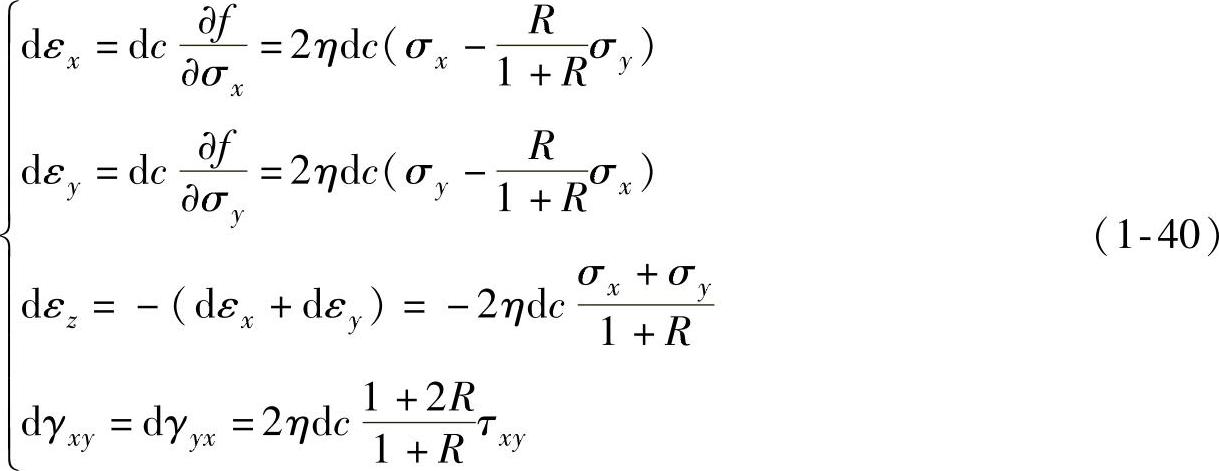
其中，2ηdc可根据等比定理按如下方法推得。由式（1-40）可得

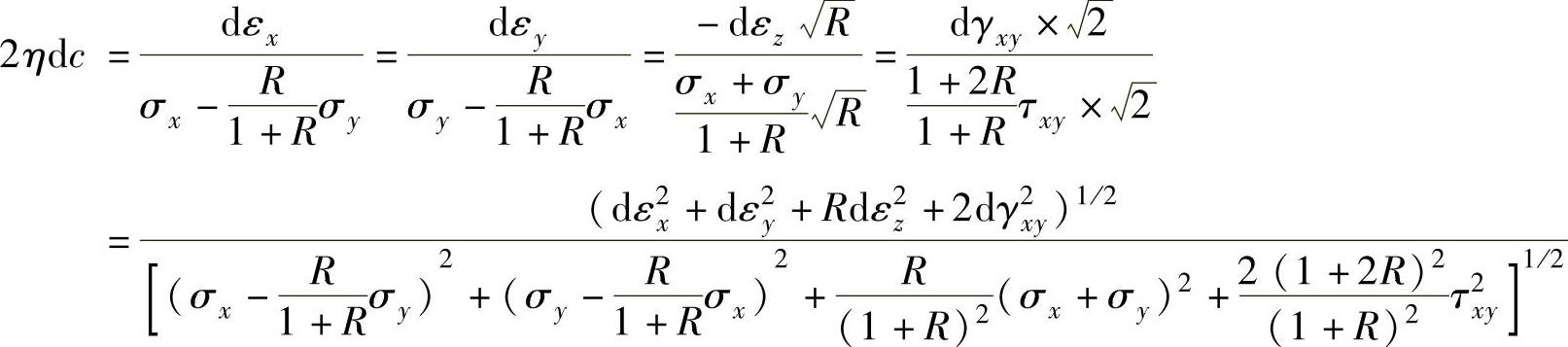
因为

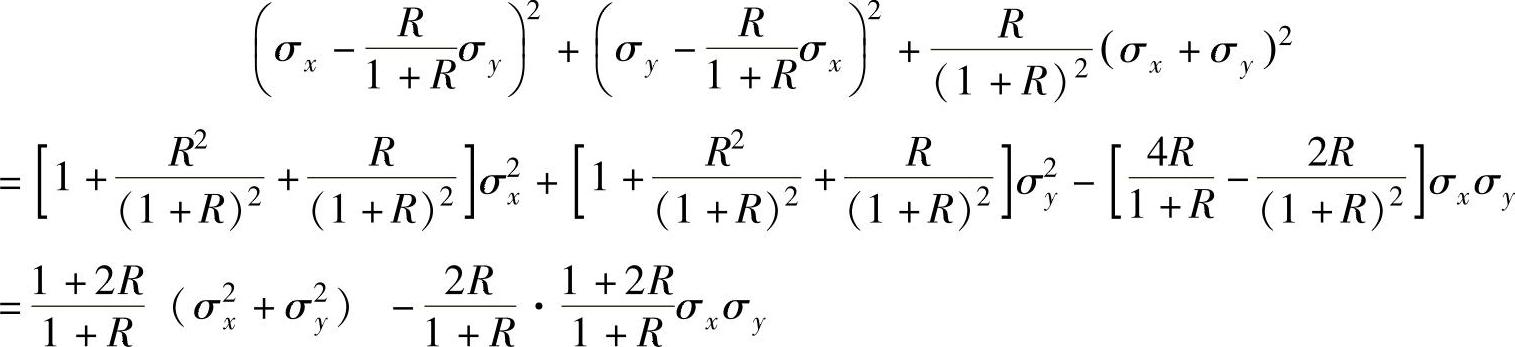
又因为

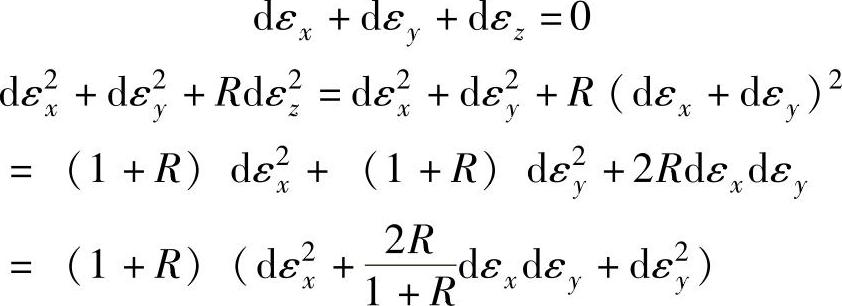
所以

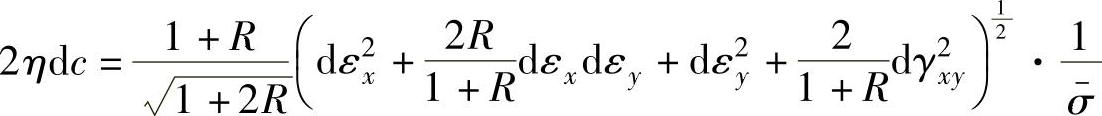
因为单位体积内的塑性变形功可以表示为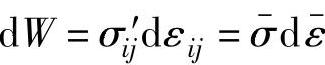，所以

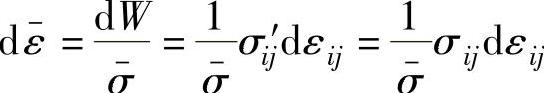
而

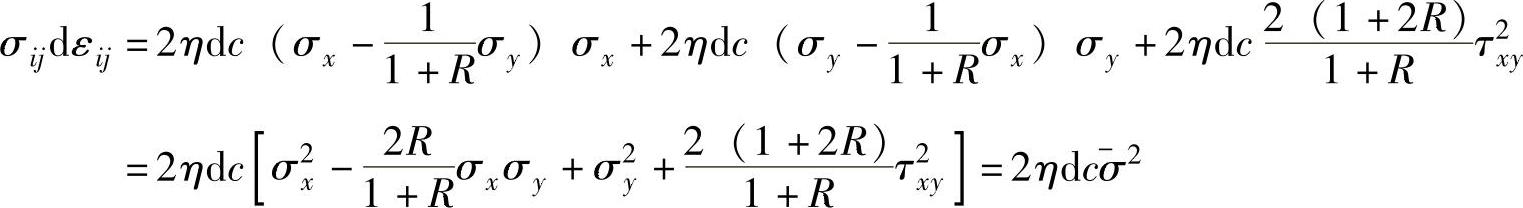
因此可得

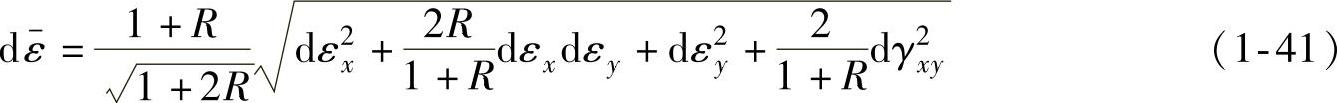
即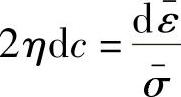，将此关系代入式（1-40），可得

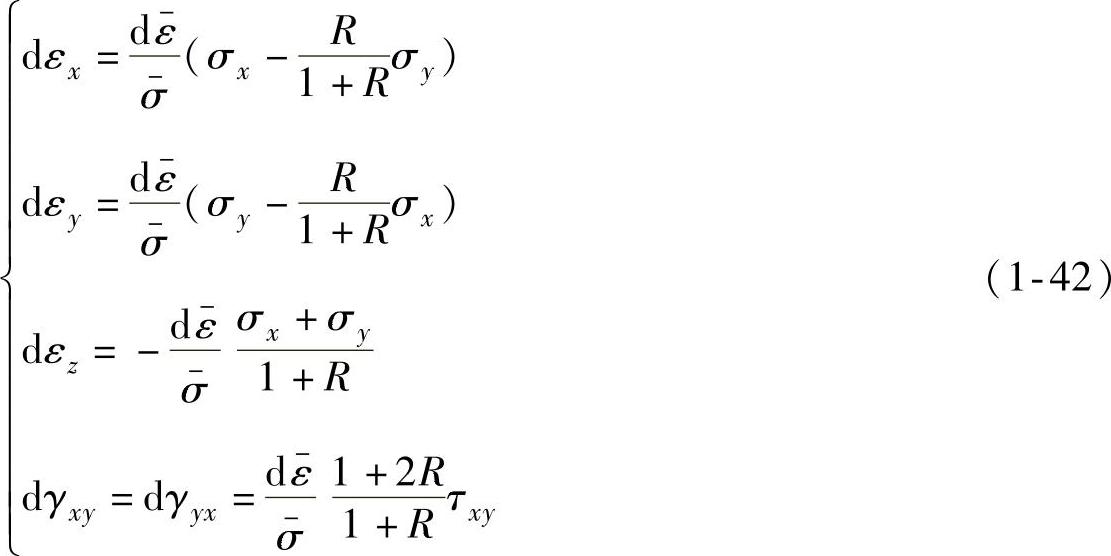
简单加载时，全量应变与应变增量主轴重合且方向不变，对式（1-42）进行积分，可得用全量应变表示的应力应变关系为

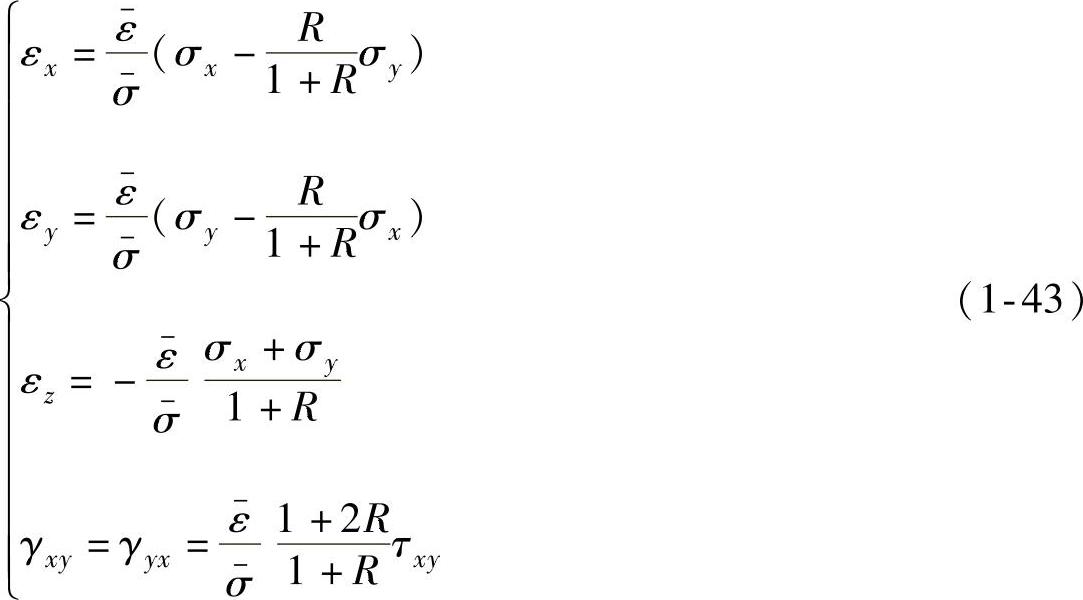
其中

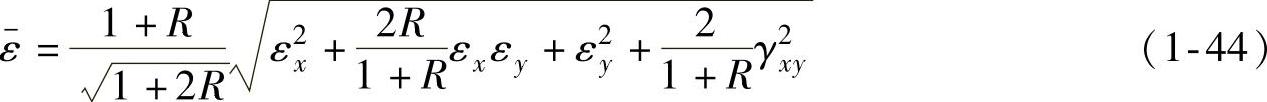
如果将平面应力条件σ_z＝τ_yz＝τ_zx＝0和面内同性条件N＝F＋2H＝G＋2H以及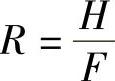直接代入式（1-25）和式（1-26），则有

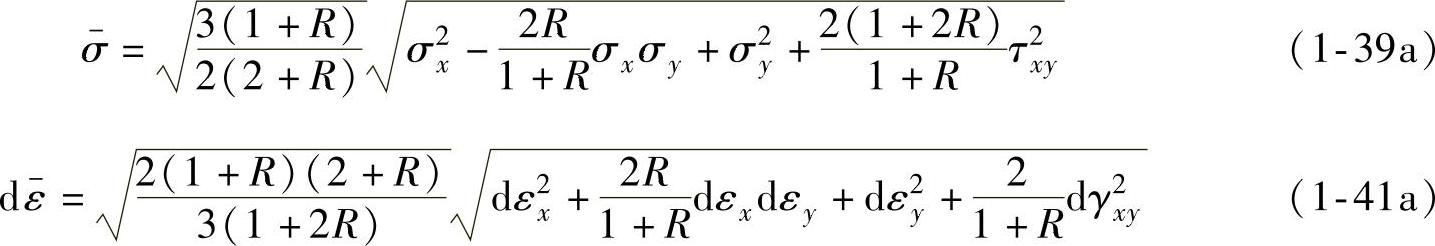
将上述条件和关系式代入式（1-28），结果与式（1-42）完全相同。

应特别指出，等效应力和等效应变增量的两种定义式是不同的，式（1-39a）和式（1-41a）也不直接等于单向拉伸时的应力和应变增量，各自相差一个关于R值某种组合的系数。但是，它们所给出的单位体积塑性变形功增量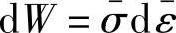相同，所以最终给出的应力应变关系式相同。鉴于此，板材成形塑性理论中均采用式（1-39）～式（1-44），可以直接引入单向拉伸时应力应变的关系给出。

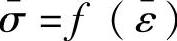利用式（1-42）和式（1-43），可以立即得到以下几点结论：

1）单向拉伸时，如果取l、b、t分别为拉伸试件的长度方向、宽度方向和厚度方向，则有σ_x＝σ_t，σ_y＝τ_xy＝0，ε_x＝εl，εy＝εb，εz＝ε_t，γxy＝0。由式（1-43）可知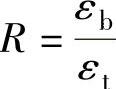，，即厚向异性系数R恰为试件宽向与厚向应变之比，这是由厚向异性应力应变关系决定的。

2）复杂应力状态时，由式（1-42）可知，因为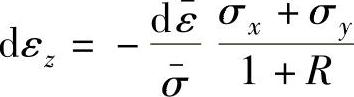，所以，R值越大，则|dε_z|越小，即厚度方向的变形越小。

3）复杂应力状态时，由式（1-42）可知，如果σ＝max{|σ_x|，|σ_y|}＞0，则dε_z＜0；如果σ＝max{|σ_x|，|σ_y|}＜0，则dε_z＞0。即如果面内绝对值大的正应力为拉应力，则板坯减薄；如果面内绝对值大的正应力为压应力，则板坯增厚。