深入解析1.5.3各向异性流动理论

设各向异性体的各向异性主轴为x、y、z。在同一坐标系中，其应力状态为

其应变增量为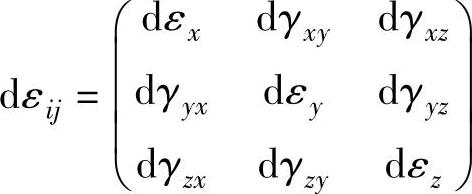，其中dγ_ij＝dγ_ji （1-22）

且应变增量dε_ij与位移增量du_i之间满足以下几何方程，即

如果材料服从R.Hill的各向异性屈服准则[见式（1-14）]，则有

代入式（1-17）得

应注意：dε_x＋dε_y＋dε_z＝0是一个恒等式（体积不变条件），并且如果应力反向的话，应变增量也反向；另外，如果应力主轴和各向异性主轴重合，那么应变增量主轴也和各向异性主轴重合，否则，应力和应变增量主轴一般是不重合的。

若希望通过试验来确定各向异性的状态，则要求在足够大的体积内各向异性的分布是均匀的，使能在其中的任意方向上切取拉伸试件。于是，如果有一单向拉应力X作用在沿平行于各向异性x主轴所切取的一个长条或圆柱试件上时，其应变增量的比例为

dε_x∶dε_y∶dε_z＝（G＋H）∶-H∶-G

可见，在每一横断面方向上的应变是收缩的，除非屈服应力的差非常大，以致G或H中有一个量为负。如果H﹥G，也即Z﹥Y，则在y方向的收缩是较大的；因此，在屈服应力较大的方向上应变较小。同样，在y和z方向上的拉伸试验可得到比值F/H和G/F。在理论可以应用的情形下，在沿着x和y方向切取的拉伸试件上量度应变比值，并借助式（1-15）来确定3个拉伸屈服应力比值的间接方法；如果屈服现象不显著，这样做要比直接方法更好。对于薄板材料，通过这种方法来决定厚度方向上的屈服应力特别方便。

为了确定式（1-24）中的比例系数dc值，必须设法将它与单向拉伸应力应变曲线联系起来。与各向同性材料塑性理论的处理方法相仿，对于一般应力状态下的各向异性材料也要定义一个与单向拉伸等效的等效应力和等效应变。

等效应力的定义方法如下：

1）等效应力是一个决定材料塑性流动是否发生的量，所以可以假定加载函数f（σ_ij）与等效应力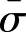之间有以下关系，即

式中，p、q均为常数。

2）等效应力又可作为一个可比指标，将一般应力状态等效地简化为单向拉伸状态下的应力。单向拉伸时，设x轴为拉伸方向，则σ_x＝X，σ_y＝σ_z＝τ_xy＝τ_yz＝τ_zx＝0，此时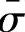＝σ_x＝X，又因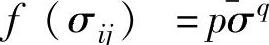，则可得

显然有

同理，取σ_y＝Y，σ_x＝σ_z＝τ_xy＝τyz＝τzx＝0，此时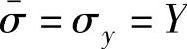，可得

取σ_z＝Z，σ_x＝σy＝τ_xy＝τyz＝τzx＝0，此时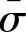＝σ_z＝Z，可得(www.xing528.com)

则有

所以，等效应力为

定义等效应变增量dε-时，可从单位体积的塑性变形功dW考虑。塑性变形功dW可表示为

塑性变形功dW又可表示为

dW＝σ_ij′ dε_ij所以，等效应变增量dε-可表示为

可以证明

所以

其中，dc可由式（1-24）推导出，将式（1-24）的前三式作如下处理，即

将以上三式和式（1-24）的后三式等号两边取平方再乘以相应的各向异性参数，使其等号右侧的应力分量平方项与等效应力定义式（1-25）的对应项相同，即

将上述六式中的前三式除以（FG＋GH＋HF）2后，再将该六式相加，并应用式（1-25），可得

由此得到等效应变增量的定义式为

进而得到dc的表达式为

代入式（1-24）则得

当L＝M＝N＝3F＝3G＝3H时，各向异性流动理论完全退化为各向同性塑性理论中的

Levy-Mises塑性流动方程，即

其中