应力状态分析在1.2.1点的研究

1.应力状态的表达方式

在外力作用下，物体内各质点之间会产生相互作用的力，称为应力。通过一点可有无限个微分面，不同微分面法线方向的应力不同。任意3个相互垂直的微分面的应力可以表示一个确定点的应力状态，而3个微分面的应力需要用9个分量描述；根据切应力互等定理，点的应力状态需要用6个独立的分量描述。这样一点的应力状态的9个分量便构成了张量，张量存在不变量，且含有3个主方向和3个主值。为了研究P点的应力状态，需要3个相互垂直的微分面，并用3个微分面上的应力表示P点的应力状态，如图1-1所示。

2.主应力

如果已知一点应力状态的9个应力分量，则过该点的斜切微分面上的正应力σ和切应力τ都将随外法线的方向余弦l、m、n的变化而变化。任意斜切微分面的应力如图1-2所示。

图1-1 3个微分面上的应力分布

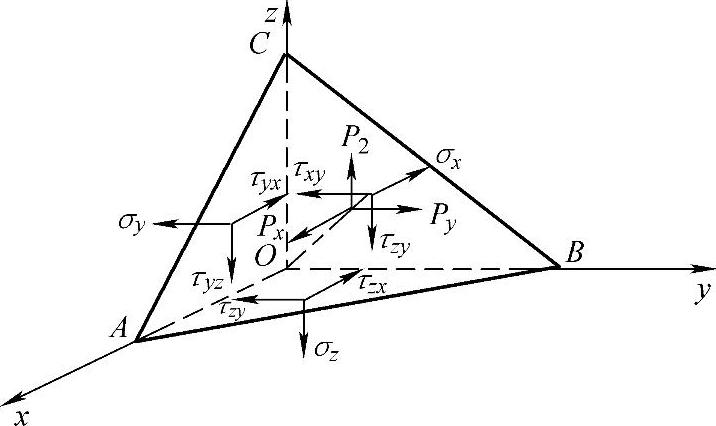
图1-2 任意斜切微分面的应力

当l、m、n在某一组合情况下，斜切微分面上的全应力S和正应力σ重合，而切应力τ＝0。这种切应力为零的微分面称为主平面，主平面上的正应力称为主应力。主平面的法线方向（即主应力方向）称为应力主方向或应力主轴。

3.主切应力

与分析斜切微分面上的正应力一样，切应力也随斜切微分面的方位变化而改变。切应力达到极值的平面称为主切应力平面，其面上作用的切应力称为主切应力。在主轴坐标系下，主切应力平面如图1-3所示。(www.xing528.com)

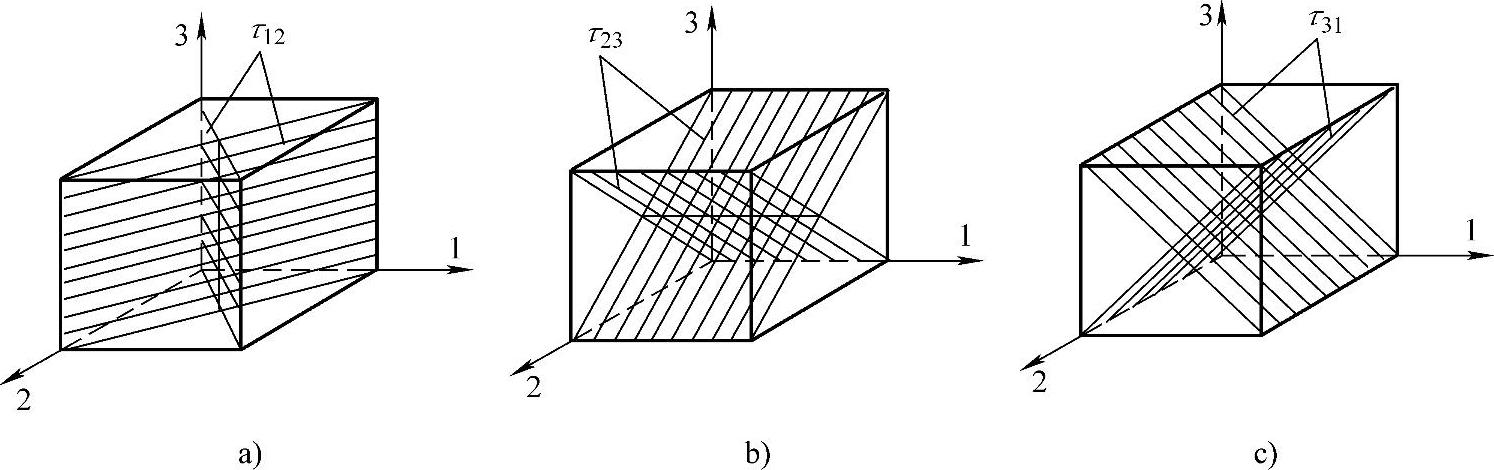
图1-3 主切应力平面

4.应力强度

取八面体切应力绝对值的倍所得的参量称为等效应力，即应力强度。

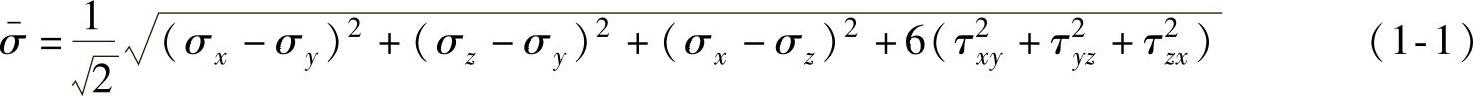
5.应力张量变换关系

在一定的外力条件下，受力物体内部任意点的应力状态已被确定。如果取不同的坐标系，则表示该点的应力状态的9个应力分量将有不同的数值，而该点的应力状态并没有变化。因此，不同坐标系中的应力分量之间应存在以下关系

σ_kr＝σ_ijl_kil_rj（i，j＝1，2，3；k，r＝1，2，3） （1-2）

因此，表示点应力状态的9个应力分量构成了一个二阶张量。