先进树脂基复合材料热氧老化预测模型优化

4.2.3.1　三向正交结构的多尺度几何模型建立

如前文所述，先进树脂基复合材料的热氧老化是一个极其复杂的过程，涉及纤维老化、树脂基体降解以及纤维/基体界面的退化，其中任何一项的改变，对材料的性能都有巨大的影响，而由于老化实验的特殊性，对材料进行常规实验将耗费大量的资源。因此，若能通过有限元模拟的方式来预测复合材料在热氧老化条件下材料的变化并建立相关的模型，不仅能够节约大量资源，还能够对材料进行优化，提高材料的抗老化性能。为此，笔者采用有限元模型研究了热氧老化温度对三向正交机织碳纤维增强环氧复合材料层间剪切性能的影响，具体研究流程如下：

（1）材料制备。T700S-12K和T300S-6K碳纤维混合使用在三维织机上制成三向正交结构预制件，然后真空辅助采用树脂传递模塑成型工艺（Vacuum assisted resin transfer molding, VARTM）将其与JC系列环氧树脂固化成三向正交机织复合材料（3DOWCs）。为了对比分析，制备与三向正交复合材料纤维体积含量一样的二维层合正交复合材料（2DPWCs）。图4-14为两种结构的原理示意图，表4-13为预制件相关工艺参数。

图4-14　三向正交与层合正交结构预制件原理图

表4-13　三向正交与层合正交结构预制件工艺参数

（2）有限元模型的确立。笔者采用有限元法分别在常温（25℃）和高温（150℃）的条件下模拟了3DOWCs的剪切性能，以揭示温度和Z向纱对3DOWCs剪切性能的影响。关于模型的详细信息如下：

①多尺度几何模型。在有限元中模拟中，代表性单元细胞（Representative unit cell, RUC）常被用于与微观结构结合来预测纤维增强复合材料的力学行为。然而，由于双切日剪切试验的特殊性，RUC模型不能用于该实验。基于三向正交机织预制件和环氧树脂的微观几何结构，笔者建立了多尺度（微观尺度、中观尺度和宏观尺度）几何模型来进行该工作，如图4-15所示。复合材料由大量的碳纤维长丝和树脂基体组成，在固化过程中，碳纤维之间的微小空隙被环氧树脂完全填充，因此为了简化该模型，采用由纤维长丝和树脂组成的纤维束，在中尺度单元细胞上建立了等效纤维束的RUC几何模型。然后采用商用ABAQUS软件中的布尔运算得到基体模型。最后，根据试样的尺寸，通过复制单元细胞，进一步得到复合材料的全尺寸模型。然而，全尺寸模型由于元件数量多，模拟剪切过程需要花费大量时间。由于理想的几何模型尺寸的大小对具有相同重复结构的复合材料性能是没有影响的。因此，在研究中就利用小尺寸模型来代表全尺寸模型完成复合材料剪切试验的模拟。

图4-15　3DOWCs的多尺度微观结构几何模型

②材料模型：在材料模型中，碳纤维被认为是与温度无关的材料，表4-14为碳纤维常温（25℃）时的力学参数。而树脂基体的性能在很大程度上依赖于温度，如图4-16所示。

图4-16　高温下环氧树脂的压缩应力—应变曲线

因此，笔者在FEM中假定树脂是受温度影响的材料。根据Haque的研究，计算了不同温度下环氧树脂基纤维束的性能参数，结果如表4-15所示。具体情况如下：高温环境下对环氧树脂基纤维束进行压缩实验，然后从实验结果中提取了载荷—位移曲线的初始斜率。发现除泊松比之外，其他所有弹性性能均被相同的因素影响并下降，通过高温下试样的压缩模量与常温下试样的压缩模量的比值得到下降系数。在本研究工作中，为了模拟复合材料的断裂情况，分别采用韧性破坏准则和剪切破坏准则来控制纤维和环氧树脂的损伤。假定树脂基体是一种各向同性的弹塑性材料，碳纤维束视为横观各向同性材料，并将纤维束与树脂之间的界面视为理想界面。树脂基体和碳纤维二者的柔度矩阵[Sm][Sf]可以分别通过自身材料常数转换得到：

式中：角标m代表树脂基体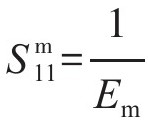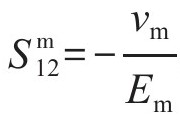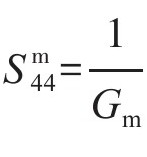，，，；Em和Gm分别为环氧树脂弹性模量和剪切模量；vm为树脂泊松比。

式中：角标f代表碳纤维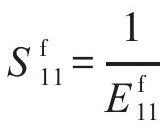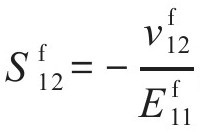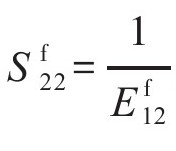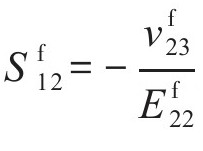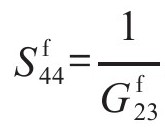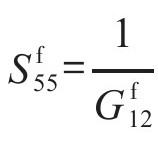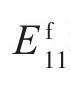，，，，，，；和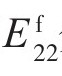分别为碳纤维轴向和径向弹性模量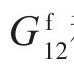；和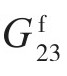为碳纤维剪切模量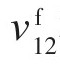；和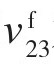为碳纤维轴向和径向泊松比。

表4-14　碳纤维在常温（25℃）时的弹性参数

表4-15　环氧树脂基纤维束在不同温度下的弹性参数

③3DOWCs的双切日剪切试验模型。3DOWCs的双切日剪切试验模型如图4-17所示，图4-17（b）为各构件的详细网格方案，这里没有考虑材料内部缺陷，如空隙等。采用线性六面体单元（C3D8R）对经纱、纬纱进行网格划分；采用C3D8R和C3D6R两种网格对Z向纱进行网格划分。考虑到树脂基体几何结构的复杂性和不规则性，选择了线性四面体单元（C3D4）作为树脂基体。

图4-17　双切日剪切试验模型示意图

（3）模拟分析。笔者采用小尺寸模型计算3DOWCs的双切日剪切失效过程，更直观地了解失效模式。图4-18为3DOWCs、三向正交预制件和环氧树脂基体在常温（25℃）下双切日剪切实验的主要损伤模拟过程，选取6个代表性弯矩来描述实验过程中应力的传递过程。发现在变形达到4.0%之前，应力主要集中在经纱上，这是因为经纱与外力加载方向平行，实验初始阶段它们在应力传递方面起主要作用。当应变达到4.0%左右时，中间的经纱发生破坏，说明试样中出现了纤维断裂。之后，应力集中区域由经纱转移到了Z向纱线上，这意味着随着应变的增加，经纱和Z向纱线分别起到抵抗剪切破坏的作用。这正是3DOWCs表现出明显非线性行为的主要原因（图4-19）。图4-18还显示了剪切试验下基体的破坏过程。根据树脂基体的应力轮廓可知，实验过程中应力主要集中在中间切日区域。树脂的破坏是由相应Z向纱的剪切损伤造成的。从有限元模拟中可以看出，在整个实验过程中3DOWCs依次经历了纤维破坏、树脂基体损伤和材料完全破坏这三个过程。

图4-18　3DOWCs在25℃时的主要损伤过程模拟图

图4-19　3DOWCs在不同温度下的剪切应力—应变曲线

在老化环境下，当温度高于Tg时树脂基体就会失去承载能力，此时复合材料的增强体成为唯一的承载构件，其应力状态和损伤程度对复合材料的整体力学性能有重要影响。为此，笔者选取了高于环氧树脂Tg的老化温度（150℃）进行有限元模拟，来了解高于Tg时材料增强体结构的变化。图4-20即为在150℃下进行剪切实验时经纱和Z向纱的应力分布和传播。图中只观察到经纱的屈曲，这一现象产生的原因归根于树脂基体软化后引起的纱线横向弹性模量与剪切模量的不同。因为在150℃时，纤维束的横向弹性模量为0.137GPa，剪切模量为0.047GPa（表4-15）。因此，3DOWCs在高温下容易受到延性损伤，这一点在材料破坏后的截面图中可以看到[图4-21（d）]。此外，Z向纱的剪切应力随着剪切变形的增大而增大，且主要集中在双切日处。这意味着在树脂基体和纤维/基体界面性能退化的高温环境下，Z向纱有助于材料抵抗外界剪切载荷，也是剪切载荷的作用而使得Z向纱线产生了张力效应。这正是在相同的高温条件下3DOWCs比2DPWCs表现出更高的ILSS和剪切模量的原因（图4-19）。

图4-20　3DOWCs在150℃的主要损伤过程

图4-21　不同温度下3DOWCs的断日形貌(www.xing528.com)

从以上模拟结果可以看出，实验过程中试样内部发生的一些初始损伤，如微屈曲、纤维损伤和轻微分层，导致了曲线产生非线性现象，而破坏模式的变化主要是高温导致环氧树脂热软化所造成的。当老化实验温度低于树脂基体的Tg时，Z向纱对3DOWCs的剪切性能有一定的改善作用，但作用不明显；而当温度接近或者高于Tg时，其强化效果表现显著。此外，通过有限元模型分析可以看到，纤维增强先进树脂基复合材料在力学性能测试时，材料内部发生的复杂应力集中与破坏模式很难用常规手段直观表现处理，在高温老化条件下进行实验时更是如此，但采用有限元模型分析可以很清楚地知道材料内部的破坏模式和应力集中区域，且模拟结果与实验结果吻合良好，这也正是有限元模型的优势所在。

4.2.3.2　三维编织结构的均质模型与多层模型建立

先进树脂基复合材料在热氧老化条件下表面会形成一种薄薄的氧化层。为了从有限元角度了解基体氧化层局部性质差异对复合材料性能的影响，张曼（三维编织复合材料热氧老化效应及压缩性质降解机理）根据三维编织复合材料在180℃老化16天的宏观准静态压缩测试结果和微观纳米压痕测试结果，建立了均质模型和分层模型两种模型。

（1）模型定义：所谓均质和分层代表编织复合材料有限元模型所赋予的树脂基体属性。分层模型可呈现复合材料老化后由氧化反应导致的基体性质不均匀分布，而均质模型则引入树脂块老化后整体性质变化，是一种简化模型。

图4-22所示为两模型横截面示意图，其中白色小六边形区域代表编织纱分布。图4-22（a）均质模型中的基体区域统一为橙色，表示所有基体单元属性完全相同；图4-22（b）分层模型中不同颜色分别代表表面氧化层、第一过渡层、第二过渡层和未氧化中心。不同区域厚度和性质与纳米压痕测试结果保持一致。在此，不同区域树脂塑性性能差异不作考虑。从180℃老化16天环氧树脂准静态压缩响应中提取基体塑性性质，同时引入当前两个模型，针对“分层模型”，主要考虑热氧化所引起的基体局部性质差异，内部编织纱性质差异忽略不计。

图4-22　三维编织复合材料老化模型示意图

（2）模型参数定义：均质模型中基体弹性参数由环氧树脂准静态压缩应力—应变曲线线性段拟合得到，分层模型中基体弹性参数则根据纳米压痕所得模量变化率换算而来。两个模型基体取相同的塑性参数，由准静态压缩应力—应变曲线屈服段提取而得。针对180℃老化16天编织复合材料，两种细观有限元模型基体组分性质参数见表4-16。

表4-16　均质模型和分层模型树脂基体性质参数（180℃老化16天）

在低于200℃热空气中，碳纤维基本不会发生老化，其性质保持不变。编织纱被看作由碳纤维和环氧树脂共同构成的单向复合材料，其性质受树脂影响，老化后发生改变。针对180℃老化16天后复合材料有限元模型，编织纱弹塑性性质参数分别见表4-17、表4-18，其中R11代表纤维轴向。

表4-17　未老化及180℃老化16天编织纱弹性参数

表4-18　未老化及180℃老化16天编织纱塑性常数Rij

关于编织复合材料老化前纱线/基体界面性质参数，引用了Nishikawa和Phadnis等的研究。在180℃热氧环境中老化16天后，复合材料界面产生明显可见裂纹，部分纱线与基体脱黏，界面黏结性变差。但考虑到模型预置裂纹复杂性，采用简化方案，通过弱化有限元模型界面参数来表征编织复合材料老化后的界面损伤。具体界面参数见表4-19。

表4-19　初始及180℃老化16天后界面参数

（3）接触定义及加载模式：整个有限元模型的计算过程通过有限元分析软件静态求解器ABAQUS/Standard和LINUX系统操作平台实现。分析步类型采用Static General，压缩载荷分析步步长设置为50s。采用通用接触（General contact）定义压板和试样之间的接触，切向摩擦系数设为0.2。编织纱之间定义为自接触（Self contact），纱线和树脂基体界面用内聚力模型（Surface-based cohesive behavior）定义，其中纱线外表面设置为主面（Master surface），基体内表面设置为从面（Slave surface）。在准静态压缩过程中，将上下压板设置为刚体，压缩前后无变形，加载方式采用速度加载，在竖直方向给上压板施加一个大小恒定为2mm/min的速度，除上压板加载方向位移自由度外，对上下压板进行完全自由度约束。

（4）模拟实验结果。①应力—应变曲线。三维编织复合材料180℃老化16天后准静态面外压缩有限元模拟值与实验结果对比如图4-23所示。由于氧化区域基体单元模量较高，“分层模型”模拟所得应力—应变曲线要略高于“均质模型”，但两者差异很小，两条曲线基本重合且与实验结果吻合良好。这是因为编织复合材料老化过程中，氧化反应仅局限在材料表面一定厚度范围内，与试样整体尺寸相比，氧化层很薄，故其局部模量差异对编织复合材料整体压缩应力—应变曲线影响较小。由此可见，“均质模型”虽为简化模型，但仍可有效模拟三维编织复合材料热氧老化后准静态面外压缩应力—应变响应特征。

图4-23　三维编织复合材料准静态面外压缩应力—应变响应（180℃热氧老化16天）

②内部应力及损伤分布。图4-24和图4-25所示为准静态压缩加载后，“分层模型”和“均质模型”所得编织复合材料内部应力状态及界面损伤分布。通过云图对比可以发现，两个模型所得树脂基体、编织增强体内部应力及界面损伤分布基本一致，即使在表面氧化区域，应力大小和界面破坏程度也并未表现出明显差异，可见氧化层对编织复合材料受载过程中应力分布及界面损伤影响不大。

图4-24对比显示应力—应变曲线末端时刻，“分层模型”和“均质模型”模拟所得编织复合材料应力分布。为了更清晰呈现材料内部应力状态，将垂直于Y轴截取不同位置剖面云图，并将树脂基体和编织增强体应力分布分开显示。图4-24（a）所示为树脂基体应力云图。沿中心位置，基体应力分布基本左右对称，表明三维编织结构复合材料可看作准横观各向同性材料。基体中心部位和轴向棱边处出现应力集中，内部应力集中区呈现编织纱交错形态，体现出显著的结构效应。基体材料表面应力水平较低。图4-24（b）所示为纱线应力分布云图，由于编织结构准横观各向同性，纱线内部应力基本呈对称分布，此处仅取一半放大显示。编织增强体应力集中区多发生在纱线中段部位，两自由端应力相对较小。相比于内部直线段，编织纱表面屈曲部分更容易产生应力集中。图4-25是两个模型得到的界面损伤分布，标尺中“CSDMG”为损伤变量D，用灰度图表征损伤程度，颜色越深，界面损伤越严重。可以看到“分层模型”和“均质模型”应力及界面损伤分布规律基本一致。

图4-24　复合材料应力分布云图对比

图4-25　界面损伤分布对比

为进一步定量比较两个模型所得材料内部应力大小，分别沿内纱、面纱和角纱选择三条代表性路径，如图4-26（a）所示。提取沿所选路径基体和编织纱上对应位置节点应力，应力—位置关系见图4-26（b）～（d）。左列曲线图为两个模型所得到基体应力差异，除虚线框内局部位置外，两模型模拟得到的基体应力—位置曲线图基本重合。对比左侧纱线在复合材料内部空间分布，发现曲线图中应力存在差异的位置为复合材料表面氧化区域，在此处分层模型所得应力略高于均质模型，最大差异小于3%。图4-26（b）～（d）右列曲线图显示分层模型和均质模型所得编织纱应力分布差异。只有在角纱靠近复合材料氧化表层处两模型所得应力大小存在微小差异且最大差异小于2.8%[图4-26（d）右]。由此可见，无论是基体还是编织纱，分层模型和均质模型所得应力分布基本一致，局部区域微小应力差异不足以影响复合材料整体宏观力学性能。对在180℃热空气中老化16天三维编织复合材料而言，表面氧化层局部力学性质差异对老化后复合材料整体压缩性能影响很小。依此类推，在其他老化条件下（老化温度均低于180℃，最长老化时间为16天），氧化层影响也可忽略不计，均质模型作为一种简化模型，可有效获取编织复合材料老化后主要力学性质特征（应力—应变响应、应力及界面损伤分布等）。

图4-26　分层模型与均质模型应力分布定量对比