先进树脂基复合材料热氧老化寿命预测模型优化

先进树脂基复合材料长期暴露在热氧环境下会导致力学性能下降。由于弯曲强度可以综合反映基体和纤维/基体界面性能的变化，而且热氧老化对树脂基复合材料的影响主要是对其基体性能和纤维/基体界面性能的影响，因此将弯曲强度作为性能评定参数，利用热氧加速老化条件下的弯曲强度数据，可以预估先进树脂基复合材料在室温下的储存寿命。

要预估树脂基复合材料的储存寿命，首先必须建立老化性能评定参数B（根据应用条件选定）的数学模型，即B与温度T和时间t的关系（B—T—t三元数学模型）。由于用Arrhenius方程描述性能B随温度T的变化关系是高温加速老化的理论依据，所以凡是采用这一方法建立的预估模型的建模依据都是Arrhenius方程，而关键是怎样选取性能B随时间变化的数学模型。

4.1.2.1　先进树脂基复合材料热氧老化性能与老化时间的随机过程模型

先进树脂基复合材料的热氧老化包括纤维、基体、纤维/基体界面的老化。由于常用于增强先进树脂基复合材料性能的纤维的耐热氧老化性能较高，在低于200℃时不发生热氧老化，所以先进树脂基复合材料的老化主要包括基体树脂的物理化学变化以及由基体树脂老化引起的界面性能的退化。树脂的热氧老化过程包含有利部分（后固化）和不利部分（分子链断链和失重），所以老化后的性能是这两部分相互竞争的结果，当有利部分占主导地位时，材料的性能会上升，当不利部分占主导地位时，性能会下降。基体树脂的上述变化会引起界面性能的变化，这一过程导致的结果是不可预知的，是随机的，因此热氧老化导致整个先进树脂基复合材料性能退化过程十分复杂。然而，性能上升只会出现在固化不完全的先进树脂基复合材料上，而且只会在老化时间较短的情况下出现，随着老化时间的延长，先进树脂基复合材料的性能必定下降。对于完全固化和固化程度很高的先进树脂基复合材料基本不存在后固化，所以先进树脂基复合材料的性能随着老化时间的延长必定下降。为了简化建模过程，假设先进树脂基复合材料是完全固化的。

根据随机过程理论，对于一定环境下的先进树脂基复合材料，其性能下降量与它经历的时间有关。B（t）是某一环境中先进树脂基复合材料经历时间t时的性能值，虽然B（t）的一切可能取值是可以知道的，但它的确切值一般事先不知道，因此B（t）是与时间t有关的随机变量。设B0、Bi分别为t0=0、t≠0时的性能指标测试值。考虑到测试值一般不是整数，为了简化计算，乘以放大系数n，使其在测试精度内成为最小整数，即nB0、nBi。若先进树脂基复合材料经历时间t，具有性能B（t），老化结果必将使得B（t）≤B0，由于B（t）具有随机性，因此B（t）=Bi的概率为：

P（t, nBi）=p{B（t）=Bi, t}，nBi∈{0，1，2，……，nB0}

（4-12）

此外，设k＞0是先进树脂基复合材料的老化速率参数，o（∆t）是关于时间增量∆t的高阶无穷小量，即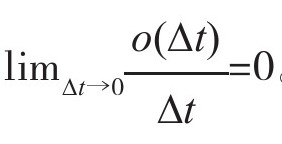。在时间区间（0，t）内，先进树脂基复合材料性能指标下降n（B0-Bi）个单位。如果时间增加∆t，那么在区间（t, t+∆t）内，先进树脂基复合材料性能下降一个单位，即nBi-1的概率是knBi∆t+o（∆t）。反之，性能下降小于一个单位的概率为1-knBi∆t+o（∆t）。由于老化的缓慢性，故∆t很小时，其性能下降大于一个单位的概率显然是o（∆t）。于是先进树脂基复合材料在t+∆t时刻性能Bi≥0的概率为：

P（t+∆t, nBi）=（1-knBi∆t）P（t, nBi）+k（nBi+1）∆tP（t, nBi+1）+o（∆t）

（4-13）

整理式（4-13），并取∆t→0时的极限，导出下列微分方程：

由于在t=0时，先进树脂基复合材料的性能指标由测试获得，故nBi=nB0的概率等于1，而nBi≠nB0的概率等于0。于是，得到微分方程式（4-14）的初始条件：

因此，式（4-14）应在初始条件式（4-15）下求解。

当nB1=nB0时，代入式（4-14），得

故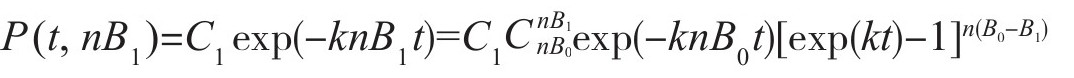

从初始条件P（t, nB1）=1，nB1=nB0，可知C1=1。

当nB2=nB0-1时，代入式（4-14），得：

因此

P（t, nB2）=exp[-k（nB0-1）t]（∫knB0exp（-knB0t）exp（∫k（nB0-1）dt）dt+C2）（4-18）

从初始条件P（0，nB2）=0，nB2≠nB0，可知C2=nB0。将nB0代入上式，并整理得：

于是，得到递推关系式：

根据数学归纳法，得到关于先进树脂基复合材料的性能与时间的概率分布函数为：

当nBi确定后，可以证明式（4-21）存在关于时间的极大值。

现在由式（4-21）求在时间t时，先进树脂基复合材料性能指标平均值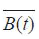的预测公式。

由于：

令

z=exp（kt）-1

（4-23）

代入上式，得：

将z=exp（kt）-1代入上式，整理得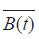，的预测公式为：

此外，设先进树脂基复合材料性能测试的试样数量为m；B1，B2，……，Bm分别m为个试样经老化时间t后的测试值。根据极大似然估计法（MLE），得到参数k的对数似然函数为：

整理式（4-26）可得到下列微分方程：

解似然方程得老化速率参数为：

式（4-28）表明由先进树脂基复合材料本身性质及使用环境所决定，与n无关，把式（4-28）代入式（4-25），得到：

式（4-29）从理论上说明，预测性能平均值和实测结果平均值相等。由此可知，任意t的预测值可用实测值验证。反之，式（4-25）确实可用来预测先进树脂基复合材料的性能。

4.1.2.2　先进树脂基复合材料热氧老化随机过程模型的验证与讨论

（1）先进树脂基复合材料热氧老化随机过程模型

公式（4-25）为指数模型（非线性），对非线性函数的处理办法通常是通过变换将其转化为线性函数，然后对线性函数进行检验。对式（4-25）两边取自然对数将其转化为下列线性模型：

令y=ln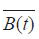；a=lnB0。上式变为：

y=a-kt

（4-31）

以如表4-1所示的层合试样和三维编织试样在不同老化温度下老化不同时间后测得的弯曲强度值来验证理论模型的正确性。

表4-1　层合试样和三维编织试样在不同老化温度下老化不同时间后测得的弯曲强度值

图4-1为用式（4-31）对三维四向编织碳/环氧复合材料在80℃、100℃、120℃和140℃下老化不同时间后的所有弯曲强度测试值进行拟合的结果。从图4-1（a）～（d）可以直观地看到四个温度下的实验值并没有均匀地分散在拟合直线两边，尤其是当t=0（即未老化的试样）时，图4-1（b）、（c）和（d）图中的拟合直线都偏离了实验值，而且都小于实验值。这与实际情况不相符，因为未老化的试样不可能出现性能的下降。从四个加速老化温度下的拟合直线调整后的R2（相关系数的平方，当R2=1时意味着预测值和实验值完全匹配）可以看到，所有的R2≤0.90，显然这一拟合结果不够理想。因此，需要对上述四个温度下的回归方程进行诊断，找出其“病症”所在。

以残差为纵轴而以拟合值或者其他量为横轴的图称为残差图。图4-2（a）～（d）为分别与图4-1（a）～（d）对应的回归直线的标准化残差图，也称为学生化残差图。从图4-2可以看到，四个温度下的残差并没有均匀地分布在中心线的两侧，而是呈现出一种中间向下凹陷的“症状”，这种“疾病”表明回归函数可能是非线性的，或者漏掉了一个或多个重要的回归自变量。因为先进树脂基复合材料在特定温度下的强度值只与老化时间有关，所以上述“病症”应该是弯曲强度的自然对数和老时间之间不是线性关系导致的，也即存在非线性关系。

针对自变量和因变量之间为非线性的问题，有很多解决办法，其中Box—Cox变换是从综合角度考虑提出的一种“治疗方案”，在实际应用中效果比较好。因此，采用Box—Cox变换对式（4-31）进行“治疗”，经过Box—Cox变化后得到式（4-32）：

图4-1　用式（4-31）对三维四向编织碳/环氧复合材料在80℃、100℃、120℃和140℃下老化不同时间后的弯曲强度测试值进行拟合的结果

y=a-ktλ

（4-32）

式中：λ为一个待定变换参数。对不同的λ，所做的变换自然就不同，所以这是一个变换族。Box—Cox变换就是通过对参数的适当选择，达到对原来数据的“综合治理”，使其满足正态线性回归模型的所有假设条件。

采用逐次逼近法可以估计参数λ。求解准则是令的估计精确到小数点后两位数时式（4-33）的值最小。

式中：yij为在某一温度下第个老化时间点，第j个试样的实验值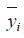；为上述老化温度下第i个老化时间点的预测值。

图4-2　与图4-1对应的回归直线的学生化残差图

在λ为某一尝试值时，令式（4-32）中的w=tλ。式（4-20）可以变换成如下的直线形式：

y=a-kw

（4-34）

按最小二乘法估计a和k。

在求得a后可以反推求得B0，于是：

在计算机上利用SPSS软件根据计算准则I对λ进行尝试计算，计算得到λ的最佳值都为0.56。

图4-3为λ=0.56，并且按照式（4-34）将三维四向编织碳/环氧复合材料不同老化温度下的弯曲强度值拟合后的结果。从图4-3可以看到四个老化温度下的实验值都均匀分布在拟合直线的两边，而且R2都大于0.90。此外，从图4-4可以看到，每个温度下的残差都均匀分布在中心线的两侧。这说明，经过Box—Cox变换的式（4-32）能够很好地刻画三维四向编织碳/环氧复合材料弯曲强度和老化时间的关系。

图4-3　用式（4-32）对三维四向编织碳/环氧复合材料在80℃、100℃、120℃和140℃下老化不同时间后的弯曲强度测试值进行拟合的结果

将式（4-32）还原为某一温度下的性能预测模型，如式（4-38）所示。式（4-38）就变为式（4-25）的形式，也即随机过程推出的性能预测模型式（4-25）是式（4-38）的一种特例，也可以说式（4-38）是一种更大类的随机过程模型，这里我们将其称作为先进树脂基复合材料热氧老化的“改进型随机过程模型”。

图4-4　与图4-3对应的回归直线的标准化残差图

在建立“改进型随机过程模型”时没有对先进树脂基复合材料的增强体结构加以限制，所以“改进型随机过程模型”应该也适用于任何增强体结构增强的树脂复合材料性能与寿命预测。利用上述拟合三维四向编织碳/环氧复合材料数据的方法来处理层合平纹碳布/环氧复合材料各老化温度下的数据。表4-2是利用式（4-35）～式（4-37）进行计算而得到的“改进型随机过程模型”中的参数值。

表4-2　三维四向编织碳/环氧复合材料和层合平纹碳布/环氧复合材料各温度下的老化速率常数和强度初始值

用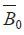代替式（4-38）中的B0，并用Origin 8.0软件进行作图，结果如图4-5所示。具体作图过程为：首先，在Origin8.0软件中自定义“改进型随机过程模型”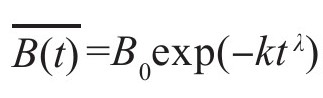；其次，将某一温度下获得的所有实验值画成散点图；最后选择非线性拟合，将求得的每个温度下的参数k, B0以及λ的值作为初始值，并将其固定，然后选择Fit按钮作图。

图4-5　用式（4-38）对层合平纹碳布/环氧复合材料在80℃、100℃、120℃和140℃下老化不同时间后的弯曲强度测试值进行拟合的结果(www.xing528.com)

从图4-5可以看到，实验数据很好地分布在拟合曲线的两侧，这说明“改进型随机过程模型”也适合层合平纹碳布/环氧复合材料性能与寿命的预测。将三维四向编织碳/环氧复合材料各温度下的弯曲强度也采用与层合平纹碳布/环氧复合材料相同的方法在Origin 8.0中进行作图，结果如图4-6所示。

图4-6　用式（4-38）对三维四向编织碳/环氧复合材料在80℃、100℃、120℃和140℃下老化不同时间后的弯曲强度测试值进行拟合的结果

（2）先进树脂基复合材料热氧老化随机过程模型验证。从“改进随机过程模型”建立先进树脂基复合材料的老化模型时无须考虑增强纤维的种类和增强体结构，只需知道材料在特定环境下的老化参数，而老化参数可以通过实验获得，因此，可以用来预测不同增强结构的先进树脂基复合材料在热氧老化前后的剩余强度，之后与实验室进行对比，以验证“改进随机过程模型”建立先进树脂基复合材料的老化模型的可行性。

表4-3为三向正交复合材料在200℃条件下进行了不同时间的老化后的弯曲强度数据。采用式（4-31）对老化120天内的数据进行线性拟合，根据I准则不断逼近求得λ，得到的具体数据如表4-4所示。首先，将实验得到的弯曲强度数据输入Origin 8.5软件中绘制散点图；其次，在软件中采用式（4-38）对数据进行非线性拟合；最后，将各时间段计算得到的参数值k，λ和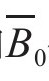作为初始值输入，点击Fit拟合曲线，结果如图4-7所示。

表4-3　200℃下三向正交复合材料老化前后的弯曲强度值

表4-4　外推曲线得到的相关参数

用式（4-31）对200℃老化120天的试验数据进行拟合后的相关系数R2为0.97434。相关系数大于0.95，因此认为实验值和预测值有很强的相关性。所以，该“改进随机过程模型”可以预测一定条件下先进树脂基复合材料的性能值。因此，可以得到，在200℃下老化时间和弯曲强度预测模型为：

图4-7　用式（4-32）对三向正交复合材料在200℃老化120天内的弯曲强度实验值拟合的结果

B（t）=801.68exp（-0.01619t0.85003）

（4-39）

用上式对200℃老化180天的弯曲强度进行了预测，并与实验值进行了对比，具体数据如表4-5所示。预测误差的计算如式（4-40）所示：

可以看到，预测误差小于10%，说明了该模型具有一定的可靠性。

表4-5　用随机过程理论计算的预测值与实验值的对比

此外，使用“改进随机过程模型”来预测面内准各向同性编织复合材料在200℃下老化180天的剩余弯曲强度，并与实验值进行对比。表4-6为三向正交复合材料在200℃条件下进行了不同时间的老化后的弯曲强度数据。采用式（4-31）对编织复合材料在200℃条件下老化120天内的弯曲强度进行线性拟合，用逐次逼近法求得λ，得到的具体数据如表4-7所示。

表4-6　面内准各向同性编织复合材料和层合复合材料在不同老化温度下老化不同时间后测得的弯曲强度值

表4-7　外推曲线得到的相关参数

然后先以老化120天内的弯曲强度为纵坐标，老化时间为横坐标，使用Origin8.5软件绘制散点图。之后将式（4-38）代入λ和B0的值后进行非线性拟合，结果如图4-8所示。拟合后的相关系数R2为0.9596，实验值几乎都均匀分布在拟合曲线两侧，说明此拟合结果较为理想。因此，面内准各向同性编织复合材料在200℃条件下老化120天的强度预测模型即为：

B（t）=361.96exp（-0.01402t0.79）

（4-41）

之后用式（4-41）预测面内准各向同性编织复合材料在200℃条件下老化180天后的弯曲强度进行预测，并与实验值进行了对比。具体数值如表4-8所示，拟合曲线如图4-9所示。可以看到预测误差为3.26%，且实验值均匀分布在拟合曲线两侧，说明使用“改进型随机过程模型”进行树脂基复合材料老化后的强度预测是一种可行的方法。

图4-8　用式（4-41）对编织复合材料在200℃条件下老化120天内的弯曲强度测试值进行拟合的结果

表4-8　用改进型随机过程理论计算的预测值与实验值的对比

图4-9　用式（4-41）对编织复合材料在200℃条件下老化不同时间后的弯曲强度测试值进行拟合的结果

此外，使用“改进随机过程模型”来拟合碳纤维/双马树脂界面在200℃下老化180天的剩余强度（由横向纤维束拉伸实验测得）。表4-9为横向纤维束拉伸试样在200℃下老化不同时间后测得的碳纤维/双马树脂界面强度值。采用式（4-31）对200℃条件下老化180天内的碳纤维/双马树脂界面强度进行线性拟合，即以老化180天内的界面强度为纵坐标，老化时间为横坐标，使用Origin8.5软件绘制散点图。之后进行非线性拟合，结果如图4-10所示。拟合后的相关系数R2为0.90，实验值几乎都均匀分布在拟合曲线两侧，说明此拟合结果较为理想。这代表着使用“改进型随机过程模型”进行纤维/树脂界面老化后的强度预测是一种可行的方法。

表4-9　横向纤维束拉伸试样在200℃下老化不同时间后测得的碳纤维/双马树脂界面强度值

图4-10　用“改进型随机过程模型”对碳纤维/双马树脂界面在200℃条件下老化不同时间后的强度测试值进行拟合的结果

4.1.2.3　先进树脂基复合材料老化速率常数与老化温度的类Arrhenius模型

“改进型随机过程模型”是在某一确定温度下，先进树脂基复合材料性能评定参数B与老化时间t的二元统计模型，然而要想得到先进树脂基复合材料室温下的储存寿命，也即将高温加速老化下得出的规律外推到自然状态下，就必须建立老化速率常数与老化温度T的（k—T）二元模型。Arrhenius方程是描述化学反应速率常数与温度T之间定量关系的数学表达式，它是高温加速老化的理论依据。因为聚合物的热氧老化速率常数与温度之间的关系符合Arrhenius方程，而热氧老化对先进树脂基复合材料性能的影响主要是通过对基体聚合物的老化实现的，所以先进树脂基复合材料的老化速率常数与温度之间也应该符合类似Arrhenius的方程。

先进树脂基复合材料热氧加速老化速率与温度的关系服从如下的类Arrhenius方程形式：

式中：A, D为常数；T为热力学温度，k为老化速率常数。

对式（4-42）两边取对数得式（4-43）：

令W=lnk, E=lnA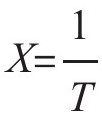，，上式可以改写为：

W=E-DX

（4-44）

用各温度下的老化速率常数k值（表4-1）对式（4-44）进行线性相关性检验（γ检验）。先查相关系数表，以置信概率为99%，自由度=-2查得的γb值与计算求得的γ值比较。如果|γ|＞γb，则X与W的线性关系成立；如果|γ|＜γb，则X与Y的线性关系不成立，证明选择的老化数学模型不合适。

相关系数γ计算如下：

w的标准偏差为：

式中：

则W的置信区间的上限为：W=E-DX+τSw，式中τ可以通过自由度（df=p-2）和显著性水平为0.05时的单侧界限表查出，为2.920。

由最小二乘法和式（4-45）、式（4-46）分别计算得到E, D，γ和Sw和的值如表4-10所示。

表4-10　三维四向编织碳/环氧复合材料和层合平纹碳布/环氧复合材料线性相关性统计分析的参数值

相关系数表中显著水平为0.01，自由度为2（df=p-2）时γb=0.990。表4-10中层合平纹碳布/环氧复合材料和三维四向编织碳/环氧复合材料的绝对值都大于0.990，说明两种复合材料的老化速率常数和老化温度都满足式（4-44）的线性关系，也即两种复合材料的老化速率常数和老化温度之间的关系服从式（4-42）的类Arrhenius方程。图4-11和图4-12分别为层合平纹碳布/环氧复合材料和三维四向编织碳/环氧复合材料老化速率与老化温度的拟合直线。从图中可以看到实验值很好地落在了拟合直线上或者均匀分布在拟合直线的两边。

图4-11　层合平纹碳布/环氧复合材料老化速率与老化温度之间的关系

图4-12　三维四向编织碳/环氧复合材料老化速率与老化温度之间的关系

层合平纹碳布/环氧复合材料的置信区间的上限为：

lnk=2.0859-2988.15/T+2.290×0.0250

（4-48）

三维四向编织碳/环氧复合材料的置信区间的上限为：

lnk=2.0604-3087.71/T+2.290×0.0534

（4-49）

4.1.2.4　三维四向编织碳/环氧复合材料和层合平纹碳布/环氧复合材料热氧老化下的储存寿命

通过4.2.2和4.2.3的分析可知，先进树脂基复合材料在热氧老化下的性能预测模型（B—t—T）为下式：

将上式t反解出来即可获得CFPMCs的寿命预测模型：

因为保留率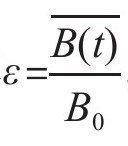，所以上式可以改写为：

将之前求得的三维四向编织碳/环氧复合材料和层合平纹碳布/环氧复合材料的参数带入式（4-52）可得到三维四向编织碳/环氧复合材料和层合平纹碳布/环氧复合材料的寿命预测模型。

三维四向编织碳/环氧复合材料的寿命预测模型为：

层合平纹碳布/环氧复合材料寿命预测的模型为：

若将老化速率常数的上限值带入式（4-49）中，可得到两种复合材料寿命下限的预测模型。

三维四向编织碳/环氧复合材料寿命下限的预测模型为：

层合平纹碳布/环氧复合材料寿命下限的预测模型为：

此时可以用式（4-53）～式（4-56）去外推计算三维四向编织碳/环氧复合材料和层合平纹碳布/环氧复合材料的室温储存寿命。在做室温储存寿命实验时需要做以下基本假设：

（1）在实验温度至常温区间内先进树脂基复合材料的老化机理相同，储存过程中所选定的老化性能评定参数值的变化速率只受温度影响，与其他因素无关。

（2）老化过程中材料的老化速率与温度的关系服从类Arrhenius方程的形式。

在储存条件下T储存=298K，根据先进树脂基复合材料的实际使用要求，若以弯曲强度保留率0.7作为先进树脂基复合材料储存时的性能临界值，按照式（4-53）～式（4-56）可计算得到三维四向编织碳/环氧复合材料和层合平纹碳布/环氧复合材料的室温储存寿命，如表4-11所示。

表4-11　三维四向编织碳/环氧复合材料和层合平纹碳布/环氧复合材料的室温储存寿命

从表4-11可以看到三维四向编织碳/环氧复合材料的平均储存寿命和储存寿命下限分别比层合平纹碳布/环氧复合材料约长17年和10年。这一结果与在相同的高温加速老化下三维四向编织碳/环氧复合材料的弯曲强度保留率总是大于层合平纹碳布/环氧复合材料的结果相一致，说明用三维四向编织预制件增强的先进树脂基复合材料具有更强的耐热氧稳定性。