算法和程序流程框图的设计优化方案

1.算法的设计

（1）本实例要求铣削一个1/4长半轴为29.9mm、短半轴为18.9mm的椭圆面轮廓，该实例和实例8-2在编程的算法和思路上有相似之处。

（2）椭圆面可以看成是由无数条直线组成的图形集合，组成图形集合的直线之间满足椭圆方程函数关系，可以根据加工图形和刀具之间关系建立图8-28所示的数学模型，并可以采用数学表达式表示刀位点之间的关系。

（3）根据图8-28所示建立的数学模型，设置#100号变量控制椭圆的角度θ；由图8-27零件图可知，椭圆角度的变化范围为180°～270°，可见#100号变量的初始值既可以是180°，也可以是270°（这点在后面会进行详细的分析）。

设置#101号变量控制椭圆上任意一点对应长半轴的值，设置#102号变量控制椭圆任意一点对应短半轴的值。

图8-28 铣削椭圆面数学模型示意图

（4）椭圆解析方程可以转换为椭圆参数方程，如其解析方程为X²/A²+Z²/B²=1，则以θ为变量的参数方程为X=A∗COS[θ]、Z=B∗SIN[θ]。

在数控加工实际编程过程中，需要根据加工零件图建立数学模型，进一步去判断采用椭圆解析方程还是椭圆参数方程。

（5）在本实例中，根据加工零件图以及建立的数学模型，选择椭圆参数方程要比椭圆解析方程方便。

根据椭圆参数方程可知，在图8-28所示的数学模型中，可以建立表达式：#101=[椭圆长半轴的值]∗SIN[#100]、#102=[椭圆短半轴的值]∗COS[#100]。

（6）#100号变量初始值的选择与加工方式有关。在前面的章节，已经阐述过此类零件加工的进刀方式：“自下而上”铣削模式和“自上而下”铣削模式（在此仅叙述进刀类型），并进行了详细分析。

在本实例中，采用“自下而上”的进刀铣削模式，#100号变量赋初始值为270°；若采用“自上而下”的进刀铣削模式，#100号变量赋初始值为180°。

（7）在本实例中，椭圆的角度终止值作为循环结束的判断条件，显然采用不同的进刀铣削模式，循环结束的条件不相同：采用“自下而上”的进刀铣削模式判断语句用IF[#100 GE 180]GOTO n控制整个铣削的循环过程；采用“自上而下”的进刀铣削模式判断语句用IF[#100 LE 270]GOTO n控制整个铣削的循环过程。

2.算法流程框图设计

根据以上算法设计和分析，规划“双向往复循环”铣削模式的铣削刀路轨迹如图8-29所示，“单向往复循环”铣削模式的铣削刀路轨迹如图8-30所示（中间的刀路轨迹不在图中表示），“单向往复循环”铣削模式的程序设计流程框图如图8-31所示。

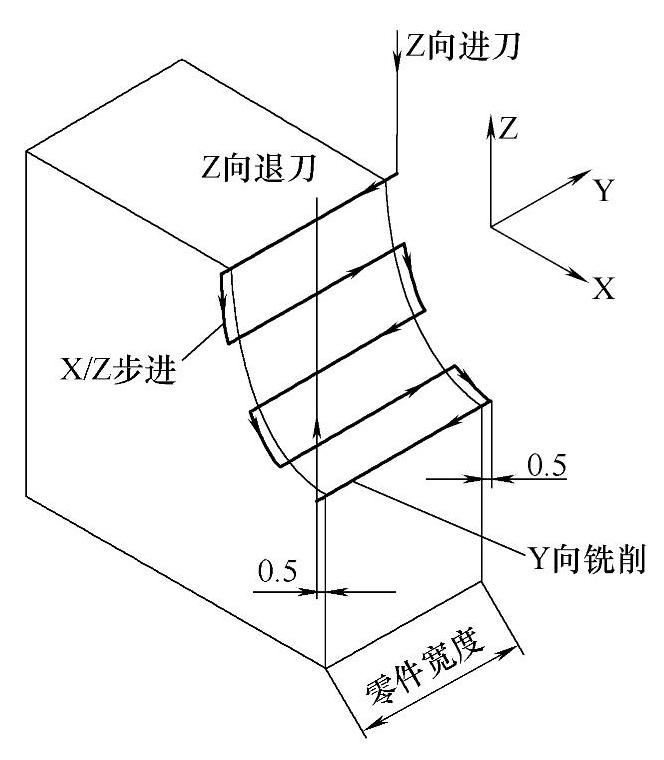
图8-29 “双向往复循环”刀路轨迹示意图

图8-30“单向往复循环”刀路轨迹示意图(www.xing528.com)

1—第1条刀路轨迹 2—中间刀路轨迹 3—最终刀路轨迹

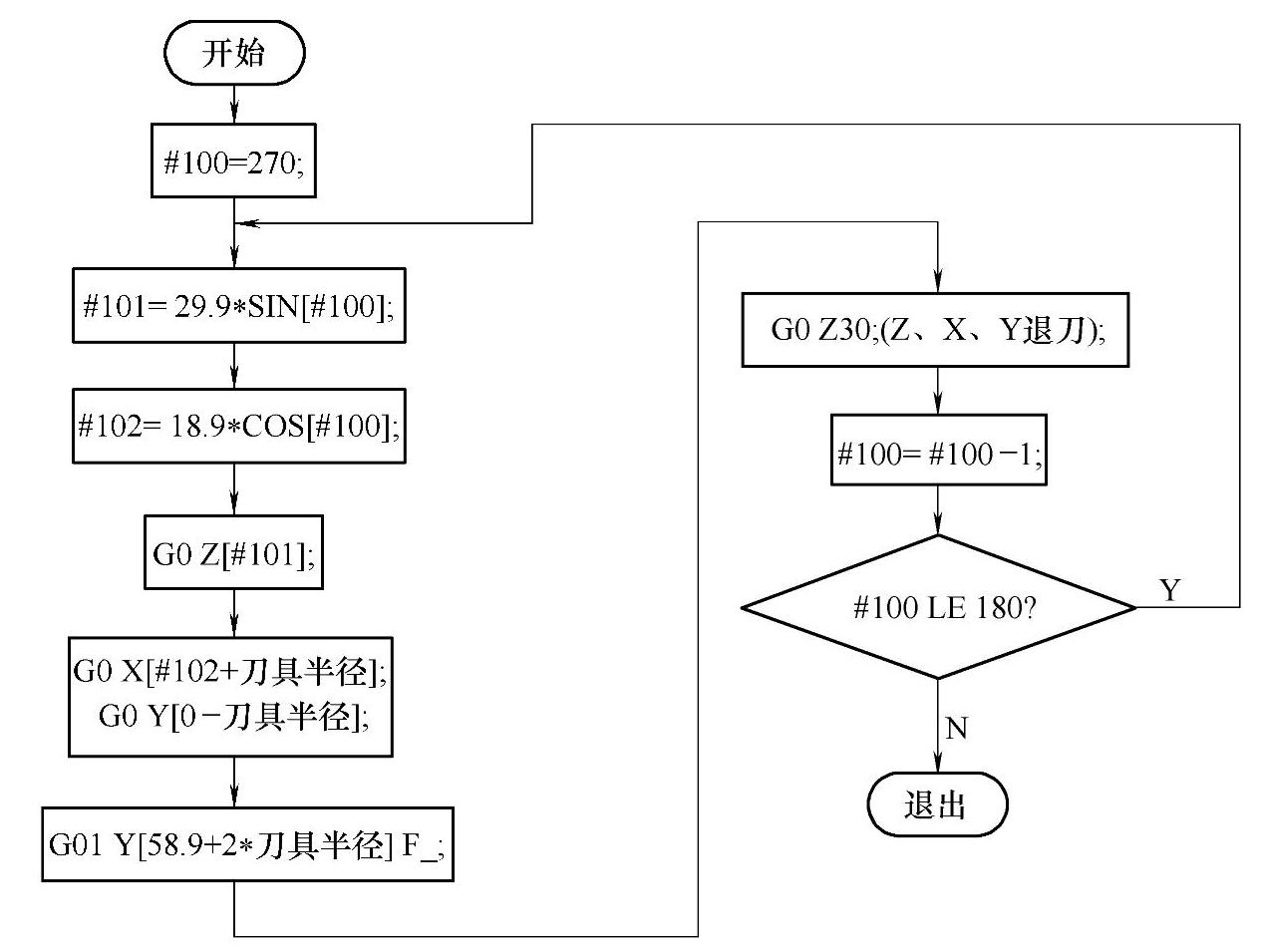
图8-31 “单向往复循环”铣削模式程序设计流程框图

从以上“双向往复循环”铣削模式刀路轨迹图和“单向往复循环”铣削模式刀路轨迹图比较可知，它们的本质区别在于：双向式刀路铣削一条直线后，X向再次进给一次步距，重新计算和#100号变量对应的#101、#102号变量的值，再次进行直线插补铣削，如此往复完成1/4椭圆面的铣削加工；单向式刀路铣削一条直线后，X、Z、Y轴都抬刀至直线铣削的起点位置（先Z轴抬刀至安全平面，后X、Y轴移动），然后X向再次进给一个步距的值，再铣削一条直线，如此往复完成1/4椭圆面的铣削加工。

3.根据算法以及流程框图编写加工的宏程序代码

程序1：采用“双向往复循环”铣削模式铣削椭圆面的宏程序代码

实例8-4 程序1编程要点提示：

（1）程序O8008采用“双向往复循环”铣削模式进行铣削椭圆面的宏程序代码，该程序编程思路：通过建立数学模型计算刀位点的坐标值，采用Y0向+Y方向进行直线插补的铣削方式，通过循环控制语句IF[#100GE180]GOTO10实现整个椭圆面的铣削过程。

（2）实例8-2和实例8-3的加工型面满足曲线的一次方程，需要计算其中一个坐标轴的值即可；实例8-4的加工型面满足曲线的二次方程，需要计算刀位点X和Z两个坐标轴的值。

（3）实例8-4采用的铣削方式与#100号变量赋初始值以及条件判断语句有密切的关系。从图8-27可知，铣削椭圆面的角度变化范围为180°～270°，采用“自下而上”的进刀铣削方式，角度初始值应为#100=270；采用“自上而下”进刀铣削方式，角度初始值应为#100=180，在编程中应根据实际进刀方式的需要确定该角度的初始值。

程序2：采用“单向往复循环”铣削模式铣削椭圆面的宏程序代码

实例8-4 程序2编程要点提示：

（1）程序O8009采用“单向往复循环”铣削模式和“自上而下”加工方法进行铣削椭圆面的宏程序代码，该程序编程思路：根据数学模型计算刀位点的坐标值，然后采用Y0向+Y方向直线插补的铣削方式，通过循环控制语句IF[#100 LE 270]GOTO 10实现整个椭圆面的铣削过程。

（2）程序O8009与O8008的区别在于：程序O8009采用“单向往复循环”铣削模式和“自上而下”加工方法铣削椭圆面的宏程序代码；O8008采用“双向往复循环”铣削模式和“自下而上”加工方法铣削椭圆面的宏程序代码。

（3）程序O8009适用于已经去除大量余量的精加工，不适用于零件的粗加工。其他编程要点提示请参考程序O8008编程要点提示部分的内容。