1.算法的设计
(1)该实例是斜椭圆弧轮廓的加工,轮廓所处的位置和实例5-1有相同之处,而区别在于:本实例椭圆的中心线(也称之为中心对称轴)与X/Y轴方向不重合。
该实例也可以采用椭圆解析方程、参数方程来编制加工程序代码,其变量的选用方法、算法的设计思路参考实例5-1铣削整椭圆轮廓的宏程序应用实例。
(2)本实例中,椭圆的中心线与X轴的正方向呈15°的夹角,在整个程序中清楚表达该角度为编程的关键,现有以下两种方法解决:
1)FANUC系统中,采用旋转坐标系G68(G69)编程是解决旋转类零件最有效的指令。只要指定旋转中心和旋转角度,就可以按照零件的中心线作为X/Y轴进行编程。
例如:本实例中椭圆的旋转中心点为编程原点,旋转角度为15°,按照G68角度正负指定的原则,该零件的旋转角度为正15°。
关于旋转坐标系G68(G69)编程指令以及更为详细的应用说明,可以参考相关数控系统的使用手册。
2)采用矩阵旋转的原理进行编程
该实例可以看做:倾斜椭圆是将椭圆绕其中心线旋转某个角度而成(通常取逆时针为正方向),可以采用椭圆解析方程或参数方程,通过数学表达式来表示旋转后椭圆上所有点的坐标值,再利用G01直线拟合的方式铣削斜椭圆整个轮廓。
把椭圆上所有点的集合看做一个矩阵形式,而斜椭圆上所有的点可以看做由矩阵旋转而成的另一个矩阵,公式为:

其中β为旋转角度,[X′,Y′]是旋转之前的坐标值,[X,Y]是旋转之后的坐标值,由该式可以得出:X=X′∗cosβ-Y′∗sinβ和Y=X′∗sinβ+Y′∗cosβ。
2.刀具轨迹图以及程序流程框图的设计
根据以上算法设计和分析,规划铣削倾斜椭圆轮廓的刀路轨迹如图5-14所示,采用旋转坐标系方法的程序流程框图如图5-15所示,而采用矩阵旋转原理的程序流程框图如图5-16所示。
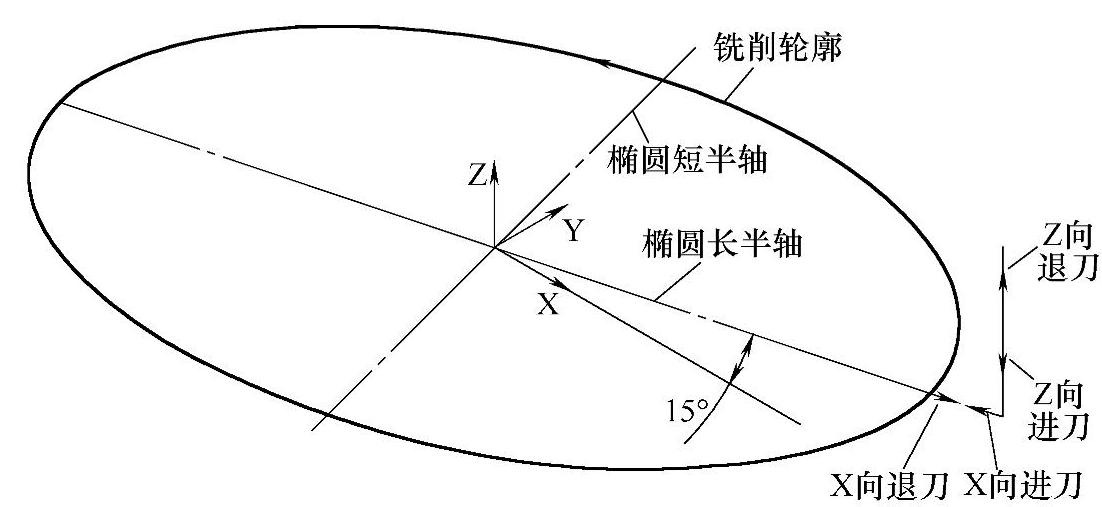
图5-14 倾斜椭圆轮廓的刀路轨迹示意图

图5-15 采用旋转坐标系程序流程框图
 (https://www.xing528.com)
(https://www.xing528.com)
图5-16 矩阵旋转原理铣削椭圆轮廓程序流程框图
3.根据算法以及流程框图编写加工的宏程序代码
程序1:采用旋转坐标系编写的宏程序代码


实例5-3 程序1编程要点提示:
(1)该程序是采用FANUC系统提供的编程指令G68(G69)旋转坐标系来编写的宏程序代码。旋转坐标系G69(G68)编程指令,在实例2-4铣削圆周槽的宏程序应用实例中进行过说明,在此不再赘述。
(2)对旋转坐标系的旋转角度R值设置一个变量,以适合不同旋转角度的编程要求。
(3)关于控制铣削椭圆循环过程的方法在实例5-1和5-2中进行了较为详细地分析,在此也不再赘述。
程序2:采用矩阵旋转原理编写的宏程序代码


实例5-3 程序2编程要点提示:
(1)程序O5013采用矩阵旋转公式计算出旋转椭圆上各点的坐标值,再利用直线插补功能(G01)编写宏程序代码,通过数学表达式表示出椭圆旋转前后各点的对应关系。
(2)计算倾斜椭圆轮廓上各点的坐标值步骤:
1)计算未旋转之前椭圆上任意一点的坐标值,参见程序中的语句:#101=[30+#106]∗COS[#100]、#102=[20+#106]∗SIN[#100]。
2)将旋转角度代入旋转坐标公式,直接套用旋转坐标公式,参见程序中的语句:#103=#101∗COS[15]-#102∗SIN[15]和#104=#101∗SIN[15]+#102∗COS[15]。
(3)关于整个椭圆的循环过程、Z向分层铣削椭圆的变量设置以及循环的控制过程,参见实例5-1编程算法以及编程要点提示。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




