设计算法流程框图及程序流程

1.算法的设计

（1）本实例铣削均匀分布在圆周上的三个腰形凹槽，凹槽形状、大小一致，但各自的起点和终点的位置不同，可以将一个凹槽加工的程序编写成一个独立的子程序，在主程序中调用该子程序；也可采用G68、G69旋转坐标系进行圆周分布凹槽的加工。

（2）铣削一个凹槽型腔的思考。从图样分析可知：进行凹槽加工需要知道凹槽型腔起点和终点坐标位置，而确定凹槽型腔起点和终点坐标位置，可以有以下方法：

1）采用极坐标系G16、G15，旋转坐标系G68、G69来编写宏程序代码。

2）建立如图3-30所示的数学模型，利用三角函数关系，计算出凹槽型腔的起点和终点坐标值，该图中的#101～#108号变量的值，可以通过三角函数公式进行计算。

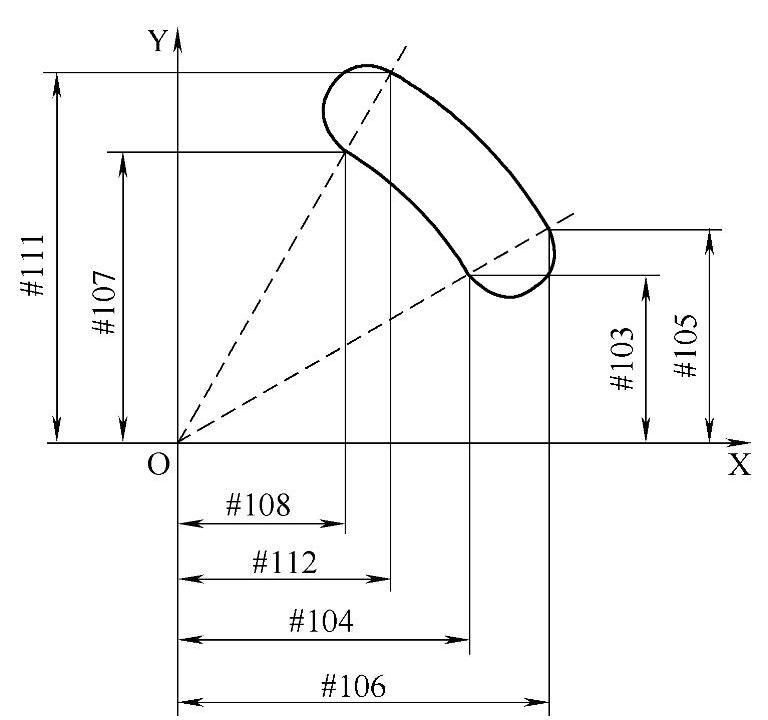
图3-30 腰形凹槽加工的数学模型示意图

（3）在深度方向采用分层铣削的方式，每层铣削深度为2mm，可以采用子程序嵌套的方式，也可以设置#115号变量来控制深度铣削的变化。

2.程序流程框图设计

根据以上算法设计分析，规划的精加工刀路轨迹如图3-31所示，加工流程框图的设计如图3-32所示。

图3-31 精加工刀路图

图3-32 流程框图的设计

3.根据算法以及流程框图编写加工的宏程序代码

程序1：利用三角函数公式计算腰形槽起点、终点位置的精加工宏程序代码

(www.xing528.com)

实例3-4 程序1编程要点提示：

（1）本程序采用最基本的方法———三角函数关系来计算出圆弧各点的坐标值。

（2）本程序采用刀心编程。采用三角函数关系计算各点的坐标值，需要考虑刀具半径，如程序中语句#113=[150-#101]∗SIN[#100]、#107=[110+#101]∗SIN[#100]；在建立数学模型的三角形时，需要考虑斜边值是加上刀具半径的值，还是减去刀具半径的值。

（3）由于三个圆弧凹槽均匀分布在圆周轮廓上，相邻两个凹槽之间角度间隔为120°，参见程序中语句：#100=#100+120、IF[#100LE270]GOTO20，它们控制了三个凹槽的循环加工。注意：循环结束条件是小于或等于270°而不是360°。

（4）程序是铣削好一个凹槽后，抬刀一定高度后，再进行下一个凹槽的加工，按深度优先的方法来铣削凹槽；也可以铣削好凹槽的一层以后，抬刀一定高度后，再进行另一个凹槽的加工，按层优先的方法进行铣削加工。

（5）加工完一个凹槽后，要先将Z轴抬刀至安全平面，见程序中G90G0Z20的语句。

程序2：利用极坐标系G16、G15和旋转坐标系G68、G69指令编写宏程序代码

实例3-4 程序2编程要点提示：

（1）本程序综合应用了刀具半径补偿、极坐标系、旋转坐标系、镜像以及比例缩放等数控铣手工编程中的高级编程指令。在宏程序编程的应用中，结合这些高级编程指令可以简化程序，使程序变得更具逻辑性和可读性。

（2）关于半径补偿、极坐标系、旋转坐标系等指令的综合应用说明：

半径补偿、极坐标系、旋转坐标系的应用如果出现在同一个程序中，使用的原则为“最先建立最后取消”或“最后采用最先取消”。下面结合程序中的语句具体分析：

旋转坐标系指令G68是最先建立的，参见程序中语句G68 X0 Y0 R[#100]，在程序的最后才采用G69指令来取消。

在手工编程尤其程序量较大或比较复杂的程序中，如需使用一些成对出现的指令如：G41 G42和G40、G68和G69、G15和G16等指令，在使用后一定要记得采用相对应的指令来取消，否则机床会执行不正确动作。

（3）关于G00 Z[#115+1]、#115=#115-2、G01 Z[#115]F100语句的说明：

刀具半径补偿在工件表面外建立，每铣削一层后，将Z轴抬刀到工件表面外，取消刀具半径补偿功能，参见程序中G90 G00 Z10语句。同时，为了减少空切时间，提高效率，要采用较快速度到达上层铣削的深度，参见程序中的语句G01 Z[#115]F500，然后再采用较低速度进给到下一层的铣削深度，参见程序中的语句G01 Z[#115]F100。