算法与程序流程框图的设计

1.算法的设计

（1）为了简化编程，从圆的+X向（即X50、Y0处为起始点），然后顺（逆）时针铣削整个圆弧轮廓。

（2）考虑采用刀具半径补偿来减少程序的计算量；考虑刀具切入的安全，可以采用1/4圆弧过渡进刀方式切入零件，退刀也采用1/4圆弧过渡退出零件。

（3）可以采用传统的G03或G02方式铣削圆弧的轮廓，也可以采用直线拟合方式。采用直线拟合法逼近的方式，需要合理构建三角函数数学模型，如图2-11所示得到X=R∗COS（α）、Y=R∗SIN（α），其中R为圆的半径值，找出变量之间的关系，用G01进行拟合，具体的编程思路如图2-12所示。

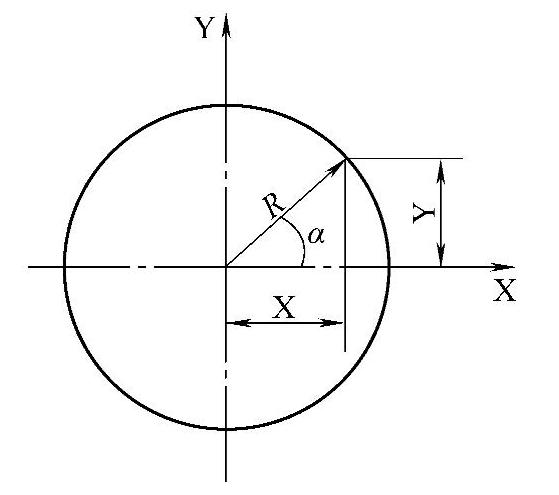
图2-11 基于圆的三角函数数学模型示意图

（4）变量的设置：#103号变量控制深度方向的变化；#100号变量控制圆的半径；#101号变量控制毛坯余量的变化。先编写轮廓精加工程序；在精加工程序的基础上，利用#103号变量实现分层铣削；在实现分层铣削基础上再结合#101号变量，实现去除余量的分层轮廓粗铣加工。

第1章已经详细介绍铣削平面的宏程序编程，本实例不再给出分析过程以及相关代码，具体请参考1.4节所叙的相关内容。

2.程序流程框图设计

根据上述分析，规划的精加工刀路轨迹如图2-13所示，规划的分层铣削刀路轨迹如图2-14所示，分层铣削过程的程序流程框图如图2-15所示。

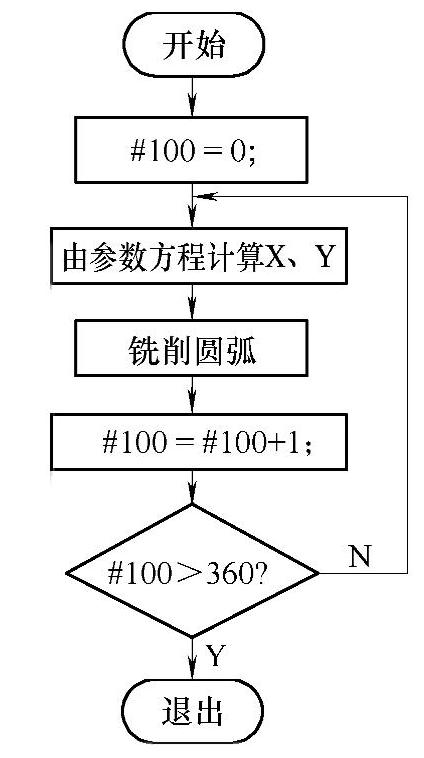
图2-12 铣削圆台流程框图

图2-13 精加工刀路轨迹示意图

图2-14 分层铣削刀路轨迹示意图

图2-15 分层铣削程序的流程框图

3.根据算法以及流程框图编写加工的精铣宏程序代码

O2019程序编程要点提示：

（1）关于G02、G03圆弧插补指令的补充说明：G02是在指定平面内进行顺时针插补的指令，G03则是在指定平面内进行逆时针插补。关于顺时针、逆时针的判断原则是：从第三轴的正方向向负方向看，顺时针用G02逆时针用G03。

（2）关于进刀方式的问题，涉及铣削加工的工艺问题，在此补充说明几点：

1）铣削平面零件时，一般采用立铣刀的侧刃进行切削。为了减少接刀的痕迹，保证加工零件表面质量，要充分考虑刀具切入和退出时对零件表面的影响。

2）铣削外表面的轮廓时，切入和退出点一般选择在零件轮廓曲线的延长线上，而不应该沿零件轮廓法向直接切入零件，以避免产生刀痕，如图2-16所示。

3）在铣削内轮廓时，由于零件的轮廓曲线无法延长，所以不能从外表面切入零件和退出零件，而采用圆弧过渡切入和退出方式，如图2-17所示，当实在无法沿零件曲线的切向切入、切出时，铣刀只有沿法线方向切入和退出零件，在这种情况下，切入、切出点应选在零件轮廓两条棱边的交点上，而且在进给过程中要避免停顿。

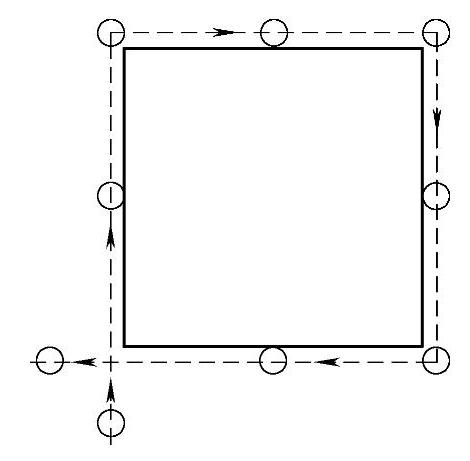
图2-16 外轮廓切入、退出零件方式

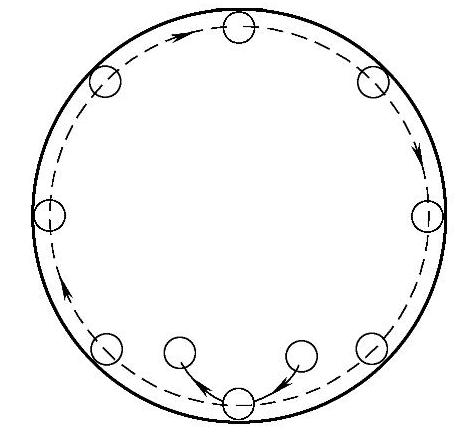
图2-17 内轮廓切入、退出零件方式

程序O2019采用圆弧切入和退出零件的进退刀方式来保证零件表面质量，例如：

G03X[#100]Y0R5，该语句是采用1/4圆弧过渡切入零件；

G03X[#100+5]Y-5R5，该语句是采用1/4圆弧过渡退出零件。

采用图2-11建立数学模型的算法来实现铣削圆的宏程序代码如下：(www.xing528.com)

O2020 程序编程要点提示：

（1）关于数学模型建立的问题。

数控加工采用宏程序编程时，往往需要根据零件图来构建数学模型，基于数学模型结合数学知识（如三角函数、线性方程、解析几何等相关知识）找出变量之间的关系。

数学模型建立是否合理，往往决定了程序设计算法的优劣，如图2-11所示建立的基于圆三角函数关系模型，解题思路有以下两种：

1）根据圆的标准方程：圆的标准方程为（X-X₀）2+（Y-Y₀）2=R²，其中（X₀，Y₀）为圆心的坐标，R为圆的半径。

在本实例中圆心的坐标为（0，0），该圆的方程为X²+Y²=R²，设置#100变量表示圆弧上各点X值，#101号变量为圆弧上各点Y值，#100号变量和#101号变量之间的关系满足圆方程的表达式。

读者也可以根据上述分析，设计算法并写出程序设计的流程框图，编制宏程序代码。

2）根据圆的参数方程，圆心在（X₀，Y₀）处的参数方程为：

在本实例中圆心坐标为（0，0），R为常量，数值是50，设置#100号变量为角度变量，赋初始值为0°，铣削的是整个圆弧轮廓，可见角度变化为0°～360°。

圆弧上各点X值和Y值，可以根据圆的参数方程计算出，如本程序中用语句#101=50∗COS[#100]表示圆上各点X值，用#102=50∗SIN[#100]表示圆上各点的Y值；利用G01直线插补指令G01 X[#101]Y[#102] F150铣削一小段圆弧，通过角度从0°～360°的变化，以及语句#100=#100+1和IF[#100 LE 360]GOTO 10来控制整个圆弧的铣削过程。

（2）本实例中采用圆的参数方程表达式来建立数学模型，可以通过控制角度的变化，实现任意圆弧段的切削。如起始角度为0°，终止角度为180°，铣削出半圆。

圆弧加工的精度取决于角度增量的大小，角度增量越小，精度越高。如采用圆的标准方程来计算圆弧上X、Y各点坐标，计算量相对会大。如果铣削的不是整个圆弧轮廓，不如采用圆参数方程控制方便，因此，建议（而不是规定）在编制此类数控铣宏程序时应优先考虑用圆的参数方程来构建数学模型。

（3）该实例程序没有实现分层铣削圆弧轮廓，也没有实现粗铣圆弧轮廓，适用于圆弧轮廓的精加工。

关于该实例分层铣削圆弧宏程序代码的编写，可以参考图2-14分层铣削圆弧轮廓刀路图以及图2-15分层铣削刀路程序流程框图的设计，也可以参考实例2-1中的O2012宏程序代码。

整个圆弧轮廓粗加工宏程序编制的思路：在圆弧精加工轮廓和分层铣削方法的基础上，在圆弧X向增加一个变量来控制每一层铣削毛坯余量的变化，规划刀路轨迹如图2-18所示，程序设计的流程如图2-19所示。

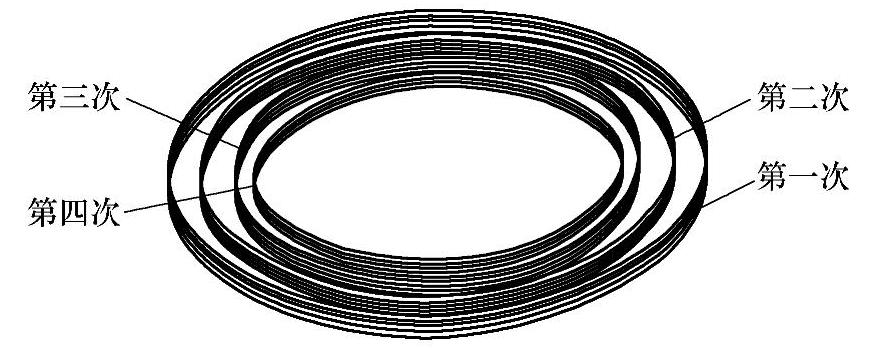
图2-18 分层粗铣刀路示意图

粗铣圆弧余量的计算方法为：粗加工余量=（毛坯的尺寸-零件轮廓的尺寸）/步距。为了防止得出的结果有小数或除不尽，机床运算会自动保留有效位，这样会产生计算的误差，需要采用FIX函数即上取整函数来保证计算精度，从而保证零件尺寸精度。

本实例中从毛坯图形分析，毛坯为直径150mm、长度60mm的圆柱体，刀具是直径为12mm的立铣刀，为了避免全刃切削，步距采用固定值10mm，加工余量计算如图2-20所示。

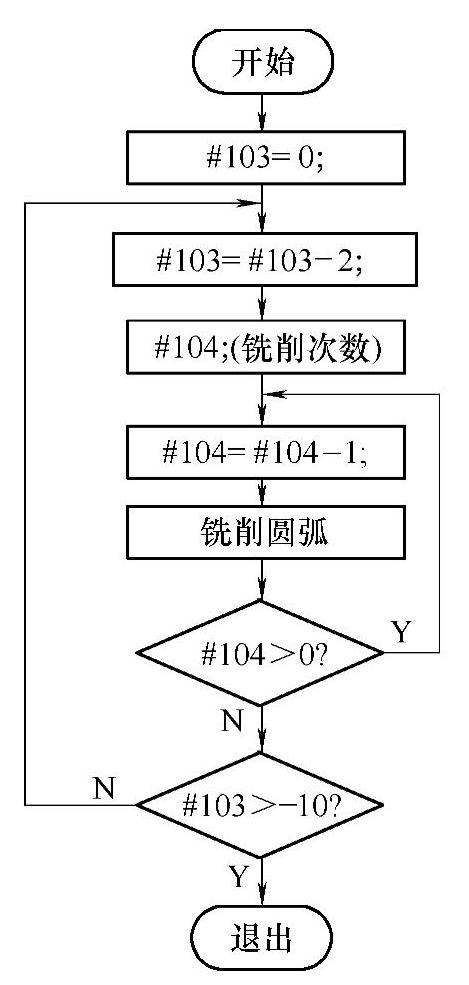
图2-19 分层粗铣流程框图

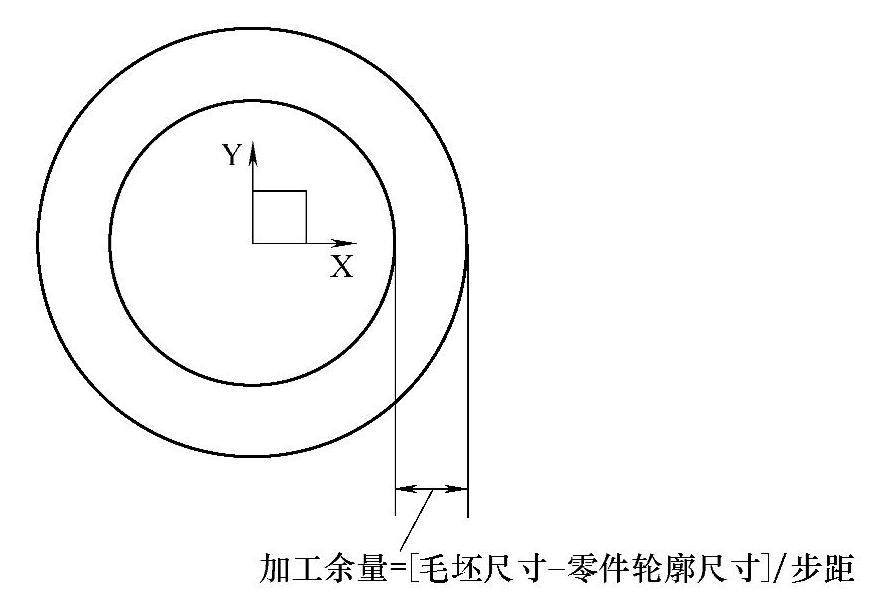
图2-20 余量计算示意图

根据以上分析编制宏程序代码如下：

O2021 程序编程要点提示：

（1）此程序是基于图2-11所示的数学模型，实现了分层铣削圆弧的粗加工，适用于毛坯的粗加工，该程序留有5mm的精铣余量。

（2）本程序通过将精加工轮廓的刀路轨迹进行等距偏移，来实现粗铣轮廓，每层平移的总量就是该层零件毛坯的尺寸减去零件轮廓的差值，在本实例中每层偏移的总量相等。如果每次偏移的总量不相等（如球体的粗加工、椭圆球体的加工等），则相对复杂得多，在此不再深究。

（3）补充说明FIX和FUP函数的用法和处理过程：无条件舍去小数部分，称为上取整函数；小数部分进位到整数部分为下取整函数（这和数学上四舍五入的规定是不完全相同的），在此要特别注意对负数的处理。例如：设变量#100=1.2和#101=-1.2；FIX[#100]=1；FIX[#101]=-1；FUP[#100]=2；FUP[#101]=-2；