直流分量注入的危害、成因及解决方法

9.1.1.1 直流分量注入的危害及成因

直流电流注入电网会产生极大危害。直流电流注入电网，首先影响的就是各级变电站中的变压器设备。直流电流的注入会引起变压器的直流偏磁。直流偏磁导致变压器励磁电流和谐波电流的急剧增加，可能引起变压器铁心磁饱和，导致铁心的磁致伸缩。同时在周期性变化的磁场作用下，硅钢片会改变尺寸，引起振动和噪声。而磁致伸缩产生的振动是非正弦波的，变压器噪声的频谱中含有多种谐波分量，并且随着磁通密度的增大而增大。直流偏磁引起的高振动对变压器的危害很严重，可能会引起变压器内有关部件的松动，进而威胁变压器的安全运行。由直流偏磁引起的谐波电流是危害性很大的偶次谐波电流，电能质量规范中有关偶次谐波电流的规定比奇次谐波更加严格。直流电流并入电网，还可能直接供应给交流负载，直流分量会造成电流的严重不对称，损坏负载。

在理想情况下，逆变器的输出电压和输出电流都是标准的交流信号，不存在直流分量问题，因此在并网逆变器的设计中往往会忽略这方面的问题。在工程实际中，直流分量注入已经成为光伏并网发电装置的一个重要指标。IEEE Std 929-2000和IEEE Std1547-2003明确规定，并网发电装置向并网注入的直流电流分量不能超过装置额定电流的0.5%。

逆变器的输出电流中直流分量的原因有两种类型：一种是可控的，另一种是不可控的。以电压型逆变器为例，如图9-1所示。由于同一半桥上下两个器件不能同时导通，为此通常要在开关信号中加入死区时间，即让需要关断的器件先关断，关断以后再开通需要开通的器件。死区时间的加入，使原本应该完全互补工作的两个器件实际上并非完全互补，这就造成了输出电压/电流的不平衡，也就产生了直流分量。上述例子是电压型变流器，对于电流型变流器也存在类似问题。电流型变流器为了保证直流侧电感有续流通道，电流型变流器同一半桥上下两个器件在换流时刻还必须同时导通一定时间，即所谓叠流时间，叠流时间也同样会产生直流分量。这种由死区（叠流）时间造成的直流分量可以通过减小死区（叠流）时间或采用无死区（叠流）工作方式加以抑制乃至消除，因此这种类型的直流分量是可以控制的。除了死区以外，基准信号中的直流偏置、控制电路中运算方法器的零漂等都属于这种造成直流分量的原因。

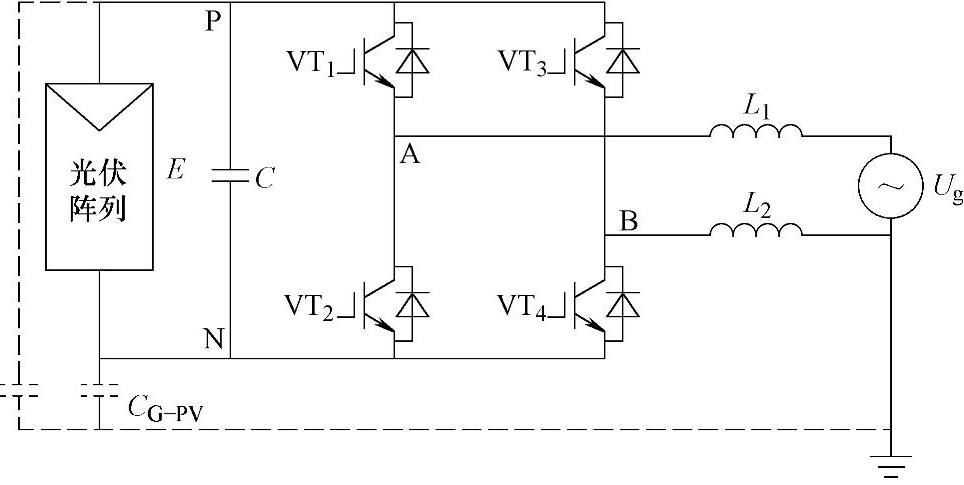
图9-1 单相全桥并网逆变器

在理想情况下，各开关器件的动、静态工作特性完全一致，电路中的线路阻抗也完全对称，没有寄生参数和寄生电磁场的影响。而在工程实际中，上述理想状态是根本不存在的。最典型的就是器件特性的分散性。即使是同一流水线上同一批次生产的两只器件，也不可能做到其动、静态特性完全一致。仍以图9-1为例，四个器件的开关时间、导通电阻等不可能完全一致，因此必然会造成输出信号中有直流分量存在。这种原因造成的直流分量是无法彻底消除的，也不是通过简单的手段就能控制的。

9.1.1.2 解决直流分量注入问题的方法

解决直流分量注入问题的一种方法是采用可以直接屏蔽直流分量的逆变器拓扑结构。图9-2所示的半桥逆变电路就是这样一种电路结构。在半桥逆变器中，由于电容的隔直流作用，输出电压中的直流分量（不论何种原因产生）都会被自动平衡，因此不会发生变压器的直流偏磁和磁饱和问题。

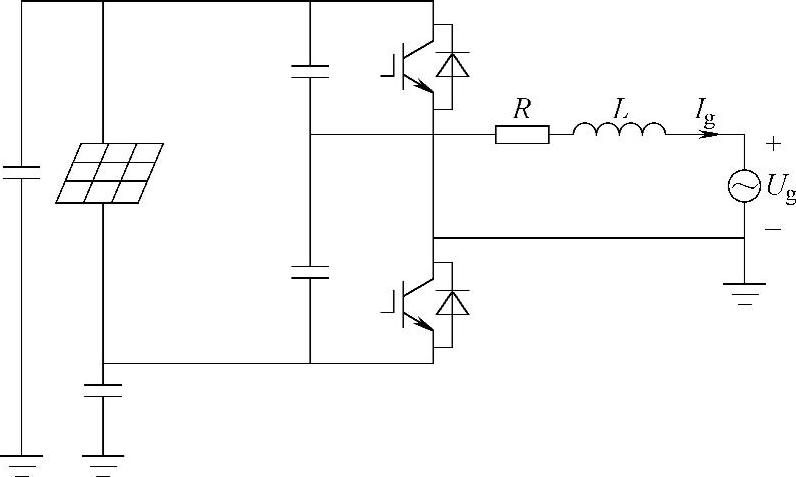
图9-2 半桥结构的光伏并网逆变器

半桥电路虽然能够解决直流分量注入和共模漏电流的问题，但其开关的利用率较低。要想达到与全桥逆变器相同的输出功率，其直流侧电压必须提高一倍。而单相全桥逆变器是中小功率电力电子装置中应用最为广泛也最为成熟的。大量的直接并网光伏逆变器产品采用这种拓扑结构。因此在不改变拓扑结构的基础上，寻求新的控制策略解决直流分量注入问题就非常有必要。下面给出这样一种新型的控制策略。

实际上解决直流分量注入问题最简洁的手段就是在输出回路中串联一个电容，如图9-3所示。

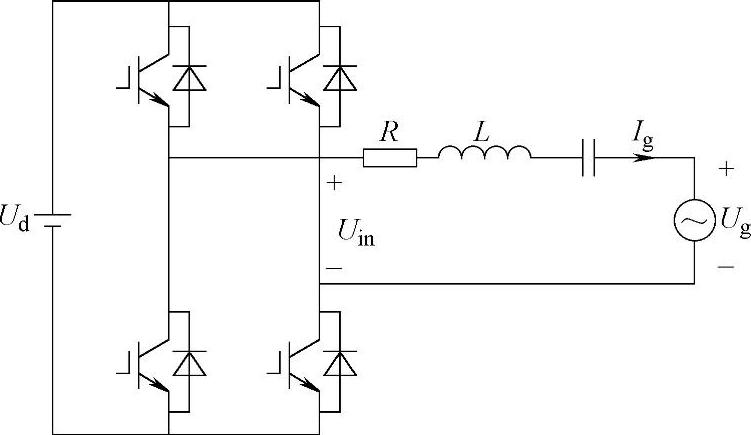
图9-3 输出回路串入电容的单相全桥并网逆变器

由图9-3可列出串入电容后系统的负载特性：

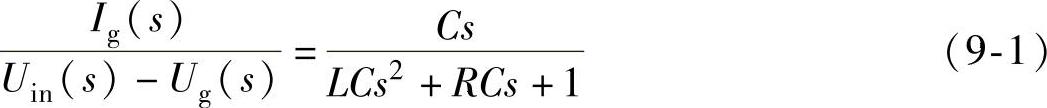
并网逆变器按照电流模式控制，并且忽略逆变器的小时间常数，则其控制框图如图9-4所示。其中K为逆变器等效放大倍数，G（s）为控制传递函数。根据经典控制理论，可对图9-4进行如图9-5所示的等效变换。

注意图9-5虽然与图9-4完全等效，但对应的电路结构却大有不同。即无需向图9-3中那样在输出回路中串入实际的电容，只要通过一定手段，即可实现图9-5所示的控制框图，相当于串入电容。可对图9-5作进一步变换，如图9-6所示。

比较图9-6与图9-4、图9-5可以发现，点画线框内的结构已经和图9-1所示的常规单相逆变器完全相同。对常规单相全桥逆变器施加如图9-6所示的控制方法，就可以等效于在(www.xing528.com)

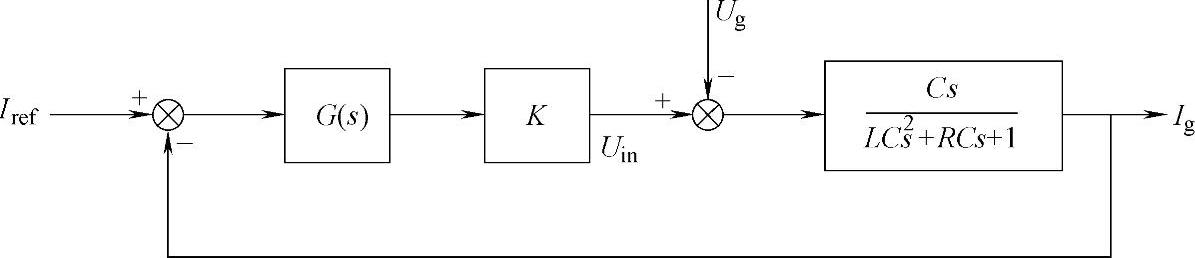
图9-4 图9-3单相全桥并网逆变器的并网闭环控制框图

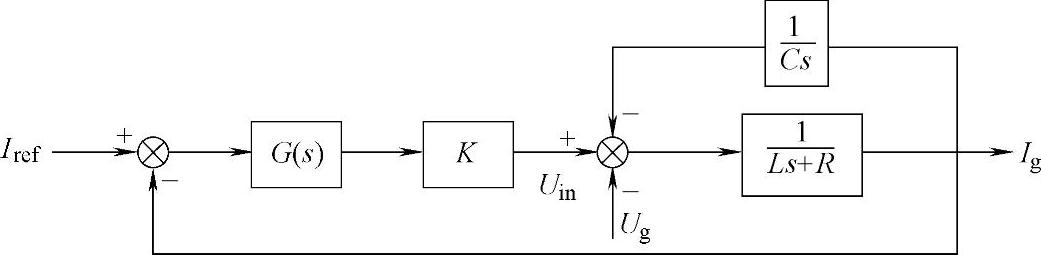
图9-5 图9-4的等效变换

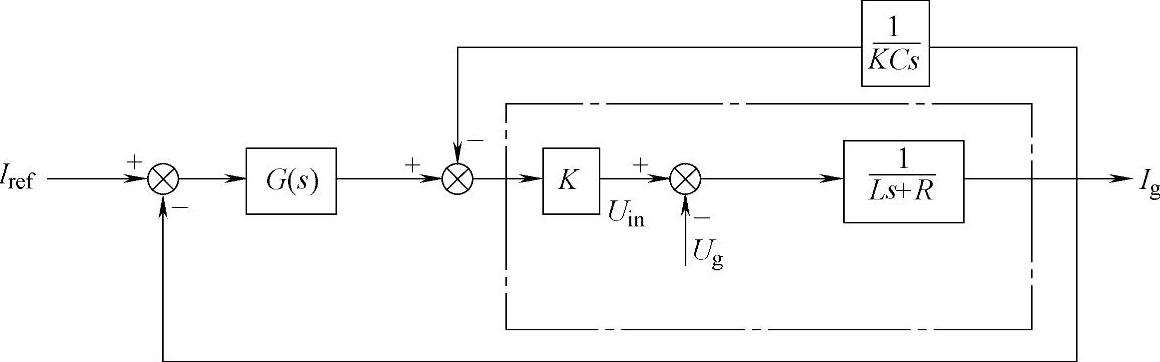
图9-6 对图9-5的进一步变换

输出回路中串联了电容，这种方法可称为“虚拟电容法”。图9-6所示控制系统的闭环传递函数为

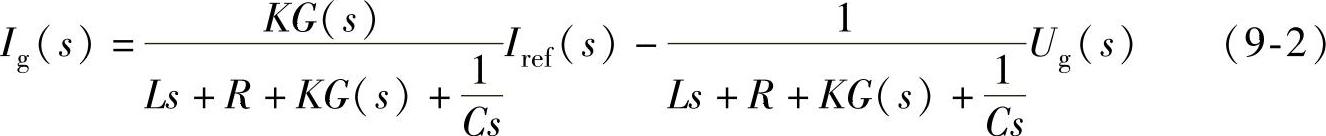
为了消除交流稳态误差，图9-6中的控制器可采用比例复数积分控制器。

为了验证上述方法，进行了系统仿真。

首先假设电流给定I_ref中含有直流分量，采用无虚拟电容的控制算法，逆变器输出电流及其频谱如图9-7所示。由图9-7可见，无虚拟电容时，闭环系统不能消除由给定电流造成的直流分量。当其他条件不变时，采用有虚拟电容的控制算法，逆变器输出电流及其频谱如图9-8所示。由图9-8可见，直流分量已经被完全消除。

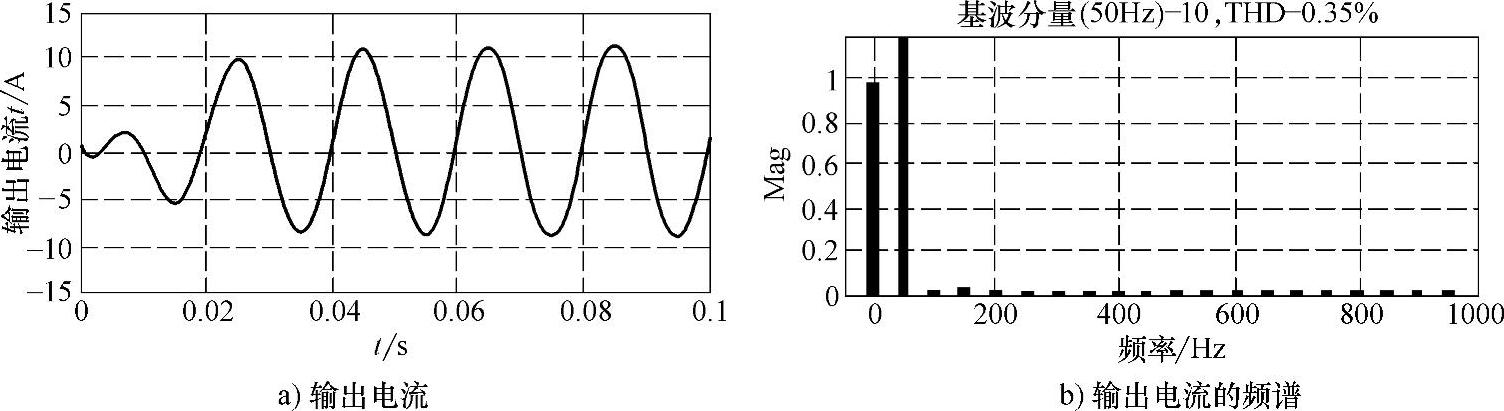
图9-7 无虚拟电容时，逆变器输出电流及其频谱（电流给定含直流分量）

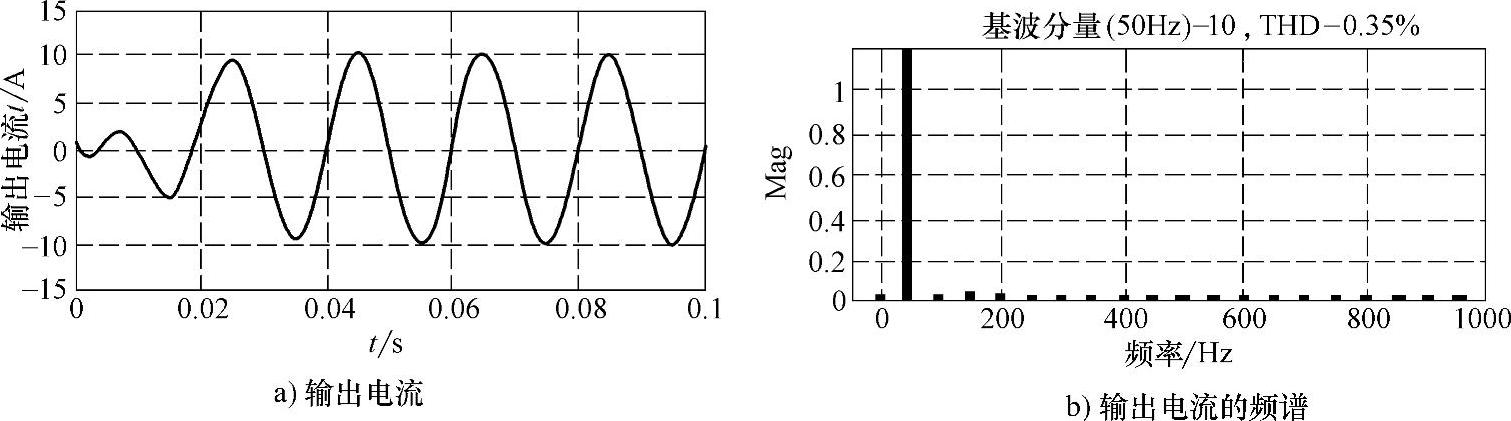
图9-8 有虚拟电容时，逆变器输出电流及其频谱（电流给定含直流分量）

再假设电网电压中含有直流分量，采用无虚拟电容的控制算法，逆变器输出电流及其频谱如图9-9所示。由图9-9可见，输出电流中没有直流分量。即使电网电压中含有直流分量，也能够采用虚拟电容法消除输出电流中的直流分量。

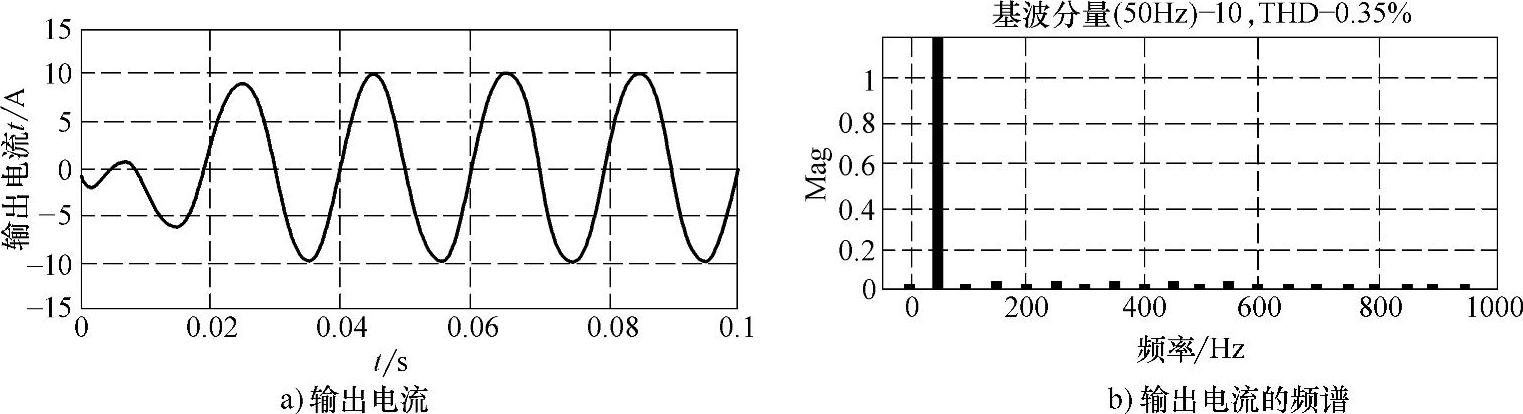
图9-9 无虚拟电容时，逆变器输出电流及其频谱（电网电压含直流分量）

通过以上仿真分析可以证明，虚拟电容法对直流分量的抑制作用是明显有效的。