自适应模糊控制法：优化方案

模糊控制器的设计主要包含以下几个主要内容：确定模糊控制器的输入变量和输出变量；归纳和总结模糊控制器的控制规则；确定模糊化和反模糊化的主要方法；选择论域并确定相关参数。使用模糊逻辑方法进行光伏系统的MPPT控制具有较好的动态性能和精确度。

模糊控制器的两个输入量分别为误差e（kT）和误差变化Δe（kT）其表达式如下：

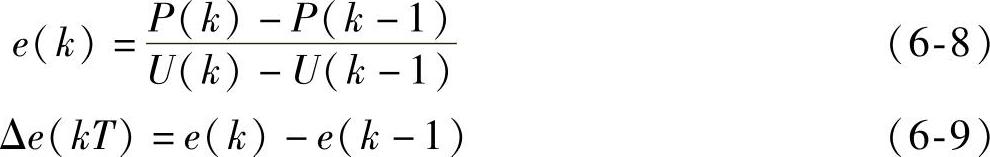
自适应模糊控制是在常规模糊控制方法的基础上增加了性能测量、控制量校正、控制规则修正等功能模块。其结构框图如图6-10所示。

为了测量系统性能，需要对系统进行采样。每次采样的时间响应可以通过监测e（kT）和误差变化Δe（kT）获得。将实际响应和希望响应相比较，就可以进行衡量控制器性能，确定输出响应的校正量p，以便为控制规则的修正提供信息。输出响应的校正量可通过查判定表得到，通常判定表是由e（kT）和误差变化Δe（kT）进一步制定出来的。

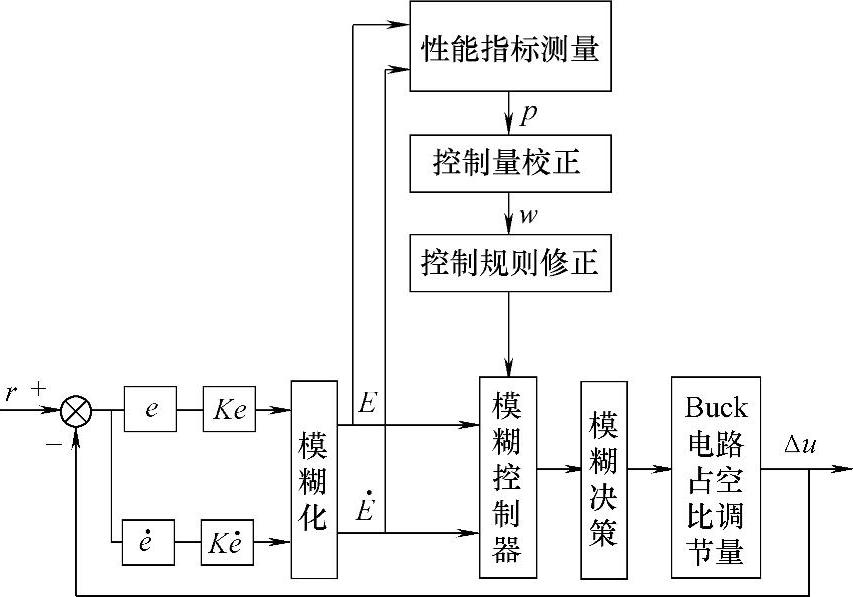
图6-10 自适应模糊控制结构框图（以Buck电路为例）

控制量校正通过上述的性能测量得到了光伏系统达到最大功率点所需的输出响应的校正量。为了实现自适应控制，需将输出响应的校正量p转换为对控制量的校正量w，也需要控制对象的特性，即控制对象的增量模型J（其中表示控制对象输出对输入Jacobian矩阵）。从而求出相应于控制输入的修正量为

W_i（kT）=J^-1W_o（kT） （6-10）

式中，W_o（kT）为输出修正量；W_i（kT）为输入修正量。

控制规则的修正就是利用得到的控制输入的校正量来修改控制规则，以此改善控制性能。对光伏系统来说，假定在前d次采样中使系统的工作点偏离最大功率点（由外界环境的变化或系统自身的控制规则导致）或使系统在最大功率点产生大的振荡，即使系统性能变差，则那时的误差、误差变化率和控制输入量为e（kT-dT）Δe（kT-dT）u（kT-dT）。根据已求得的控制输入校正量W_i（kT），控制输入应当取为u（kT-dT）+W_i（kT）。针对相应论域中的这些量，构造模糊集合为(www.xing528.com)

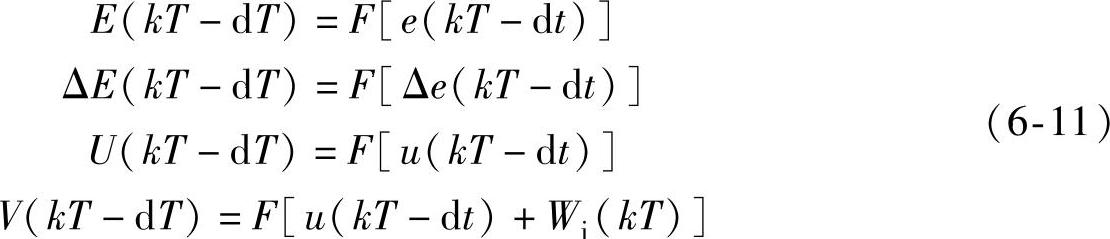
原来的模糊规则为

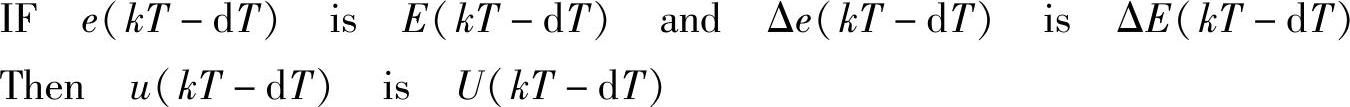
修改后的规则变为

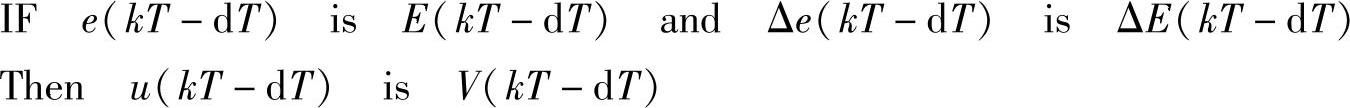
为了实现这种控制规则可以用如下矩阵运算：

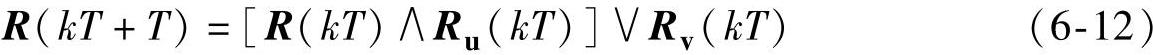
式中，R（kT）为修正前的模糊关系矩阵；R（kT+T）为修正后的模糊关系矩阵。

通过增加的3个自适应控制功能模块，就可实现根据检测到的外界环境的变化，来修正控制规则及减小普通控制方法在最大功率点的波动现象。在光伏系统中，最大功率点的跟踪速度和跟踪精度是控制系统的关键因素，这些因素与系统调节的步长有直接关系。当系统的工作点远离最大功率点时，必须加快跟踪速度，即加大调节的步长Δu；当系统的工作点在最大功率点附近时，为了系统的跟踪精度和稳定，必须适当减小调节的步长Δu，避免使系统在最大功率点附近振荡。