光伏电池板最大功率点跟踪的扰动观察法及优化策略

扰动观察法，又称爬山法，由于其结构简单，需要测量的参数较少，所以它被普遍应用于光伏电池板的最大功率点跟踪。其原理就是要引入一个小的变化，然后进行观测，并与前一个状态进行比较，根据比较的结果调节光伏电池的工作点。具体做法是通过改变光伏电池的输出电压，并实时地采样光伏电池的输出电压和电流，通过DSP计算出功率，与上一次计算的功率进行比较，如果小于上一次的值，则说明本次控制使功率输出降低了，应控制使光伏电池输出电压按原来相反的方向变化，如果大于则维持原来增大或减小的方向，这样就保证了使太阳能输出向增大的方向变化。如此反复的扰动、观测与比较，使光伏电池板达到最大功率点，实现最大功率的输出。图6-3所示为扰动观察法的流程图。

当采用定步长的扰动观察法时，步长越短，光伏系统在最大功率点附近振荡的幅度越小，能量损失越小，但达到最大功率点需要扰动的次数就越多，所用的跟踪时间也越长。反之当步长较长时跟踪速度快，但在最大功率点附近波动幅度大，能量损失也严重。因此光伏系统最大功率点跟踪的速度和稳态精确度难以同时保证，只能根据实际需求折中选取扰动步长，以获得可接受的动态和稳态性能。为了解决常规定步长扰动观察法的跟踪速度与稳态跟踪精度之间的矛盾，可以采用定电压启动的自适应变步长算法。以光伏阵列的开路电压和短路电流为参考，标定之后的I-U、P-U和|dP/dU|-U特性曲线如图6-4所示。

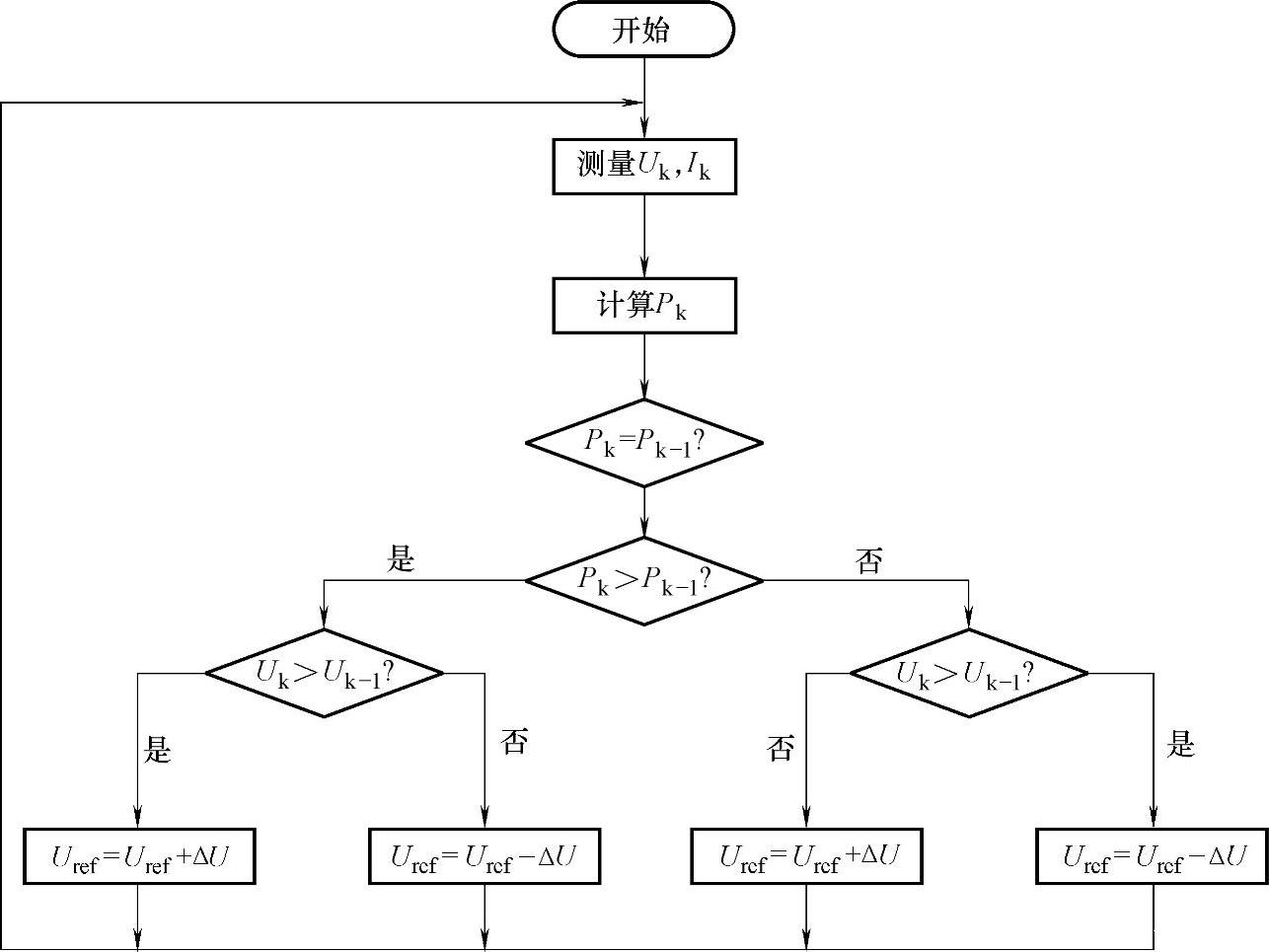
图6-3 扰动观察法控制流程图

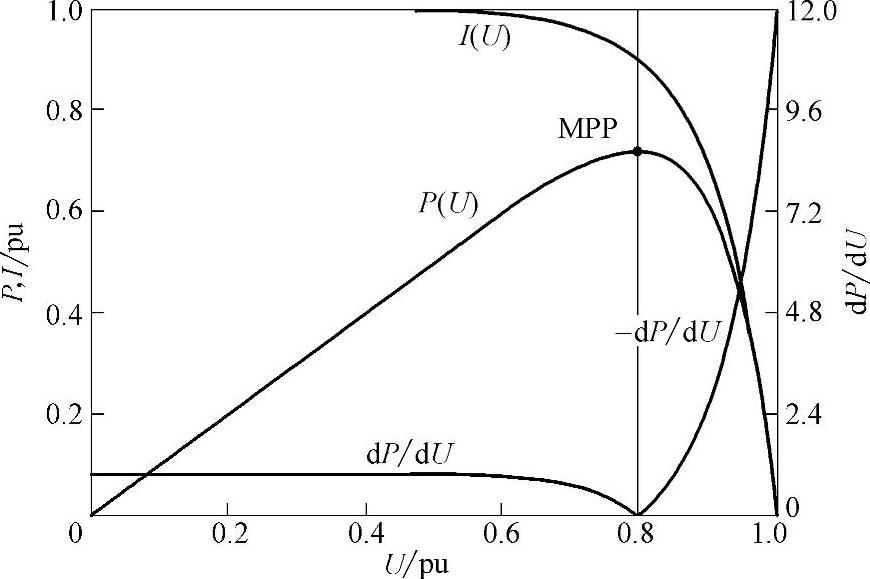
图6-4 光伏阵列定标后的I-U、P-U和|dP/dU|-U曲线

由图中可以看出，光伏阵列的dP/dU曲线有如下特点：

且无论在最大功率点的左侧或者右侧，随着逐渐接近最大功率点，|dP/dU|均单调递减，当到达最大功率点时，|dP/dU|为零。根据光伏阵列的这一内在特性，可构造电压扰动表达式为

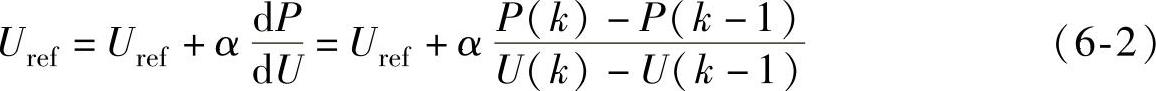
式中，α为正数，即变步长速度因子，用于调整跟踪速度。(www.xing528.com)

由式（6-2）可以看出，当光伏阵列运行点远离最大功率点时，跟踪步长大，反之步长小，在接近最大功率点时趋近于0。α可由下式确定

式中，U_{step_max}是定步长扰动观察法允许的最大步长，|dP/dU|_max可根据光伏阵列的特性计算，也可由下式估算

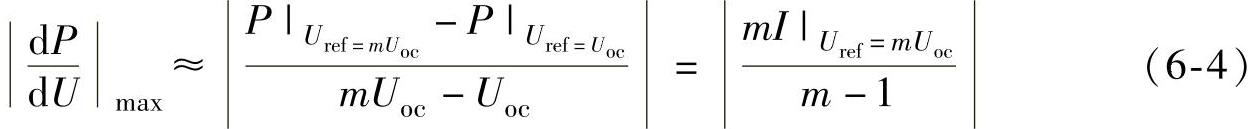
式中，m为接近于1的正数，例如0.98；U_oc为光伏阵列的开路电压。变步长速度因子α由式（6-3）计算其范围，再通过实验调整决定其最终的取值。

变步长扰动观察法的算法流程如图6-5所示。其中m为接近于零的很小的正数，在程序中用于判断U（k）与U（k-1）之差是否为零。当U（k）与U（k-1）之差不为零时，则根据式（6-2）自适应地调整扰动步长，如果U（k）与U（k-1）相等则结束返回。该程序以一定的时间间隔（即扰动周期）周期性地执行。

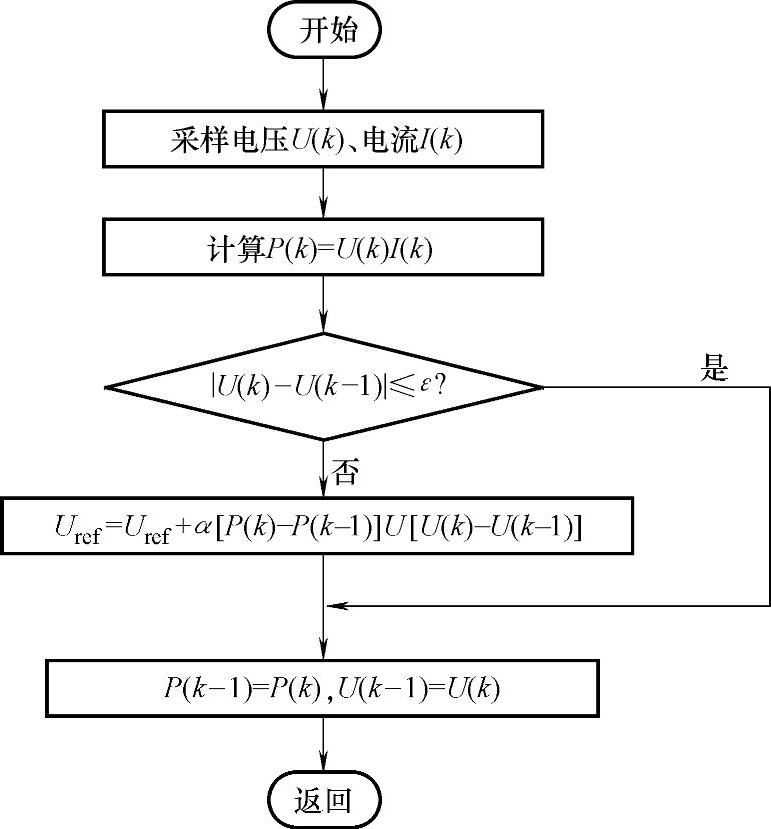
图6-5 变步长扰动观察法的算法流程图

光伏系统通常从光伏阵列的开路电压处开始启动，由图6-4可见，在光伏阵列的开路电压附近有一段恒压区，此时由于检测误差或者纹波等因素引起的微小电压变化能引起|dP/dU|很大的变化，从而影响扰动步长的准确性。为了避免这个问题，提高算法的可靠性，采用固定电压启动的方式，其流程如图6-6所示。由于光伏阵列的最大功率点近似为开路电压的0.78倍，因此定电压指令设为0.78U_oc，流程中e为接近零的较小的正数。该启动策略在系统运行之前首先检测光伏阵列的开路电压，然后将电压指令设置为开路电压的0.78倍，将运行点快速调整到最大功率点附近，确保系统正确平稳的启动。启动完成之后即可进入图6-5所示的变步长扰动观察算法流程。