并网逆变器直流侧控制优化

在前面介绍的逆变器并网控制策略中，大多有一个隐含假设，即直流侧电压是稳定的恒定的电压。而事实上在光伏发电系统中，光伏阵列的输出电压是随环境因素变化的，因此直流侧电压稳定的恒定的假设就成了问题。直流侧电压不稳定，或者说直流侧电压有波动，会导致低次谐波分量渗入交流网侧，造成波形畸变。

为了解决这一问题，有两种思路。一种是在直流侧设置平波环节。常规上，电压型逆变器的直流侧都要并联电容进行滤波，但电容滤波对低频信号的作用有限，且在体积、效率和成本等方面都存在问题。在光伏系统中，通常在光伏阵列与逆变器之间加入一级DC-DC变换器，也可以通过这个DC-DC变换器实现稳压，这就是光伏系统的所谓恒压控制。恒压控制在一定条件下，可以使光伏系统工作在最大功率点附近，因此也是目前光伏并网逆变器中最常用的控制方案。但恒压控制不能保证光伏系统在环境条件大幅度变化时的最大功率点跟踪控制。如果采用最大功率点跟踪控制方案，则逆变器的直流侧电压又不能保持稳定。这时，可在直流母线上并联具有DC-DC变换器的储能系统，如蓄电池、超级电容和燃料电池等，利用这些储能设备平抑直流电压；但要完全实现平抑直流电压的功能，储能系统的容量会非常大。以上两种方案，是在直流侧设置平波环节的典型方案；除了这几种以外，还可以在直流侧设置直流有源滤波器。

解决直流侧波动问题的第二个思路是通过对逆变器的控制来实现直流侧电压的稳定。这也以下着重讨论的。在进行这方面讨论之前，先分析一下直流侧波动引起交流侧波形畸变的原因。

5.4.5.1 直流侧波动对交流侧波形的影响

1.定性分析

对于单相全桥逆变器而言，可采用单极倍频SPWM技术控制开关动作。在PWM中，一般载波频率远远大于调制波频率，即ω_c＞＞ω_m（ω_m为调制波角频率），在一个载波周期中，调制信号u_r可视为恒值。在实际系统中由于直流侧电压的脉动，按常规PWM算法进行调制时，因为载波和调制波不发生变化，所以开关时刻和开通时间不变，这样输出电压量就会在0和实际值E′=E±ΔE之间变化，直流侧的脉动就会被调制和传输到负载上。经过多电平电路的合成，输出侧的波形中就会产生低次谐波，造成波形畸变，如图5-42所示。

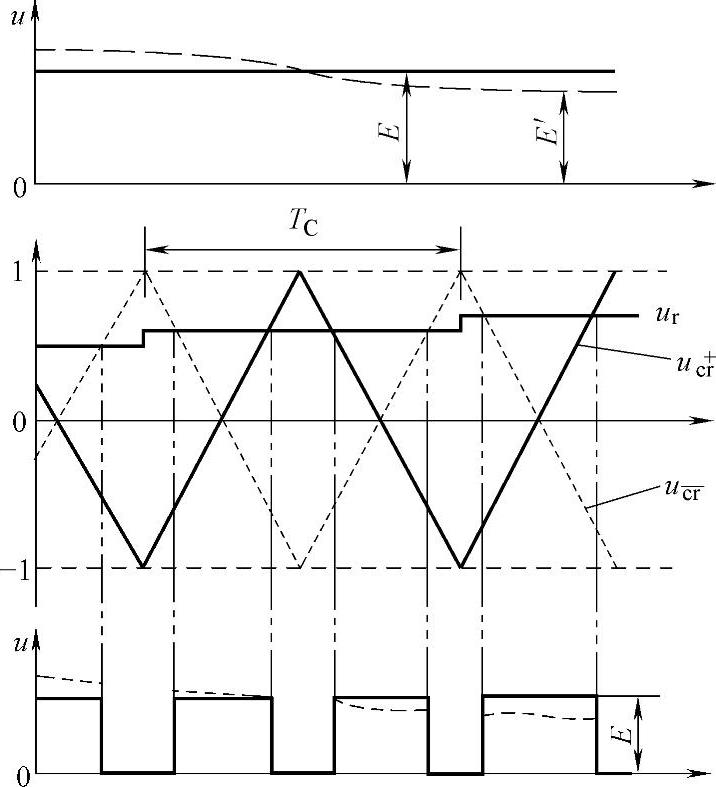
图5-42 波形畸变形成原理

2.基波、低次谐波的近似计算

用不控整流电路模拟直流侧电压波动，以下定量地分析其对交流侧电压的影响。当整流器直流侧的滤波电容由0～+∞时，其电压由M脉波（单相整流M=2）逐渐变为理想的无脉动的直流电压，如图5-43所示。

当滤波电容为0时，不考虑电网阻抗，负载使用电阻模型，不控整流器输出电压u_d（即图5-43中实线）的傅里叶级数可表示为

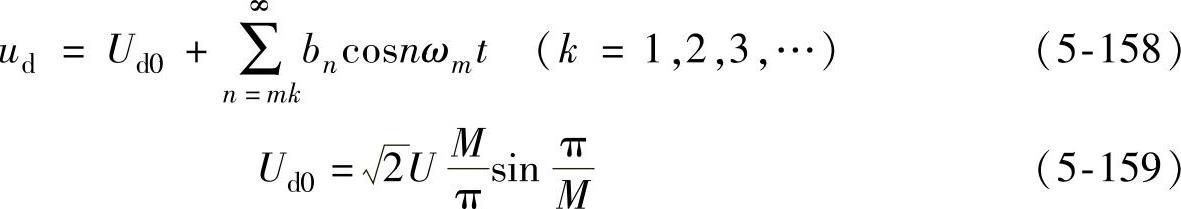
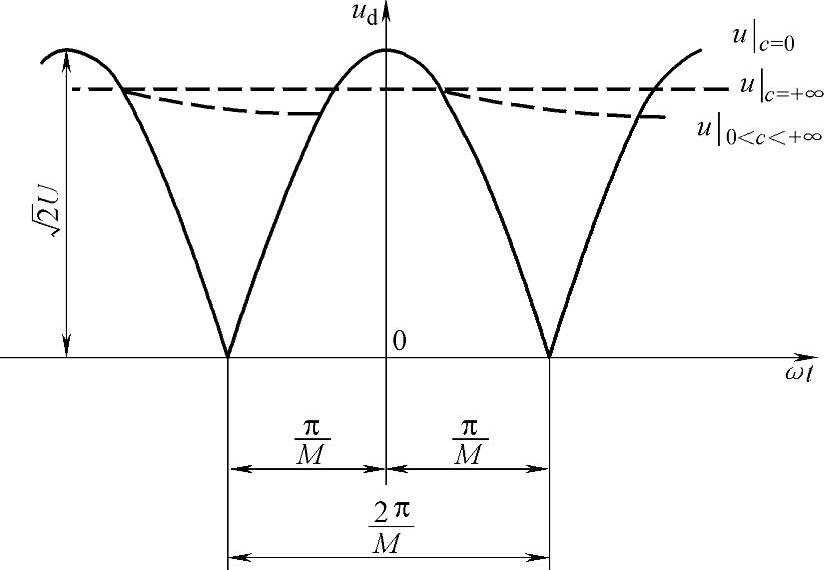
图5-43 M脉波整流器输出电压波形

而单极倍频SPWM下变流器交流侧电压（即图5-39中a、n两点间的电压）的傅里叶级数展开式为

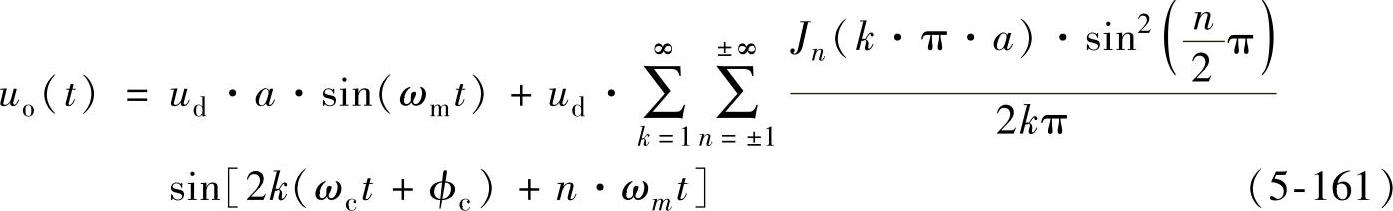
将式（5-158）代入式（5-161）中就可以得到由直流脉动造成的输出畸变电压的傅里叶级数，为

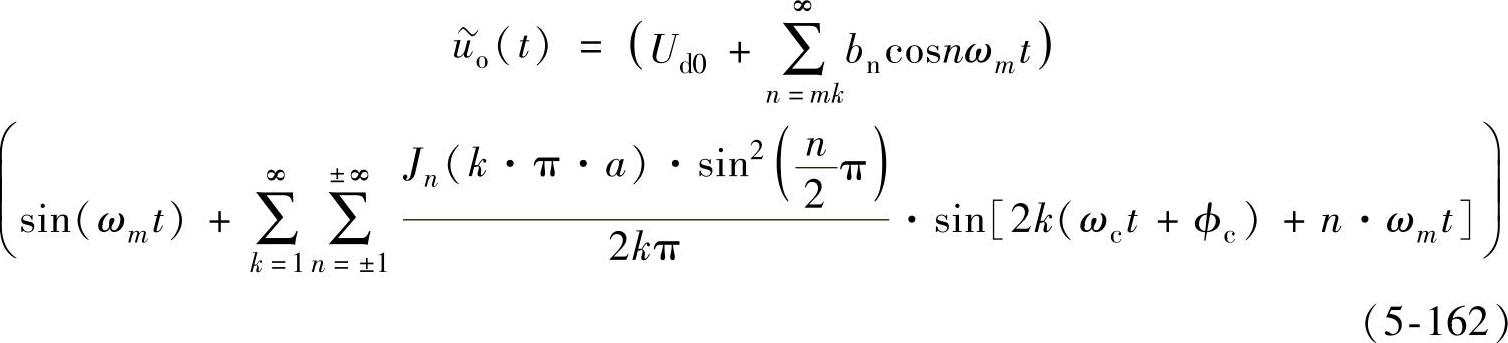
由式（5-162），当M=2即单相不控整流电路提供逆变器直流侧电压时，输出电压的基波幅值为

低次谐波分量（即n＜＜ω_c/ω_m）为

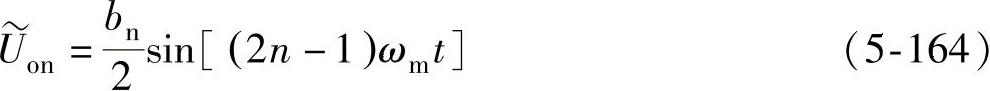
从式（5-163）和式（5-164）可见，当M=2时输出电压的基波幅值会有损失，同时频谱中会渗入低次谐波，最低次谐波的次数为3次。对于M＞2的情况，也可以根据式（5-162）推导得到，结论与M=2时大体相同，这里不多赘述。(www.xing528.com)

以上分析是当滤波电容为0时的分析，当滤波电容逐渐增大时，各低次谐波的幅值会逐渐降低但不会降到0；只有当电容增大到非常大时，才能消除直流脉动，但这显然会增加成本和体积。

上面的分析是以不控整流为例的，实际上光伏系统直流电压波动的频率可能要低得多，这时在交流侧就可能包含比基波频率还低的次谐波，其对电网的危害更大。

5.4.5.2 直流侧电压的闭环控制

要解决直流侧电压波动引起的交流侧波形畸变问题，通常的思路是实施直流侧电压的闭环控制。直流侧电压的闭环控制方案通常采用PI控制就能够满足系统要求，当然也可把某些其他控制策略如变结构控制、模糊控制等引入其中，比如前面提到的控制李亚普诺夫法就是一例。本节只介绍常规的工程设计法。

在设计电压环时，将设计好的电流环看成电压环的一部分，其工程设计法可以参照电流环的设计方法。一般情况下，因为电压环要求有较好的抗扰动性能，应当首先考虑将电压环设计为典型Ⅱ型系统。但这存在以下问题：

1）采用工程设计法设计的双闭环系统以稳定为主要出发点，兼顾动态特性，即稳中求快。但在电流环控制带宽有限的情况下，电压环的控制带宽会进一步降低。

2）在按照典型Ⅱ型系统设计电压环过程中，负载作为扰动处理，并没有出现在控制对象传递函数中，因此所建立数学模型存在较大偏差。

为了改善系统的动态特性，需要考虑负载阻抗的影响。此时电压环可以按照典型Ⅰ型系统设计，具体的设计方案可参照坐标变换法线性控制中电流环的设计。

5.4.5.3 载波幅值可调PWM技术及其在直流侧电压波动抑制中的应用

引入直流侧电压的闭环控制，可以非常好地实现直流侧电压的稳定，但这种方式使控制系统的阶数增高，增加了系统控制的复杂性。事实上，可以从PWM技术的基本原理出发，找出一种简单明快、可有效地解决直流侧电压波动带来的交流侧波形畸变问题的方法。

1.载波幅值可调PWM技术基本原理

规则采样法SPWM的基本原理如图5-44所示（u_g为调制波，在一个采样周期内可看作一条直线；实线三角形为载波其幅值为u_c；实线脉冲为输出电压波形，宽度为δ，高度为理想直流电压u_dc）。假设调制波为u_r=asinω_mt，其中a为幅度调制比。

当直流侧电压发生波动变为u′_dc时，如果仍按照原始算法给出触发脉冲，那么输出电压就发生了畸变。为了防止发生上述畸变，应该将脉宽δ调整为δ′，其调整的原则应满足伏秒等效原则，即

u_dc·δ=u′_dc·δ′ （5-165）

如果保持调制波和载波频率不变，要想得到δ′，载波幅值必须发生变化，即由图5-44中的实线三角形的u_c变为虚线三角形的u′_c。而u_c和u′_c的关系为

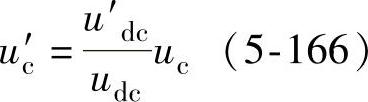
也就是说在考虑到直流电压脉动的情况下，应该按式（5-166）对载波幅值进行调节，这样就可以维持伏秒等效，消除直流电压脉动对输出电压波形的影响。这就是载波幅值可调PWM的基本原理。

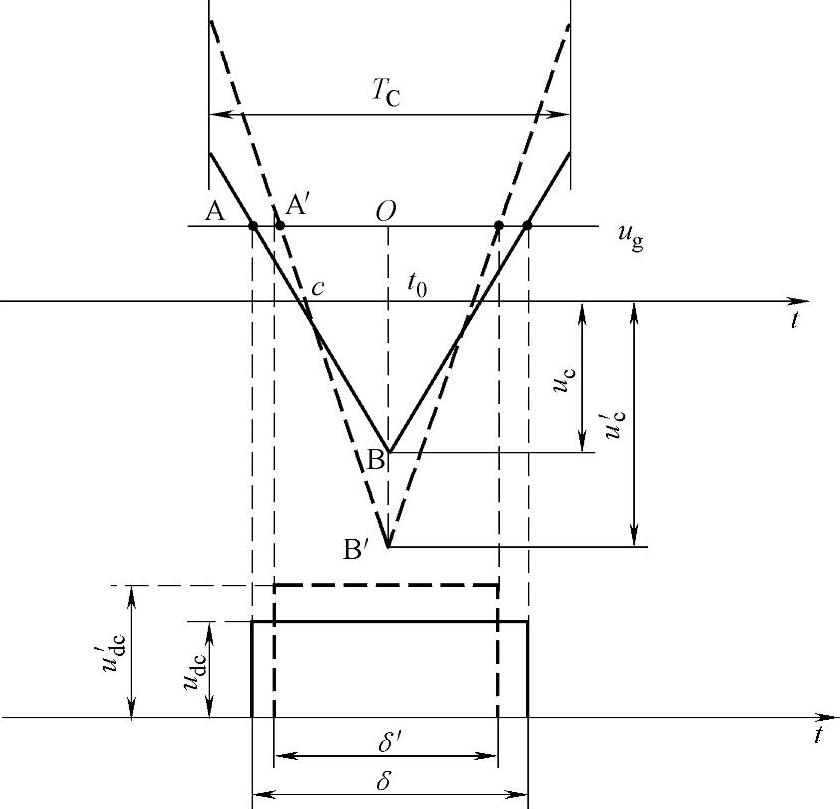
图5-44 脉动电压与载波幅值的关系

2.载波幅值可调PWM在直流侧电压波动抑制中的应用

在调制波正半周，假设某时刻直流侧电压变为E′=E+ΔE，由式（5-166）可知载波幅值增大，由图5-45可以看出VT₁、VT₄一起导通的时间减少。在此载波周期进行开关调制时，虽然直流电压增大，但通过减少开关管的导通时间，使总的伏秒与电压无波动时相同。因此也就抑制了因电压增大而产生的低次谐波，同时也使输出电压的基波达到理想的线性关系。同理，当直流侧电压减小变为E′=E-ΔE时，载波幅值降低，VT₁、VT₄一起导通的时间增加，总的伏秒仍与电压无波动时相同。同样也就抑制了因电压增大而产生的低次谐波，并使输出电压的基波达到理想的线性关系。调制波负半周的分析方法相同，这里不多赘述。

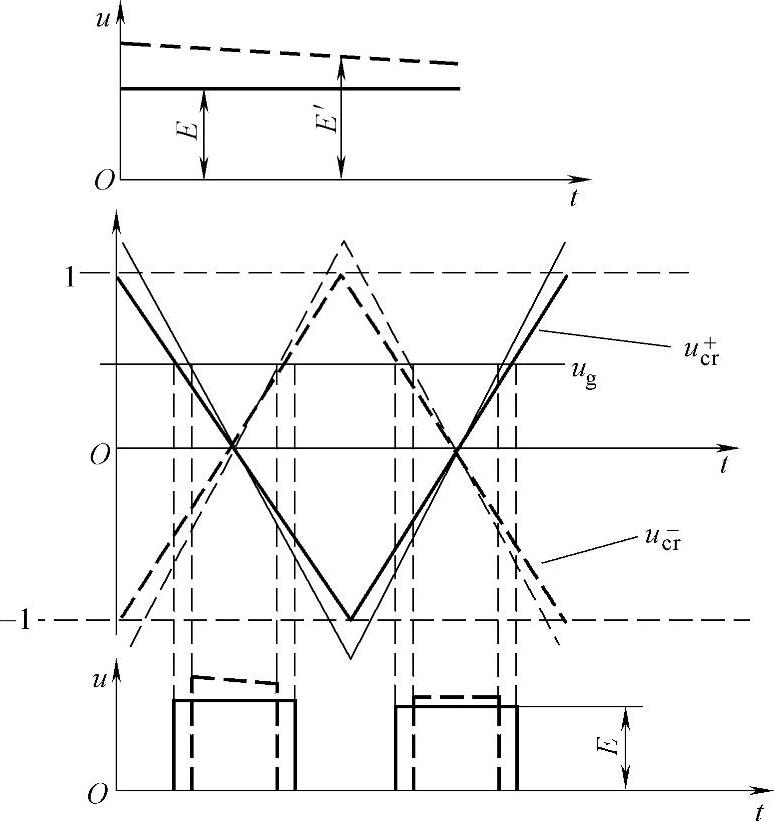
图5-45 幅值可调载波PWM抑制输出电压波形畸变的原理