非线性控制方法在并网逆变器中的应用

前面介绍的各种控制策略都是基于线性系统的。而并网逆变器本身由于电力电子器件的存在，它是一种强耦合、时变的非线性系统。正如前面介绍的那样，采用线性控制的手段控制逆变器，必须先提取逆变器的数学模型，并进行线性化。在这些过程中必须采取大量的近似和简化，因此最终得到的数学模型与实际系统存在非常大的偏差。为此，出现了非线性控制方法。非线性控制方法也有两种思路，一种是不需要提取数学模型，把逆变器当做“黑箱”，只对需要控制的信号实施直接的控制手段，滞环控制就是这种思路的典型方法；另一种是仍要提取数学模型，但无须对数学模型进行线性化近似，直接对非线性的数学模型采取控制，变结构控制是这种思路的典型方法。下面，分别对这两种方法进行介绍。

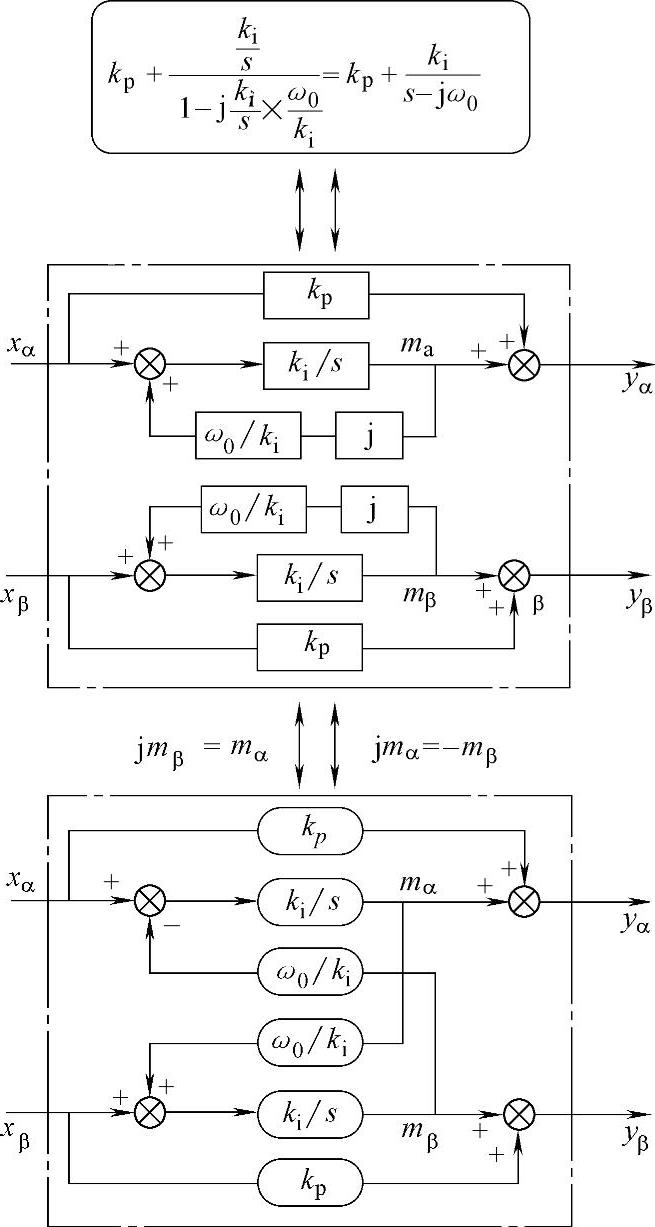
图5-35 比例复数积分控制的具体实现

5.4.4.1 滞环控制

滞环控制是一种应用广泛的闭环电流跟踪控制方法。滞环控制器具有闭环调节器和脉宽调制器的双重作用，可以将误差信号直接转换为开关的PWM控制信号。将其应用于单相并网逆变器电流控制的结构图如图5-36所示。通过同步电路和乘法电路获得与电网电压同频同相位的并网电流指令信号i^∗_g，与实际检测的并网电流i_g比较后获得的偏差Δi_g作为滞环比较器的输入，通过滞环比较器得到开关需要的PWM信号，从而控制并网电流。

由于开关频率远大于电网电压的频率，因此在一个开关周期可以认为电网电压u_g和给定电流i_g保持恒定，并且设滞环宽度为H。当开关管VT₁和VT₄导通时有

根据滞环比较的条件可以得到开通时间为

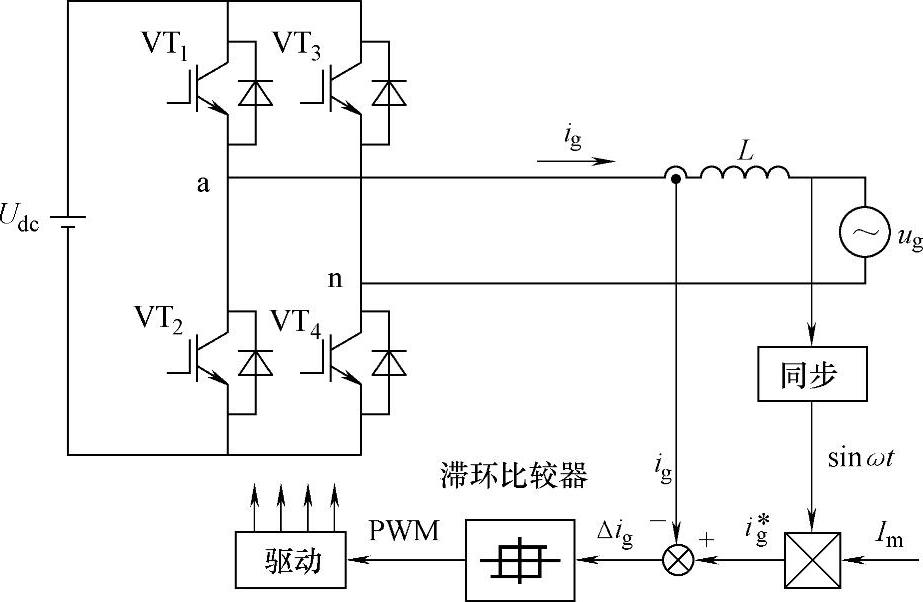
图5-36 单相并网逆变器的滞环电流控制

同理可得关断时间为

根据式（5-115）和式（5-116）可以得到开关频率为

通常逆变器输入电压U_dc可以认为是基本恒定，因此由式（5-139）可知，开关频率f_s与电网电压u_g、输出电感L和滞环宽度H有关。当电感L和滞环宽度H确定后，由于电网电压是按正弦规律变化的，因此开关频率是变化的。开关频率与下述因素有关：

1）开关频率与滞环宽度成反比，滞环越宽，开关频率越低。

2）变流器直流侧电压越大，交流电流变化率越快，开关频率也越大。在电网电压过零点时，开关频率最高，在电网电压峰值处，开关频率最低。

3）交流侧电感L越大，交流电流变化率越慢，开关频率也越小。

4）与参考电流的变化率有关，参考电流变化率越大，开关频率越小；参考电流变化率越小，开关频率越大。

可以根据需要的电流脉动量确定滞环宽度H，然后根据电路允许的最高开关频率和最低开关频率可以确定电感L。

滞环电流控制具有如下特点：

1）硬件电路简单；

2）属于实时控制方式，电流响应快；

3）不用载波，输出波形中不含特定频率的谐波分量；

4）属于闭环控制，跟踪性能好；

5）开关频率不固定，输出电流中谐波含量较多。

滞环控制也同样可以应用于电压跟踪控制。由于电压型逆变器的输出电压为PWM波，含有大量谐波，因此在实现电压滞环控制的时候，必须先对实际电压信号进行滤波处理。

滞环控制的开关频率不固定，严格意义上讲不属于传统的定频调宽PWM。不固定的开关频率使得滞环PWM在开关器件选择、滤波参数设计及热稳定性设计等方面都存在许多困难，因此在大功率电力变换器中应用非常有限。为此，很多开关频率固定或开关频率变化范围有限的新型滞环PWM技术被相继提出来，这些新技术正在研究和发展中。

5.4.4.2 单周期控制

单周期控制是一种优秀的跟踪控制策略。采用单周期控制实现三相逆变器并网，有以下优点：①控制电路结构简单（复位积分器和一些线性逻辑器件）；②动态响应快；③开关损耗低。在同一时间内，逆变器六开关只有两个开关动作，整流器六开关有四个动作。

对于并网型逆变器，要求输出电流畸变率低、功率因数高。一般方法是控制逆变器输出电流和电网电压同相，通过减小无功输出功率来达到最大有功功率输出。

为了便于分析三相并网逆变器的单周期控制，将三相逆变器在六个区间内等效为双并联Buck型逆变器，三相并网逆变器六个区间划分如图5-37所示。六段区间的划分可以通过过零检测的方法实现，每相电压的过零点处为一个区间划分点。

在区间Ⅰ（0～60°）内，u_a＞0，u_b＜0，u_c＞0，开关管VT₆在整个区间内一直导通，控制另外两个开关管VT₁和VT₅来使平均电流i_a和i_c分别跟踪电压u_a和u_c，VT₂、VT₃和VT₄一直关断。即在每一时刻，只有两个开关动作，这就大大降低了开关损耗。由于三相电压的对称性，电流i_b自动跟踪电压u_b。由此得到单位功率因数。忽略交流侧电阻，逆变器在此区间等效为双并联Buck逆变器的拓扑结构如图5-38所示。

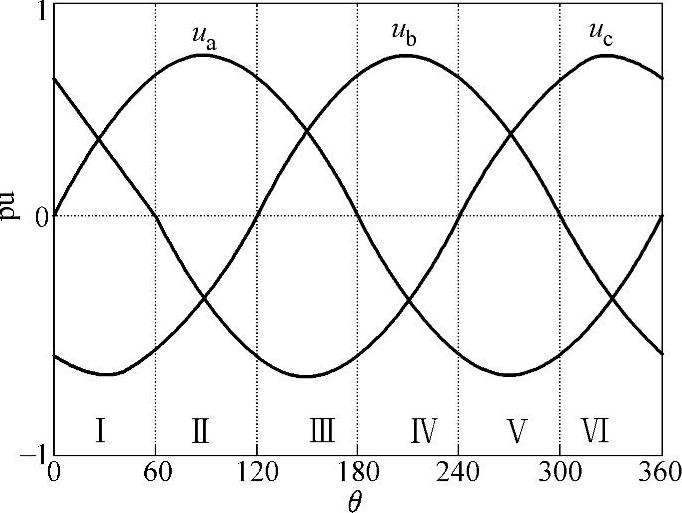
图5-37 三相正弦电压一个周期内的六个区间

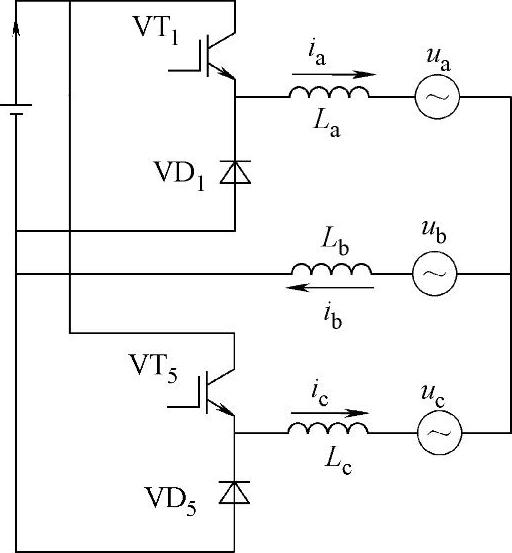
图5-38 区间Ⅰ的等效双并联Buck逆变器结构

变换器工作在恒定开关频率下，VT₁和VT₅有四种开关状态，如图5-39所示。而在一个开关周期内，仅存在两种开关次序，如图5-39a、5-39b、5-39d或图5-39a、5-39c、5-39d所示。由于开关频率远大于工频频率，可以由图5-38得到

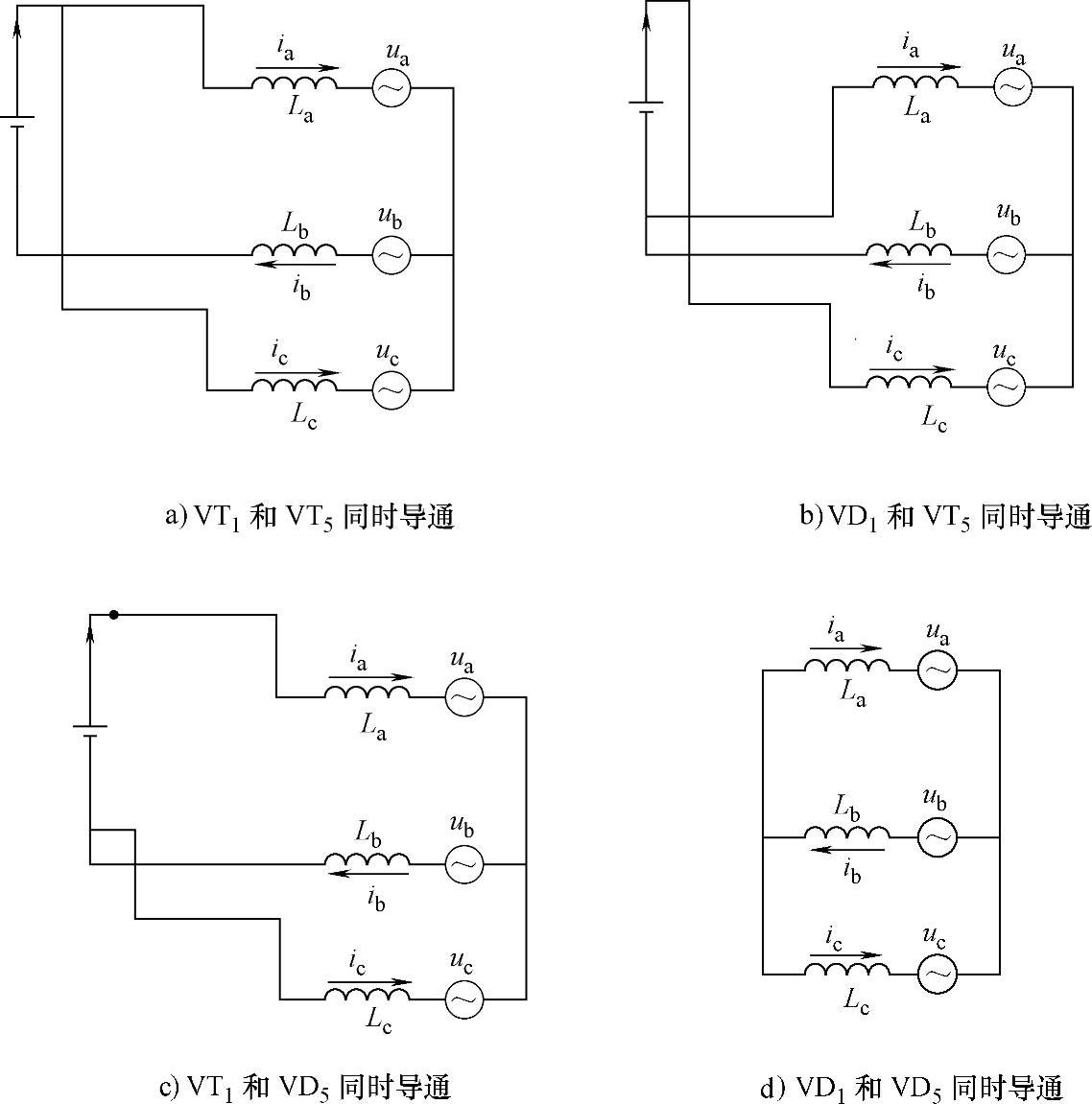
图5-39 区间Ⅰ四种开关模式

以单位功率因数运行，则输出的电流与电网电压同频同相，则有

考虑到交流侧电阻R_s，由（5-119）可得

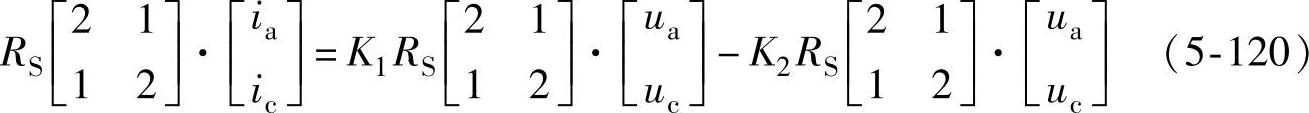
把式（5-118）代入式（5-120），并定义K=K₁R_S，U_m=K₂R_SE则可得

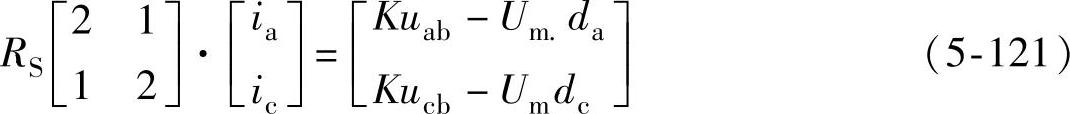
式（5-121）即为区间Ⅰ（0～60°）的单周控制模型，式中K和U_m将控制输出电流的大小。

同理，其余五个区间的等效电路与控制模型很容易推导，电压空间矢量区间划分电路将三相电压按照图5-37的方式划分为六个区间并生成区间选择信号，作为电流选择电路。电压选择电路和输出模块的选择信号，每个区间对应的参数见表5-4。具体使用时，只要用对应区间的u₁、u₂替换u_ab、u_cb，i₁、i₂替换i_a、i_c即可。

表5-4 各区间控制参数及开关表

完整的单周期控制三相并网逆变器的控制框图如图5-40所示。此控制器可以分为三个部分：①电网电压与其对应的输出电流的选择，得到u₁，u₂，i₁，i₂；②控制核心——单周控制电路，包括加法器、比较器、可复位积分器和触发器等；③输出驱动信号选择电路。

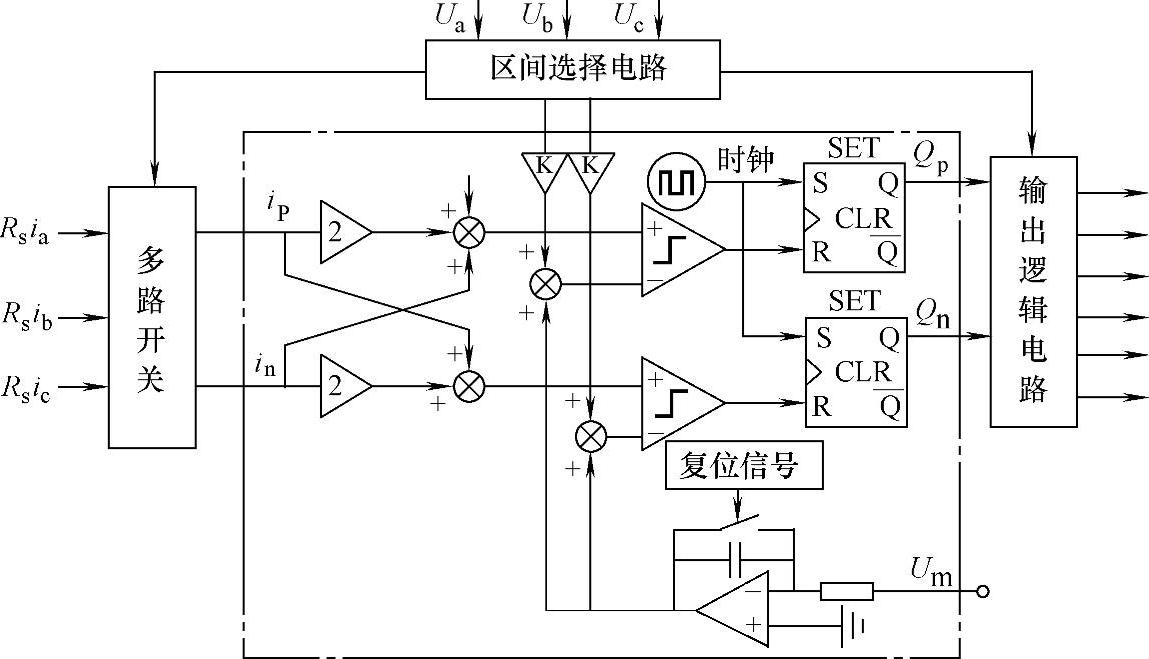
图5-40 三相并网逆变器单周期控制框图

5.4.4.3 变结构控制

变结构控制是一种非线性控制策略，广泛应用于各种控制系统中。变结构控制的非线性表现为控制的不连续性，而且在控制过程中不断地改变。变结构控制的通常法则是：每当系统相空间中的运动点穿越某些曲面（超曲面）时，就改变系统的结构。而这些曲面的形状本质上取决于控制对象的类型。对于电力电子变换器而言，每种开关状态的组合对应着不同的电路结构，开关动作就是从某一种电路结构到另一种电路结构的穿越。这与变结构控制的基本法则非常相似，因此变结构控制非常适用于电力电子变换器。变结构控制中最常用的是滑模控制，以下先介绍滑模控制的基本原理，再介绍其在并网逆变器中的应用。

1.滑模控制原理

（1）滑模控制的基本问题

设某一系统为

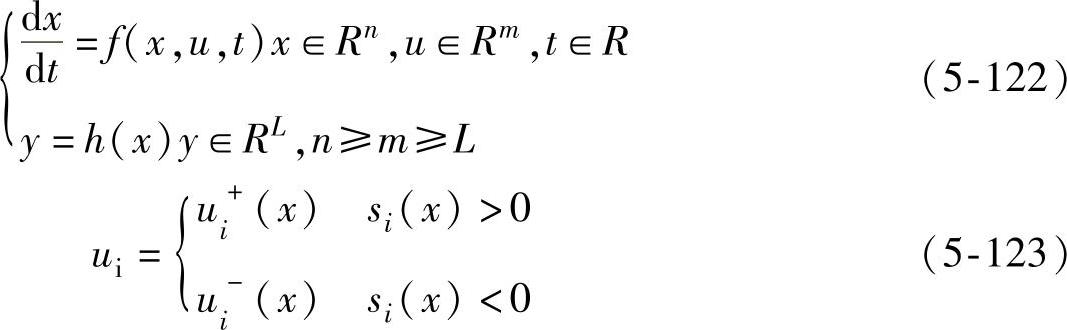
式中，u_i+（x）≠u_i-（x）（i=1，2，……，m），这也使得：

1）滑动模态存在；

2）满足可到达性条件：在切换面s_i（x）=0以外的状态点都将于有限的时间内达到切面；

3）滑模运动的稳定性良好；

4）变结构的运动品质良好。

以上前三项是滑模变结构的三个基本问题。满足这三个条件的控制就是滑模变结构控制，简称滑模控制，实现这种控制策略的控制算法通称为滑模控制器。

（2）滑模控制的基本策略

滑模控制有以下集中基本控制策略：

1）常值切换控制

2）函数切换控制

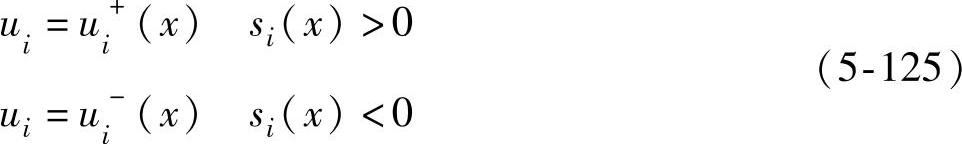
3）比例切换控制

式中，α_ij和β_ij是实数。

2.滑模控制的动态品质

滑模控制的运动由两部分组成：第一部分是系统在连续控制的正常运动，在状态空间中运动轨迹全部位于切换面以外，或者有限地穿越切换面；第二部分是系统在切换面附近沿切换面滑模运动。按变结构控制原理，正常运动段必须满足滑动模态的可达性条件。为了改善这段运动的动态品质，在一定程度上，可以用规定“趋近率”的办法加以控制。在广义滑模条件下，根据需要规定如下一些趋近率：

1）等速趋近率(www.xing528.com)

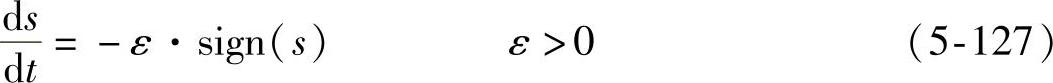
2）指数趋近率

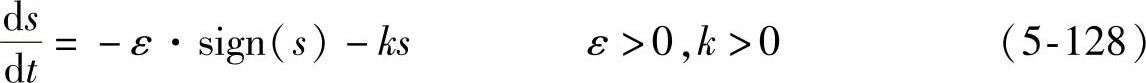
3）幂次趋近率

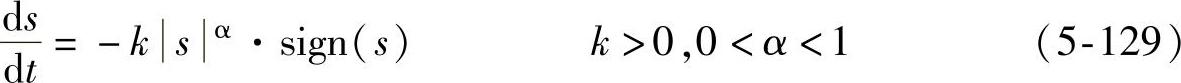
4）一般趋近率

在滑模运动段，实际上也由两部分构成：一部分是系统运动点在切换面附近上下穿行，该部分运动的产生使切换开关具有时间或者空间滞后；另一部分是系统沿滑动模态的极限运动。

3.滑模控制在三相并网逆变器电流控制中的应用

三相电压型并网逆变器的结构如图5-21所示。前面已经得到其在两相旋转坐标系下的数学模型为

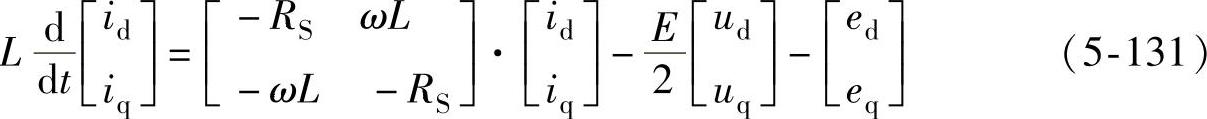
在线性控制方法中，需要对式（5-132）进行线性化处理。在滑模控制中，则可以直接构造滑模控制器，构造方法如下。

考虑引入电流状态反馈（ωLi_q和ωLi_d）进行系统解耦；而引入电网电压（e_d、e_q）作前馈补偿，令

将式（5-132）代入式（5-131），有

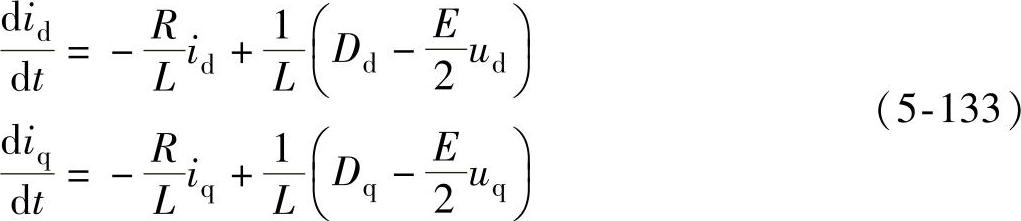
定义电流误差为

电流指令可看作常量，于是有

对电流误差列状态方程，有

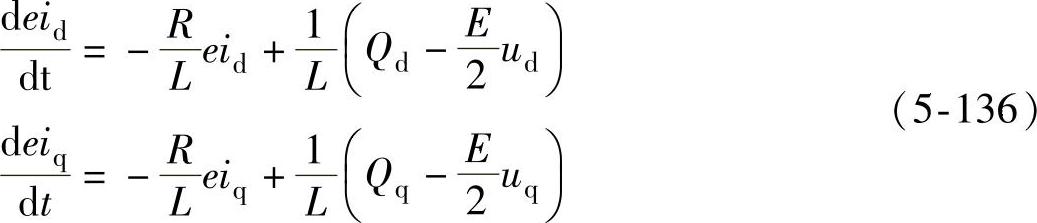
式中

式（5-133）中可以将D_d，D_q看成是扰动项，因此可以设计一个控制量来减弱此扰动项的影响。可以设计一个滑模控制器来处理D_d，D_q的扰动。提出的滑模控制器如下：

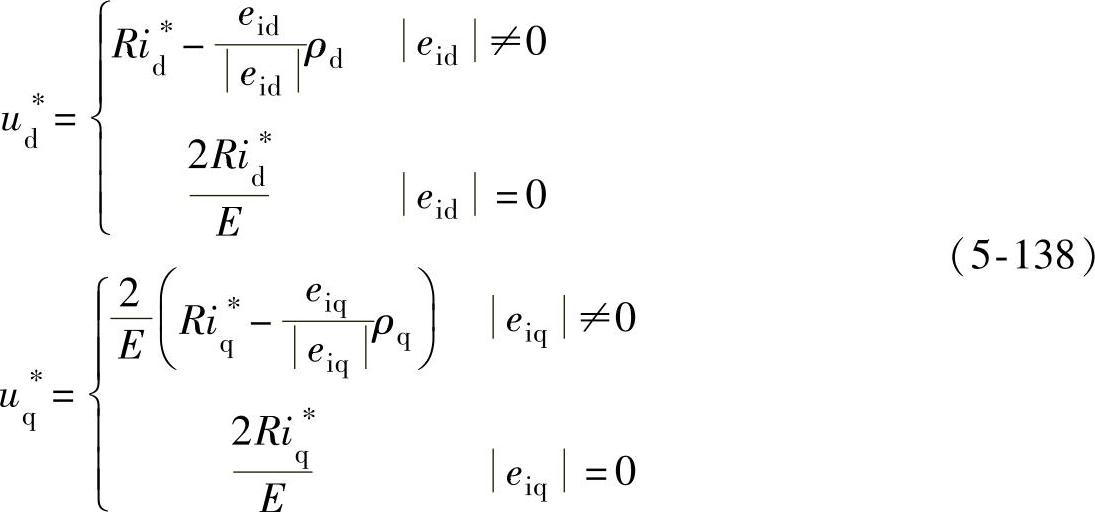
式中，ρ_d、ρ_q定义成D_d、D_q的最大值。

在实际控制过程中，根据实际的物理量，给出相应的式（5-137）的控制量，即可实现电流的变结构控制。

5.4.4.4 李亚普诺夫函数法控制

李亚普诺夫函数法控制是非线性控制理论中的一种控制方法，将其应用于光伏并网逆变器中，可直接实现非线性控制，且具有良好的动态性能，同时还可实现光伏阵列的最大功率点跟踪控制。

1.非线性数学模型

三相光伏并网的拓扑结构如图5-21所示。由于光伏阵列的直流电压往往随环境条件波动，因此将直流侧电压和交流侧电流一并作为被控对象进行控制。直流侧电压的三相并网逆变器在两相旋转坐标系下的数学模型可表示为

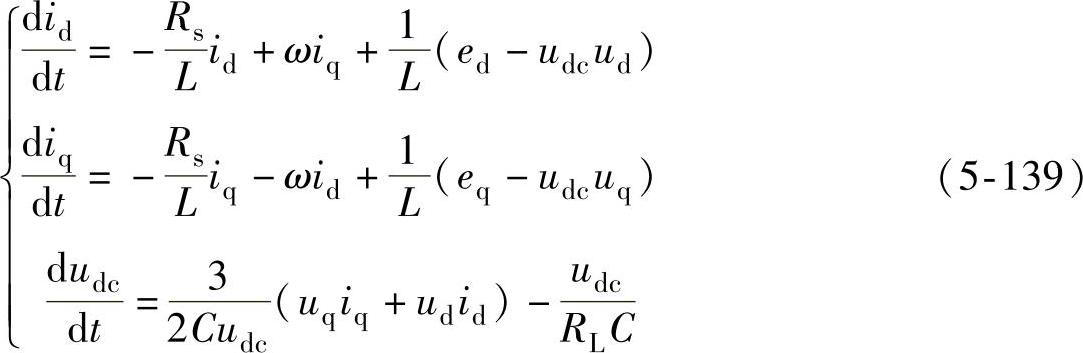
式中，u_dc为直流电压瞬时值；C为直流侧电容值；R_L为光伏阵列等效输出阻抗。

上面的方程组表示的系统为多输入多输出的非线性系统。为了方便对系统进行分析，将此系统写成如下的状态矩阵形式：

式中，X=（x₁，x₂，x₃）^T；U=（u₁，u₂）^T；f（X）=[f₁（X），f₂（X），f₃（X）]^T；

对比式（5-139），可知

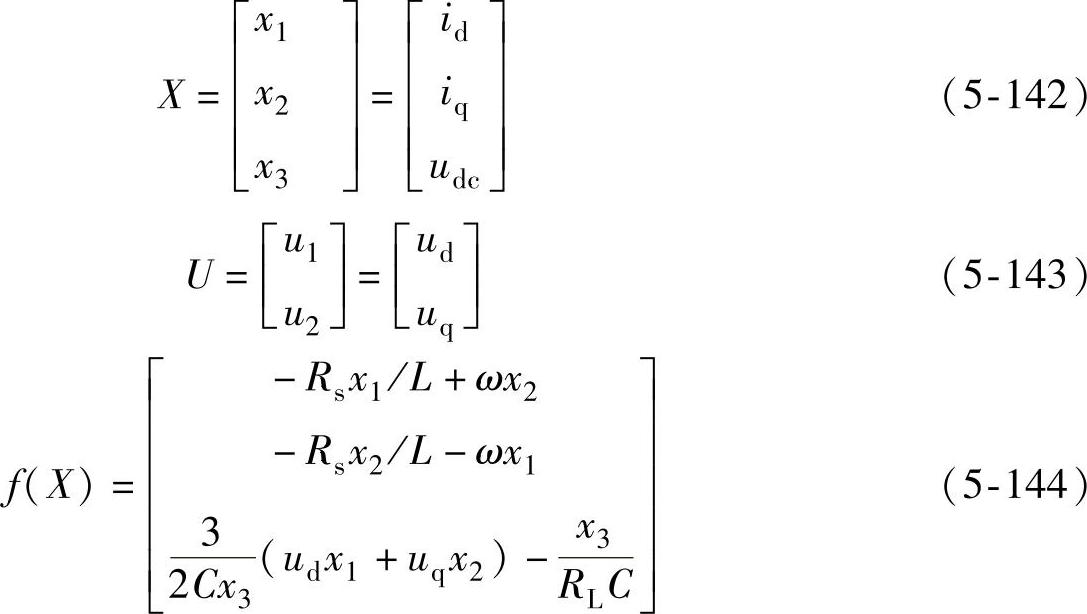
式（5-142）就是光伏并网逆变器的非线性数学模型。

2.控制李亚普诺夫函数法的原理

对于非线性自治系统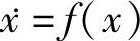，根据非线性系统理论，有下面的定理。

定理1：设集合x=0是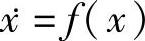的一个平衡点，V∶Rⁿ→R是一个连续一致可微函数，并满足

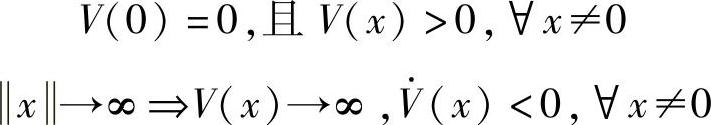
那么，x=0是全局渐进稳定的平衡点。

定理2：设集合x=0是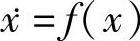的平衡点，并假定f是满足局部Lipschitz条件的，V（x）是一连续可微，正定，径无界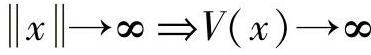（）的函数，若

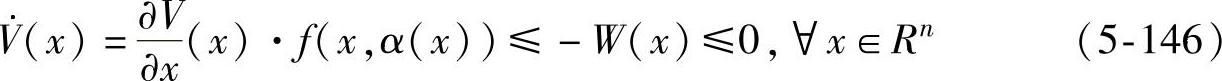
式中，W（x）是一个连续函数。那么方程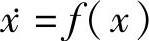的所有解都是全局渐进稳定的。另外，若W（x）是正定的，那么x=0是全局渐进稳定的。

那么对于非线性系统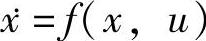，其中x∈Rⁿ，u∈R，可设计一个反馈控制率u=α（x），使闭环系统

在平衡点x=0处全局渐进稳定。

从以上分析和定理2可以看出，只要选择一个合适的控制李亚普诺夫函数V（x），并使它沿着式（5-147）的轨迹，满足即可。其中，W（x）是正定的。

3.光伏并网逆变器的非线性控制设计

由于并网逆变器的控制目标是将网侧电流正弦化，且为单位功率因数。因而并网逆变器与电网之间没有无功功率交换，控制时主要的控制目标是控制系统的线电流和电容电压，于是可以得到下面的输出方程

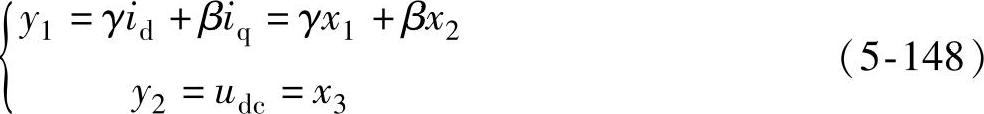
由于控制时为了使u_dc跟随指令值E（由MPPT算法获得），且使得电网获得单位功率因数，也即无功功率Q=0或i_q=0，从而上式可选择γ=0，β=1，以实现对i_q的控制。由输出方程及以上分析可以看出，（0，E）为（i_q，u_dc）的期望工作点，控制器的设计目标也就是将（0，E）作为（i_q，u_dc）的工作点。在模型式（5-140）的分析中发现，平衡点处，X=0，即i_d=i_q=u_dc=0，这显然是实际系统所不允许的。于是，考虑用坐标变换的方法将系统的期望工作点（i_d，0，E）变换为新系统的全局渐近稳定平衡点（0，0，0），并通过对x₁的控制实现对x₃的控制，使新的系统满足定理2中所要求的全局渐近稳定的条件。据此，为了找出合适的控制李亚普诺夫函数，先做如下的变换。

设α（E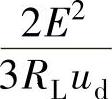）=，令z₁=x₁-α（E），z₂=x₂，z₃=x₃-E，代入式（5-140），可得到与原系统等价的新系统，为

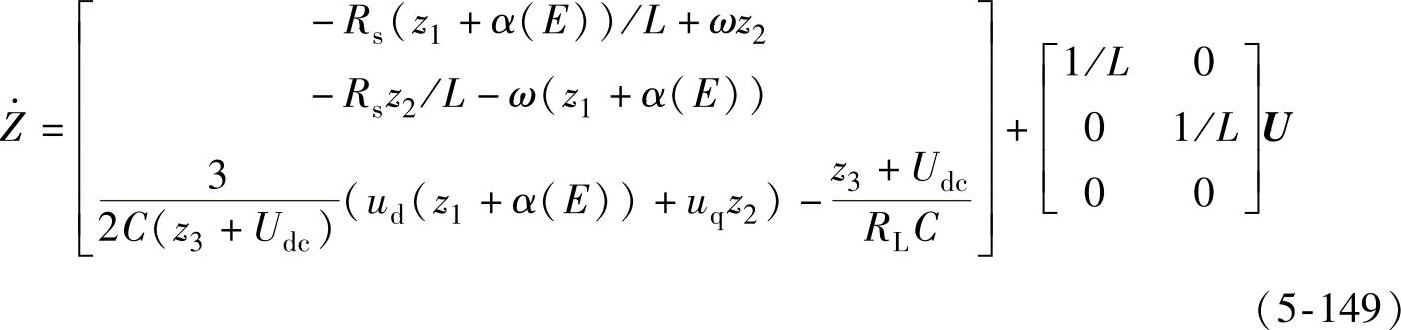
根据式（5-149），应用定理2，原问题就转化为求适当的控制输入的问题。使式（5-149）全局渐近稳定于原点，也就实现了对无功电流的控制和对最大功率点的跟踪。

下面根据定理2，利用控制李亚普诺夫函数V（z）来确定控制率U。取V（z）=（z²₁+z²₂+z²₃）/2，则有

将式（5-149）中的z₁、z₂、z₃代入式（5-150），化简可得

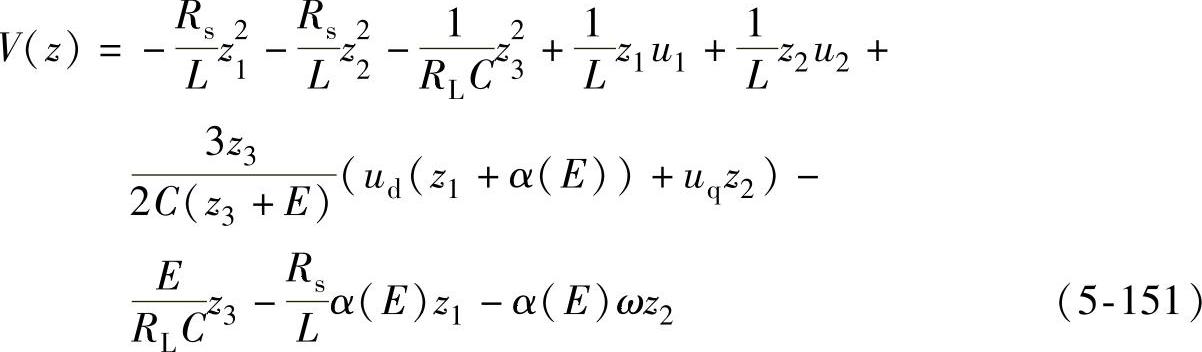
要使V（z）负定，只需令后六项之和为0，即

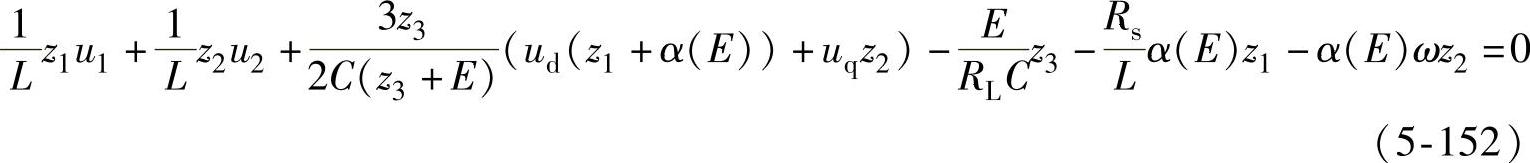
移项，整理得

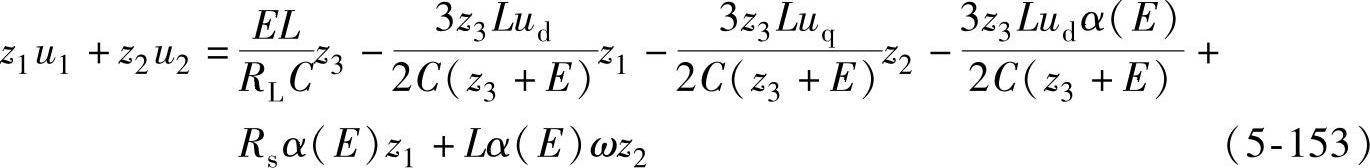
令

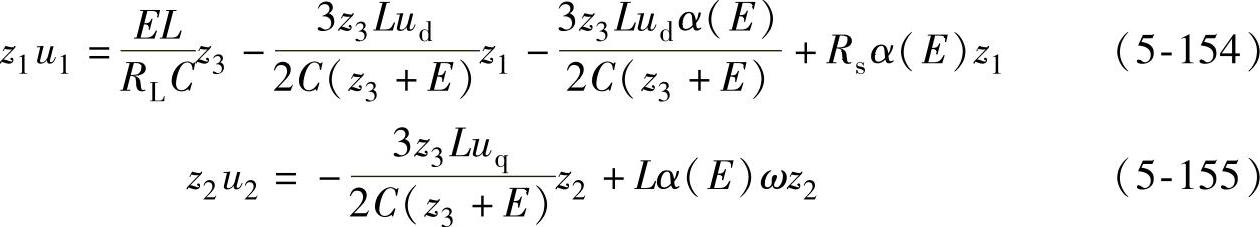
则可得控制率为

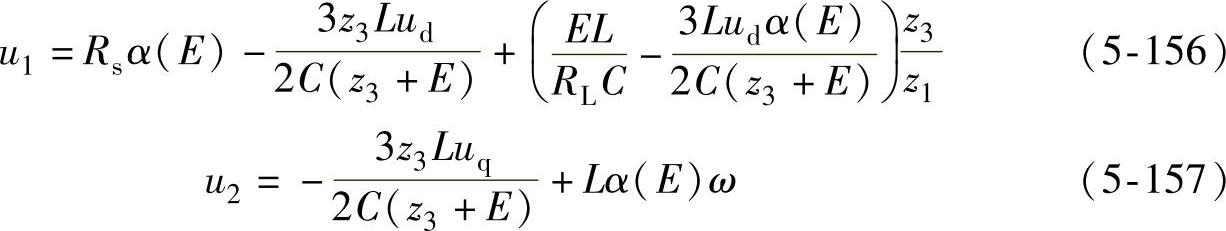
将式（5-156）、式（5-157）代入式（5-143），即可得控制率U。

由于参数R_s、L、R_L和C都是正数，因此设计出的控制率U可以满足定理2的要求，在平衡点z=0处全局渐进稳定。

系统控制框图如图5-41所示。

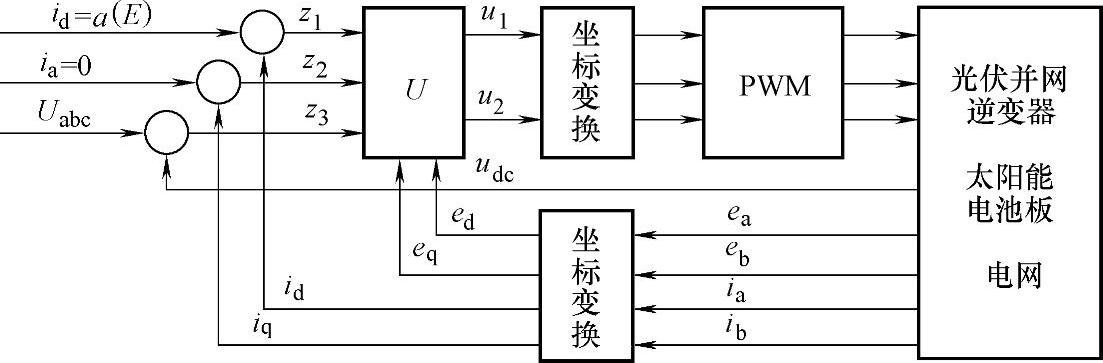
图5-41 光伏并网逆变器非线性控制框图