坐标变换法线性控制优化

逆变器的坐标变换法线性控制来源于三相电机的矢量控制，现在已经扩展到常规应用的三相变流器中。对于单相逆变器，也可以构造伪坐标系，实现坐标变换法线性控制。

5.4.2.1 三相并网逆变器的数学模型

三相并网逆变器的典型拓扑结构如图5-21所示。图中采用的是三相电压型桥式并网逆变器，滤波器为单电感滤波器，三相电感均为L，R是线路电阻，e_a、e_b和e_c是三相交流电源，i_a、i_b和i_c是三相并网电流，E为直流电源，N为直流侧虚拟中点，O为交流侧中点。对于其他形式的拓扑结构，以下的分析只需进行拓扑方面的相应改变即可，基本原理相同。

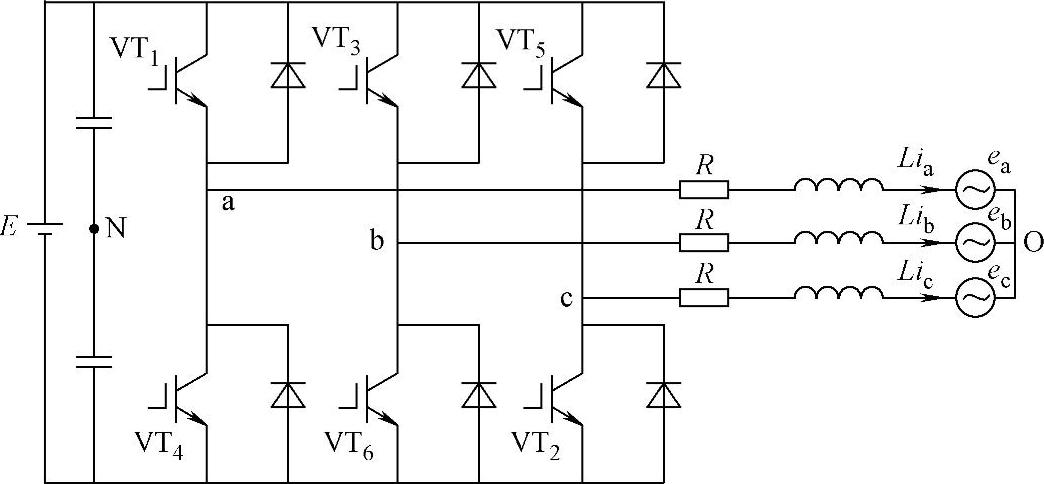
图5-21 三相电压型桥式并网逆变器拓扑结构

由图5-21，可得到三相电感的回路方程为

同时

在三相三线系统中，三相电流之和为零，所以有

i_a+i_b+i_c=0 （5-73）

在三相电网电压对称的条件下有

e_a+e_b+e_c=0 （5-74）

将式（5-73）和式（5-74）代入式（5-71），化简得

u_ao+u_bo+u_co=0 （5-75）

将式（5-75）代入（5-72），得

设逆变器的三相调制信号为u_ma、u_mb和u_mc，根据三相双极性SPWM原理，必有

u_ma+u_mb+u_mc=0 （5-77）

如果忽略u_aN、u_bN和u_cN的中高频谐波成分，只考虑基波，有

式中，E/2是对于SPWM而言的，对于SVM则应为。

综合考虑式（5-71）、式（5-72）、式（5-76）、式（5-77）和式（5-78），有

式（5-79）就是三相静止坐标系下三相并网逆变器的数学模型。可见，在三相静止坐标系下，三相之间是相互解耦的。

为了简化控制，引入三相静止坐标系到两相静止坐标系的变换关系式如下：

其逆变换为

将式（5-79）按式（5-80）进行代换，整理得到两相静止坐标系下三相并网逆变器的数学模型为

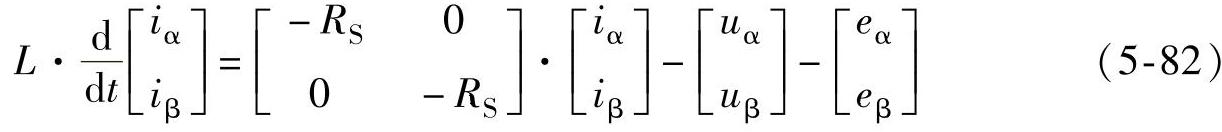
可见，在两相静止坐标系下，两相之间仍然是相互解耦的。

通过坐标转换，可得到两相旋转坐标系下三相并网逆变器的数学模型。从两相静止坐标系到两相旋转坐标系的变换关系式为

将式（5-80）代入式（5-83），可得从三相静止坐标系到两相旋转坐标系的变换关系式，为(www.xing528.com)

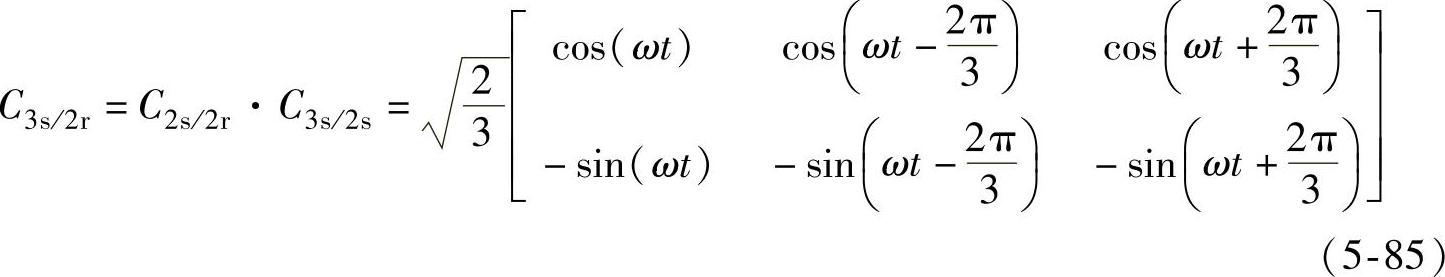
将式（5-83）代入式（5-82），整理得到两相旋转坐标系下三相并网逆变器的数学模型为

但需要注意的是，在静止坐标系相互解耦的状态方程经过坐标旋转变换后就相互耦合了。

式（5-86）表明，三相并网逆变器是一个多变量输入非线性强耦合的系统，必须对其进行线性化，才能使用线性控制理论的方法对其进行控制。常用的线性化方法是小信号模型分析法。

先定义如下：

式中，i_d0、i_q0、u_d0和u_q0为系统在稳定工作点的稳态量；Δi_d、Δi_q、Δu_d和Δu_q为稳态工作点附近的扰动量。

将式（5-87）代入式（5-86），分离稳态量和扰动量（小信号量），忽略高频分量，并假设交流电源电压为恒定量，可得到系统的小信号模型为

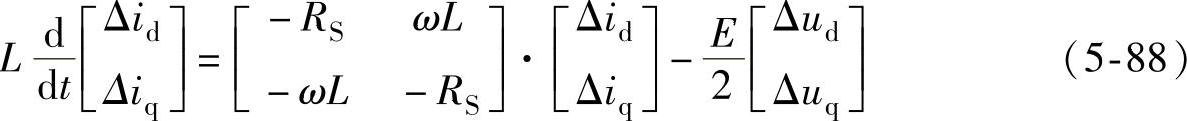
式（5-88）已经成为线性系统，其中所有的变量也都转化为直流量。因此可用常规的PI控制对系统进行控制。式（5-88）中的控制量为增量Δu_d和Δu_q，在实际控制中应根据式（5-87）转化为绝对量。

5.4.2.2 非解耦电流控制

前面谈到并网逆变器的控制有电流型和电压型两种，不论哪种类型都需要对逆变器的电流进行闭环控制。电流型控制不必多讲，电压型控制中也必须加入电流内环以增强系统的快速性和抗干扰性。

从式（5-86）可以看出，两个电流分量i_d和i_q相互有耦合关系。如果忽略掉这个耦合关系（考虑到耦合关系可视为前向通道上的干扰，这种忽略在一定程度是可以的），则逆变器的传递函数可简化为由电感L和线路电阻R构成的一阶惯性环节。

设计过程中，因为d轴、q轴的结构完全相同，可以采用相同类型的调节器，电流环在突加控制作用时不希望有超调量，或者希望超调量越小越好，从这个观点出发，应该把电流环设计成典型的I型系统。电流环还有对输入电压波动及时调节的作用，为了提高其抗扰动性能，也可以把电流环设计成为典型的II型系统。对于变流器而言开关频率和电流采样频率较高，典型I系统的抗扰恢复时间可以接受，下边按照典型I型系统设计电流环。电流环控制系统结构如图5-22所示。图中，T_oi为电流反馈滤波时间常数，T_s为电流内环采样周期。为了进一步简化调节器设计和抑制电流超调，增加了滤波环节。

图5-22 电流环控制系统结构

不考虑输出电压影响时，忽略开关导通电压降，选择阻尼系数ζ=0.707，此时动态响应应略有超调。为了让调节器零点抵消掉控制对象大时间常数极点，得到PI调节器的积分时间常数τ为

根据最优工程设计法，比例系数k_p与小时间常数的关系为

式中，T_∑i=T_oi+T_s，为小时间常数之和。

于是调节器比例系数为

5.4.2.3 前馈解耦电流控制

前馈解耦电流控制的控制框图如图5-23所示，其中忽略了小时间常数。

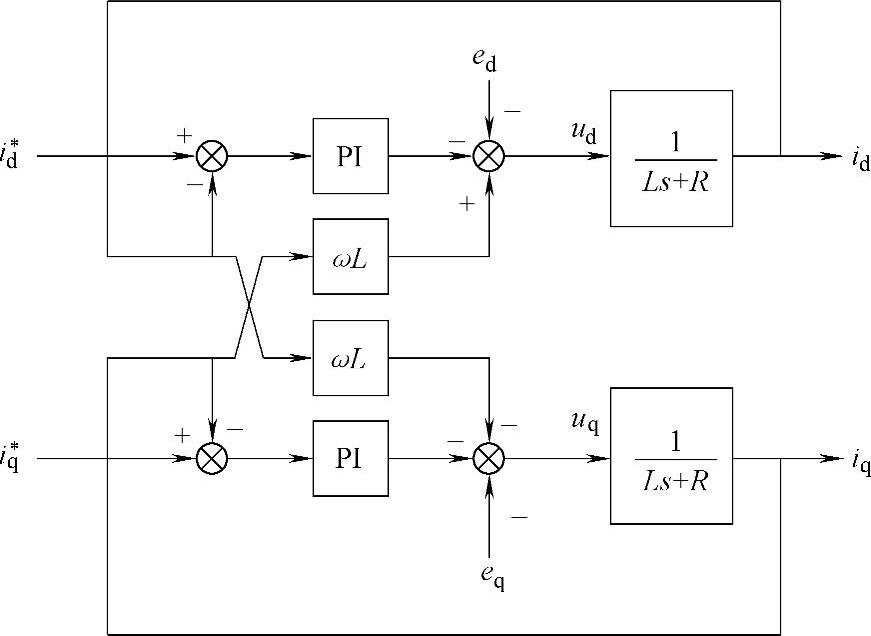
图5-23 前馈解耦电流控制框图

图中控制量u_d和u_q分别为

该控制因考虑了反电动势与耦合电流扰动项，因此动态性能优于非解耦控制。对于解耦性能，耦合项属于扰动量，闭环系统的抗干扰性能取决于调节器的设计。要想进一步提高系统性能，还需进行模型解耦，这里不多赘述。

5.4.2.4 单相并网逆变器的坐标变换控制

与三相系统实际存在的三相静止坐标系不同，单相系统并没有真正的静止坐标系。因此要想使单相系统也能采用类似三相系统的坐标变换控制，必须构造虚拟的伪静止坐标系。

单相系统伪静止坐标系的构成办法有多种。其中一种办法是通过移相构造出对称的三相电路，然后按照三相电路坐标变换的方法进行控制。这种办法存在的问题是需要增加单相到三相的相位延时变换环节，从单相到三相的变换至少需要60°的相位延时。因此实时性受影响。