当分布式发电系统要求并入电网的功率已知时,可以根据电网情况求出其期望电流或期望电压值,从而采用电流型控制并网模式或是电压型控制并网模式控制光伏逆变器,将能量并入电网。电流型控制并网模式对于并网运行的控制简单易行,如果不考虑传输线阻抗的影响,功率分析很简单。但电流型控制并网模式难以为常规本地负载进行独立供电,在公共电网故障状况下,如需为本地负载供电,则需转换至电压型控制并网模式,也就是存在模式切换问题。当采用电压型控制并网模式时,独立运行与并网运行可以工作于相同的控制模式,没有模式切换问题。本书着重介绍电压型并网控制模式,下面介绍其功率调节技术。
下垂控制是分布式并网控制中常用的方法。分布式发电系统中供电单元多,实现有功功率—频率的下垂特性,可以保证有功功率的分配和均衡。下垂特性应由总的功率分配及额定功率的大小而定。无功功率也应有类似的下垂特性,以保证无功功率的分配和均衡。这种下垂特性的实现分别是由频率及电压来控制的。
电压型控制并网模式的复频域等效电路如图5-10所示。该图为单相电路,但也适用于三相电路。图中电抗X和电阻R2为等效阻抗,包括滤波器电抗、变压器漏阻抗及线路阻抗等。
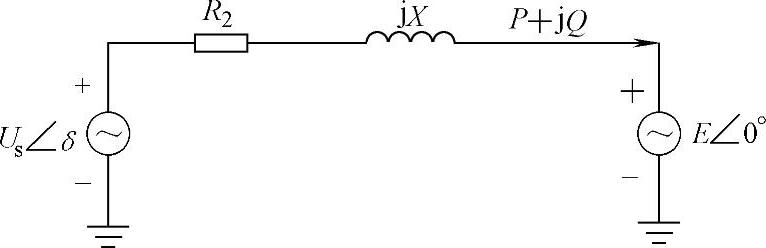
图5-10 电压型控制并网模式的复频域等效电路
根据图5-10,功率表达式可以描述为
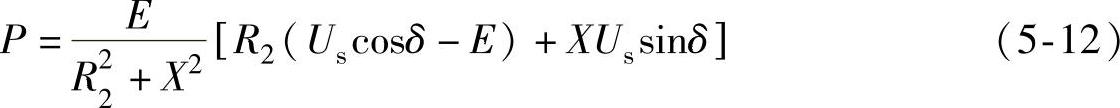
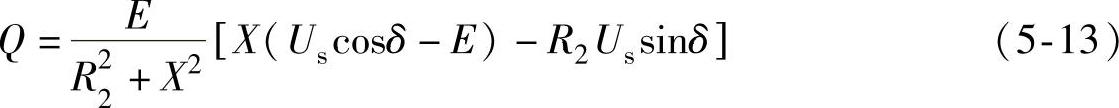
由式(5-12)和式(5-13)可解得
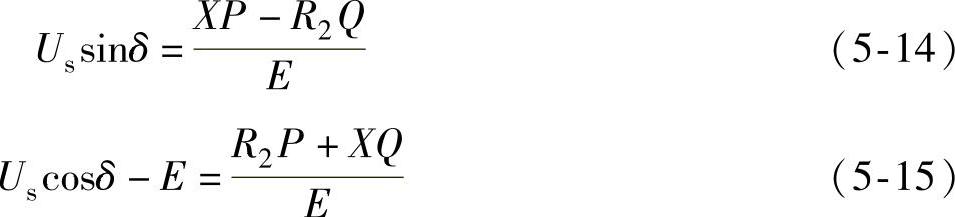
根据X与R2的相对关系,分为以下三种情况讨论。
1.X>>R2
这种情况意味着R2可以忽略。如果功率角δ很小,那么sinδ≈δ,cosδ≈1,则式(5-14)和式(5-15)可简化为

式(5-16)和式(5-17)表明,较小的功率角δ主要取决于有功功率P;电压差Us-E主要取决于无功功率Q。换一个角度说,可以通过单独调节功率角δ调节有功功率P,通过单独调节电压幅值调节无功功率Q。而功率角δ,本身又跟频率f有关,为角频率的积分,因此也可以通过调节频率f来调节功率角δ,进而调节有功功率P。以上叙述中关于调节有功功率P、无功功率Q的论述就是基于经典的频率、电压下垂控制策略。
下面给出经典的下垂控制策略为
f-f0=-kP(P-P0) (5-18)
Us-Us0=-kQ(Q-Q0) (5-19)
式中,f0和Us0分别是额定频率和额定逆变器输出电压(一般为电网电压);P0和Q0分别是额定的有功功率和无功功率。经典的频率和电压下垂控制特性如图5-11所示。
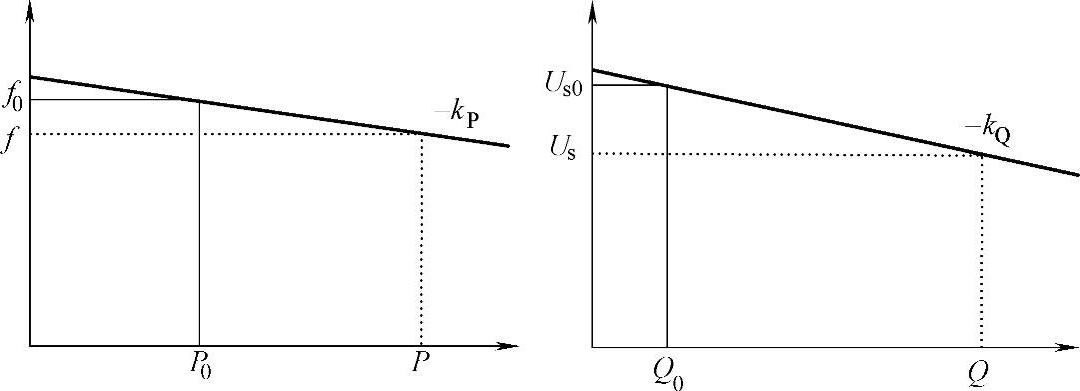
图5-11 经典的频率和电压下垂控制特性
2.X<<R2(https://www.xing528.com)
这种情况意味着X可以忽略。如果功率角δ很小,同样sinδ≈δ,cosδ=1,则式(5-14)和式(5-15)可简化为

式(5-20)和式(5-21)表明,较小的功率角δ主要取决于无功功率Q;电压差Us-E主要取决于有功功率P。可以通过单独调节功率角δ调节无功功率Q,也即可以通过调节频率f调节功率角δ进而调节无功功率Q,通过单独调节电压幅值调节有功功率P。在这里,经典的下垂控制策略已经不再适用了。
3.X与R2相接近
这种情况下,两者都不能忽略。这就需要找到在P、Q、Us、δ之间普遍存在的规律。一旦找到这一规律,将使得情况1和情况2在该规律中成为特例。为实现这一目标,这里引入了一个正交线性旋转变换矩阵T,将有功功率P和无功功率Q修正为P′和Q′,即
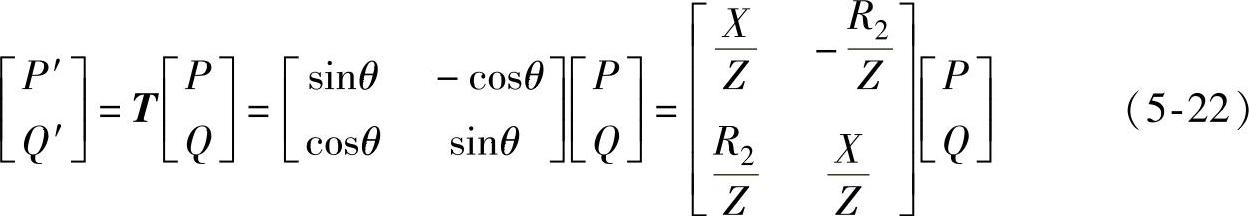
式中,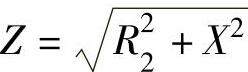 。
。
将式(5-22)代入式(5-14)和式(5-15)有

考虑到功率角δ很小,sinδ≈δ,cosδ≈1,则式(5-23)和式(5-24)可简化为

式(5-25)和式(5-26)表明,功率角δ主要取决于P′;电压差Us-E主要取决于Q′。可以通过单独调节功率角δ调节P′,通过单独调节电压幅值调节Q′。而功率角δ又是频率f的函数,因此也可以通过调节频率f来调节功率角δ,进而调节P′。
这里仿照经典的频率电压下垂控制策略的表达形式,给出了修正后的下垂控制策略(见图5-12):
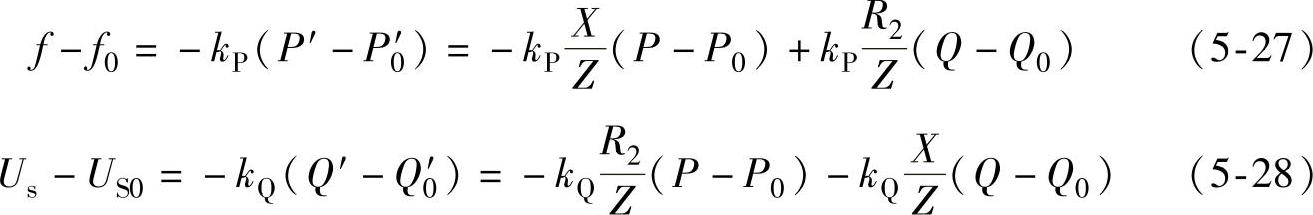
式中,kP、kQ分别指有功、无功下垂特性的斜率。
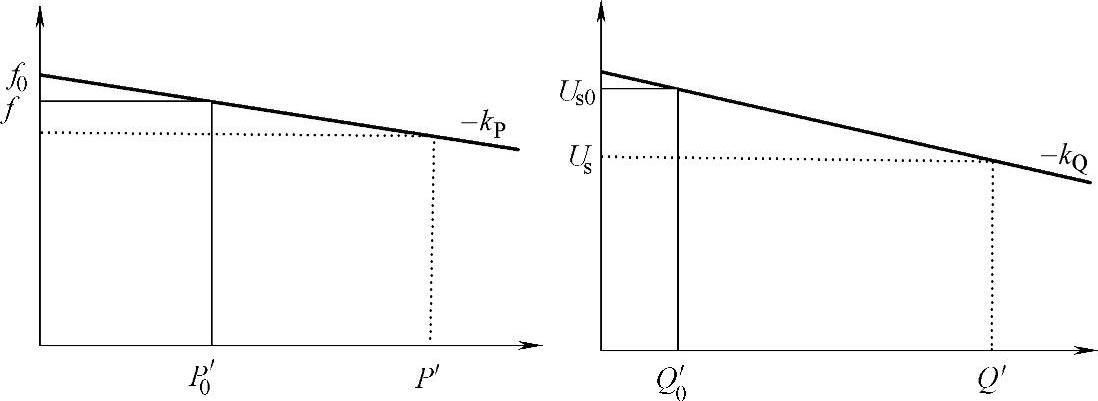
图5-12 修正后的频率和电压下垂特性
由于在分析中对线路阻抗R与X同时予以了考虑,因而这种情况更具有普遍意义。图5-13给出了不同线路阻抗构成下,P′、Q′、P和Q对于频率和电压的影响。
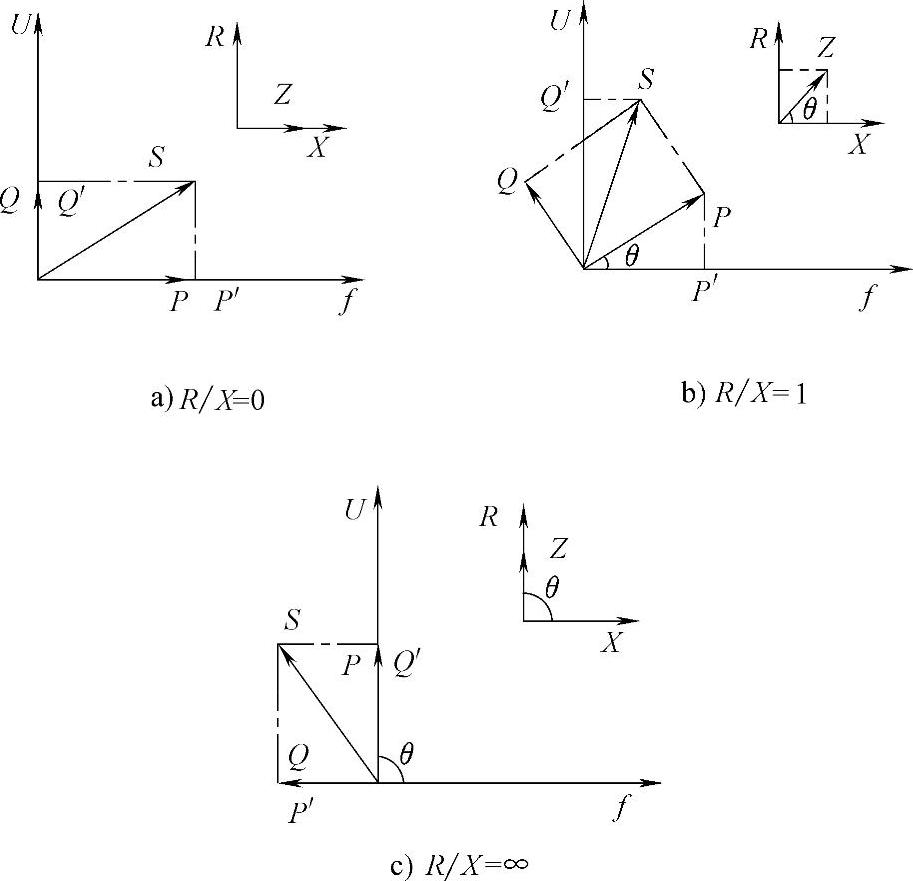
图5-13 不同线路阻抗构成下P′、Q′、P、Q对频率和电压的影响
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




