实现PID控制算法的程序优化

1.离散系统PID控制算法

图4-32表示了离散系统PID控制的算法框图。从图4-32可知，它的控制值P（n）是I、KE_n、D三部分的和。这里未计及偏差为零时的控制值M，但这可通过执行积分运算实现。图中M₂为干扰量，R₀为设定值，C为实际值，T为采样周期（PID运算间隔时间）。

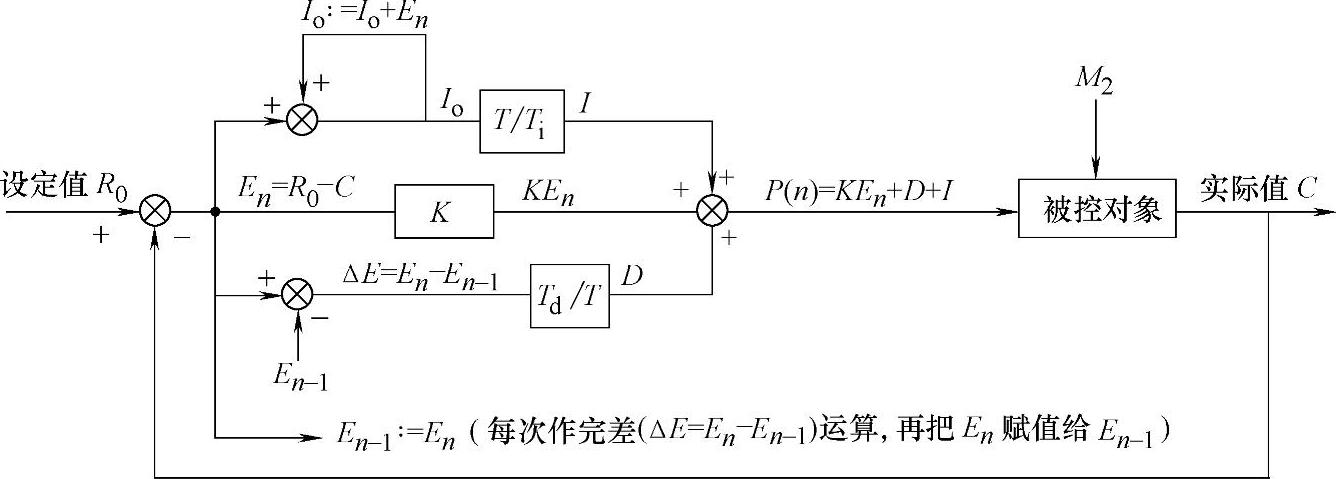
图4-32 PID控制的算法框图

2.离散系统PID控制梯形图程序

图4-33为与图4-32框图算法对应的一种梯形图。它用的是符号地址，较便于理解。

图4-33上标有18个注解，分别说明如下：

⓪对图4-33b，考虑到模拟量输入格式，把AW8（假设为模拟量输入字）的内容右移3位，并存于“实际值”中。对图4-33c读取模拟量输入值，并存于“实际值”中。

①图4-33a用定时器TIM001、图4-33b用定时器T101、图4-33c用定时器TI、实现每1s（此值可设）执行一次PID运算。这里1s即为采样周期T。

②求设定值与实际值之差。

③对图4-33a，如设定值比实际值小，则先求偏差的绝对值（因借位位也参与运算，故加1）。然后，用它去减积分值0。

④对图4-33a，如积分值0小于0，则其取值为0（最小值控制）。

⑤对图4-33a，如设定值比实际值大，则把偏差E_n加积分值0。

⑥对图4-33a，如加后积分值0超过9999，则其取值为9999（最大值控制）。对图4-33b，如加后积分值加后进位（SM1.1 ON），则其取值为32727（最大值控制）。对图4-33c，如加后积分值加后进位（M8022 ON），则其取值为32727（最大值控制）。

⑦积分值0除积分常数。

⑧求偏差的变化，保存原偏差值

⑨对图4-33a，如偏差为负变化，则求其补码。(www.xing528.com)

⑩偏差的变化乘微分常数。

⑾偏差值En与比例系数K相承，其积存于“KEn”。

⑿积分值与“KEn”偏差相加，其和存于“控制值”。而对图4-33a，如设定值比实际值大才作此相加。图4-33a，如加后有进位，即大于9999，则“控制值”取值为9999（最大值控制）。对图4-33b，如加后积分值加后进位（SM1.1 ON），则其取值为32727（最大值控制）。对图4-33c，如加后积分值加后进位（M8022 ON），则其取值为32727（最大值控制）。

⒀对图4-33a，如设定值比实际值大才作此相减。其后如需要也可作最小值控制。

⒁“微分值”与“控制值”相加，并存于“控制值”。而对图4-33a，如偏差正变化才作此相加。

⒂对图4-33a，如加后有进位，即大于9999，则“控制值”取值为9999（最大值控制）。对图4-33b，如加后积分值加后进位（SM1.1 ON），则其取值为32727（最大值控制）。对图4-33c，如加后积分值加后进位（M8022 ON），则其取值为32727（最大值控制）。

⒃对图4-33a，如偏差为负变化，则“控制值”与“微分值”相减，并存于“控制值”。

⒄如“控制值”小于0，则其取值为0（最小值控制）。

⒅把“控制值”转换为二进制数，并送通道13，即模拟量输出通道。对图4-33b，考虑到模拟量输出格式，把“控制值”又左移3位传QW10，即模拟量输出通道。对图4-33c，把“控制值”传模拟量输出模块的指定通道。到此才产生实际模拟量输出。

提示1：用一个字的BCD码表达一个数，其值可从0～9999，无法表达负数。当相减出现负值时，无法处理。为此，要做相应判断，好在欧姆龙PLC提供了用进位位（P-CY）可作判断。但还是相当麻烦。此外，BCD表达的数值范围也小。故最好用双字表达，运算指令也用双字长。特别是存储积分结果值的数据格式，尽量用双字长。这样，可提高控制精度，而且也便于PID参数整定。

提示2：用一个字带符号位的十六进制表达一个数，其值可从-32768～+32767，正、负数均可表达，也都可处理。图4-33b、c用的是带符号位的十六进制数，所以，程序简单多了。欧姆龙新型或稍高档的PLC也可用此码表达与处理。相反，西门子、三菱PLC则无法用BCD码对数值进行计算，它们用的都只能用十六进制。

图4-33 PID控制梯形图程序

提示3：为了可靠，对计算结果是否越界要进行控制。否则将得不到正确结果。

提示4：一般讲，当今PLC多有PID指令，直接使用它即可实现模拟量的PID控制。用户所要做的工作只是进行有关PID控制参数的设定。有的PLC，这些参数还可通过执行自整定（有的称调谐）命令自动获得，用起来就更方便了。