组合逻辑综合实例

1.三个开关表决逻辑

该3个开关分别用A、B、C表示。表决结果用灯L表示。每个开关也都有两个状态，即下扳（赞成）、上扳（不赞成）。下扳（通）用变量，即用A、B或C表示。上扳（断）用变量的非，即用A、B或C表示。

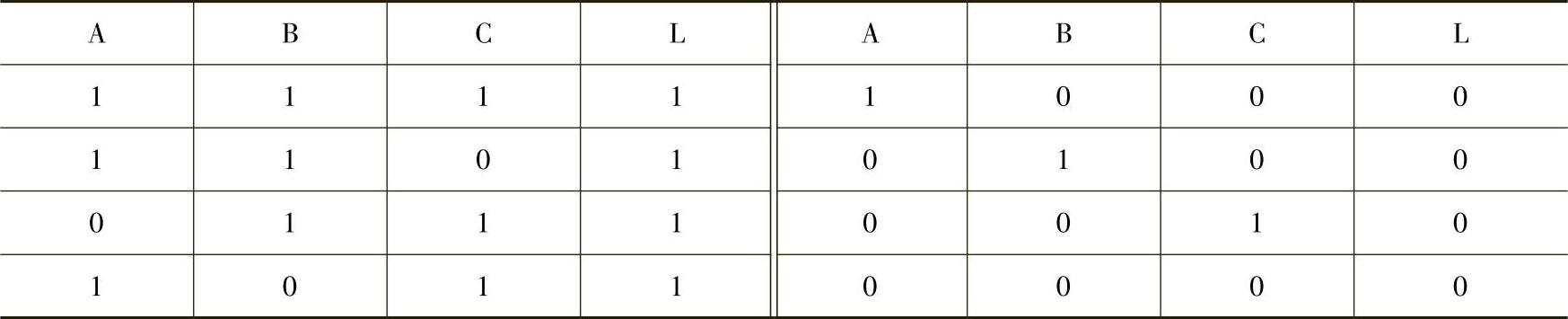
这3个变量各有两个取值，下扳的是两个及两个以上的有4种。把这4种组合使灯亮，即可实现所要求的控制了。对此分析，可用真值表表示，见表2-3。

表2-3 表决控制真值表

它的逻辑表达式应为

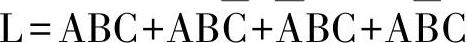
经化简则为

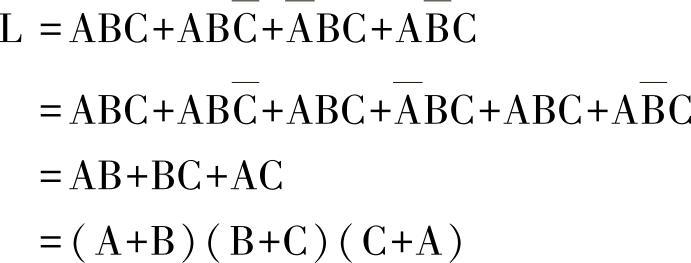
当然还应对这个表达式进行化简。不过由于使用PLC，触点多少问题不大，可直接依据此表达式画出的梯形图，如图2-4所示。图2-4a串联后并联。图2-4b为并联后串联。

这里仅用3个开关表决。如果多了，如几十、几百，就太复杂了。为此可用后面将要介绍的高级逻辑设计方法设计。

2.格雷码到二进制码译码

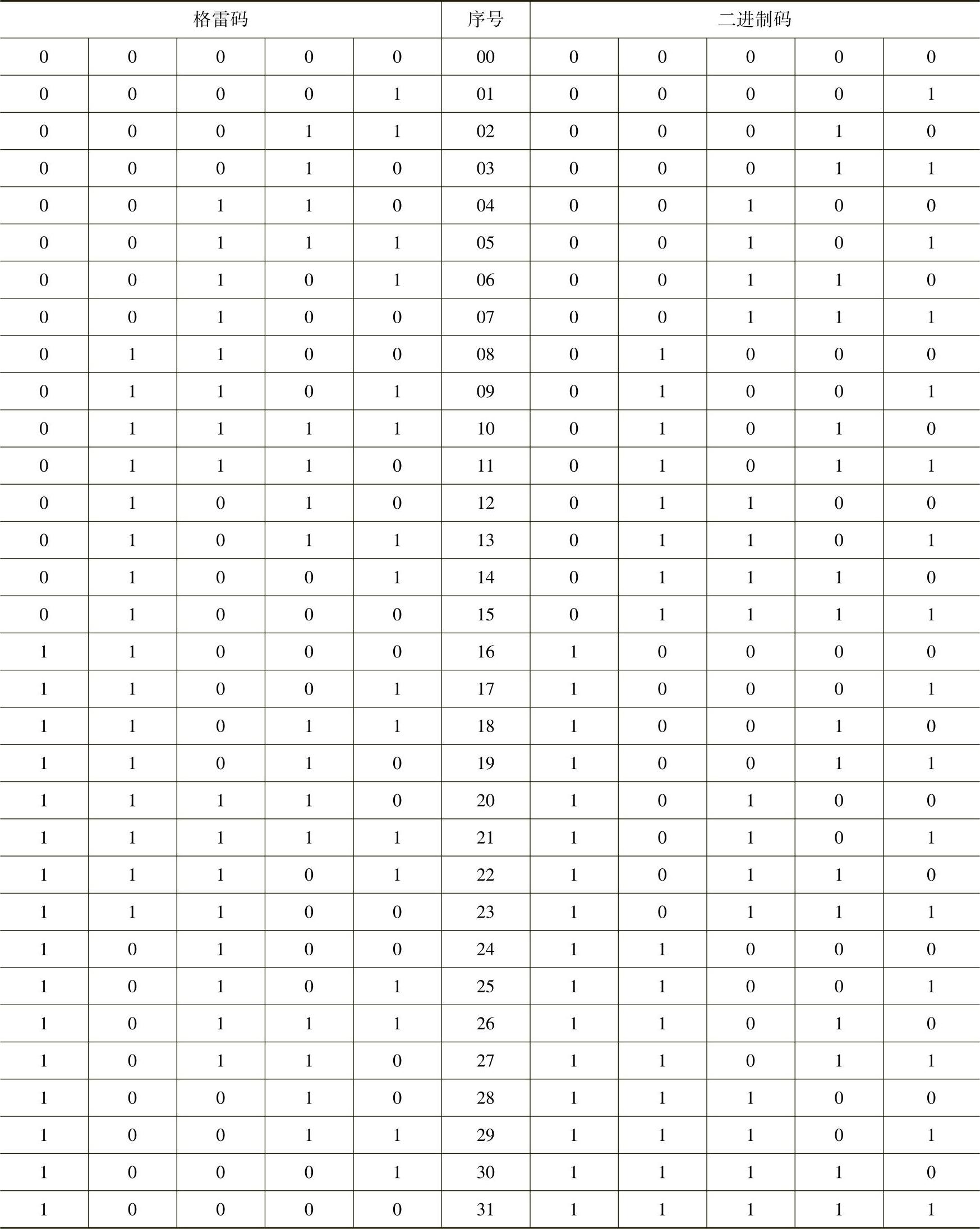
格雷码为单位码，不少绝对值计数的旋转编码器用它编码。但格雷码没有“权值”，无法用作大小比较。但它与二进制码有对应关系，其关系真值表见表2-4（5位）。以此关系，可把它译成二进制码。

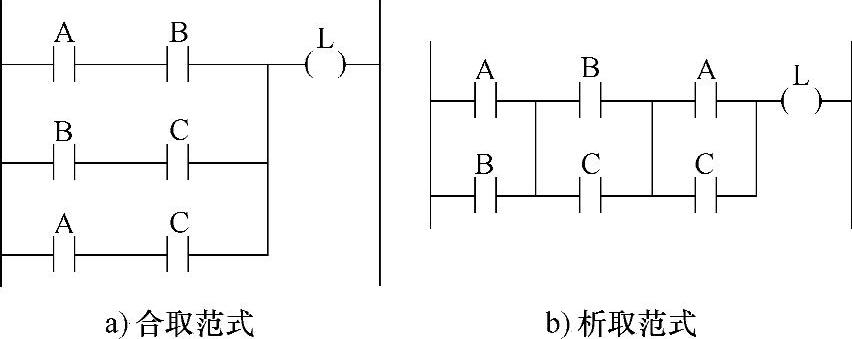
图2-4 三个开关表决电路

表2-4 二进制码与格雷码对照真值表

从表2-4可知，二进制码的本位的值为：格雷码的本位值与二进制码高一位值的异或，即(www.xing528.com)

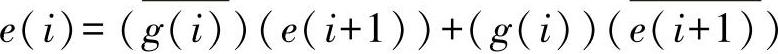
式中 e（i）——第i位二进制值；

g（i）——第i位格雷码值；

e（i+1）——第i+1位格雷码值。

而最高位两者相等。

图2-5即为此译码程序。该图g0（低位）～g4（高位）为格雷码，e0（低位）～e4（高位）二进制码。

图2-5程序设计的根据是表2-4。从表知，二进制码的本位的值为：“格雷码”的本位的值与二进制码的高一位的值的异或，即

e（i）=[g（i）xore（i+1）]

式中 e（i）——第i位二进制值；

g（i）——第i位“格雷码”值；

e（i+1）——第i+1位“格雷码”值；

xor——逻辑异或。

而最高位两者是相等的。

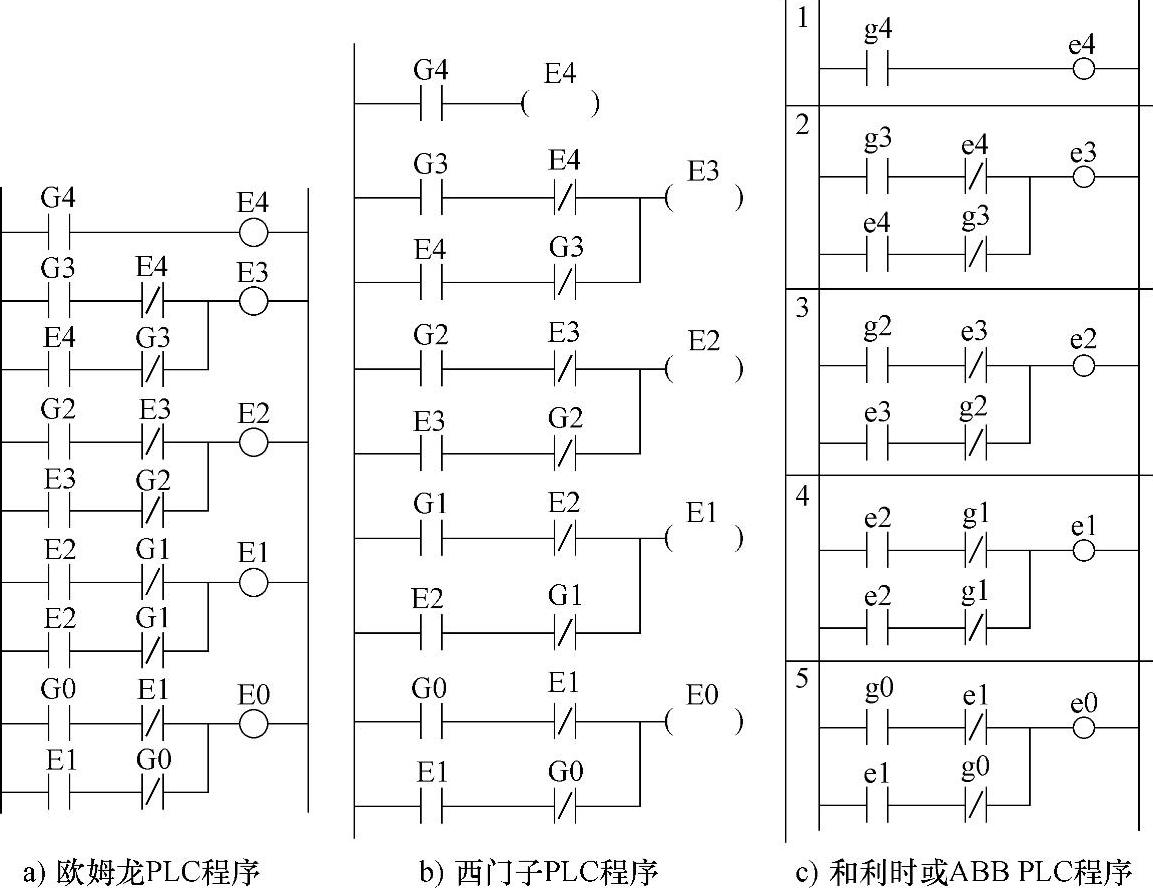
图2-5 格雷码到二进制译码程序

提示：当今，不少PLC提供有这两种编码的转换指令，不必调用这里介绍的转换程序。