计算螺钉受弯曲应力的强度

受拉、压应力的零件如果还受弯曲应力，则对于其强度有很不利的影响。这一节介绍受偏心载荷引起弯曲应力的螺钉强度计算，对这一问题的几种计算方法进行比较。也可对其他受弯曲零件的分析提供参考，准确的计算受弯曲零件的强度，减轻机器的重量。

下页介绍三种常用受偏心载荷螺栓的强度计算方法。

1.拉弯应力叠加法（图4-17）

外载荷F作用线偏离螺钉中心线距离为e，螺钉所受之拉弯合成应力σ_c为：

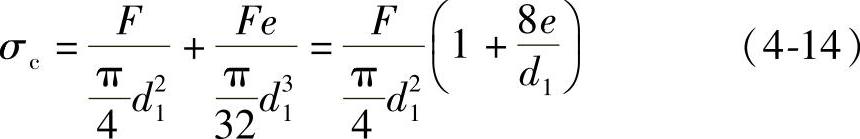
当e=d₁时，合成应力比单纯拉伸（e=0）时大8倍。应尽量避免螺钉受偏心载荷。这一方法对弯曲应力的影响，计算结果过大，与实际有差距。

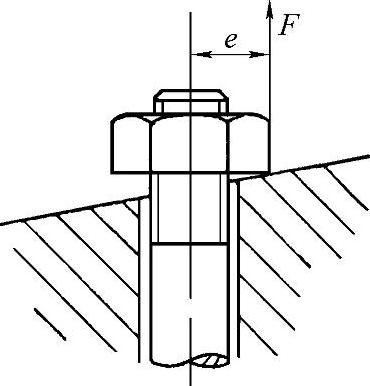
图4-17 受偏心载荷螺钉

2.按螺杆弯曲曲率计算弯曲应力

螺栓受拉伸应力σ及弯曲应力σ_w，可把螺杆弯曲的形状假设为半径为ρ的圆弧，其上端的转角为α，由此可得螺杆内的弯矩，按材料力学公式为M=EI/ρ，钉杆的弯曲应力σ_w=M/W，由图4-18根据几何关系ρ=l/α。式中l为钉杆长度。取W=πd³/32，I=πd⁴/64，则

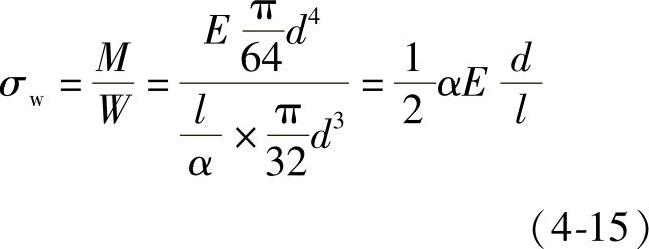
螺纹部分弯曲应力

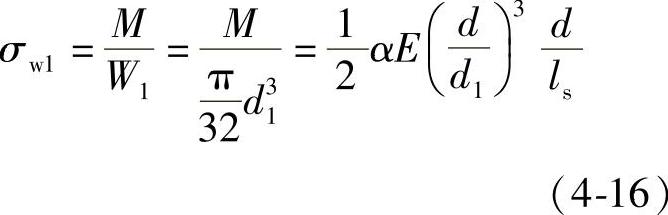
式中d ——钉杆直径；

d₁——螺纹内径。

式（4-15）、式（4-16）表明弯曲应力与头部转角、材料弹性模量、钉直径成正比，与钉长度成反比。这个结论比式（4-14）合理。例如，当α=0.5°，d=10mm，d₁=8.376mm，l_s=50mm，E=2×10⁵ MPa时，σ_w1=297MPa，此值也是不容忽视的。

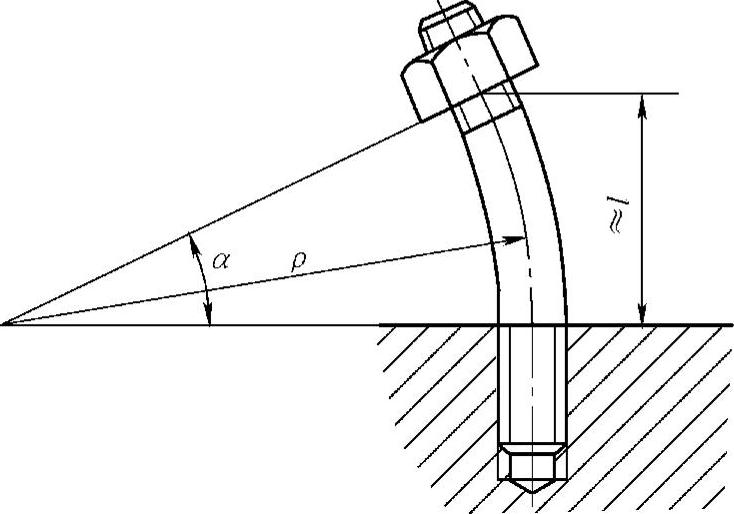
图4-18 支承面倾斜引起钉杆弯曲

3.考虑弯曲和拉伸的综合作用（图4-19）

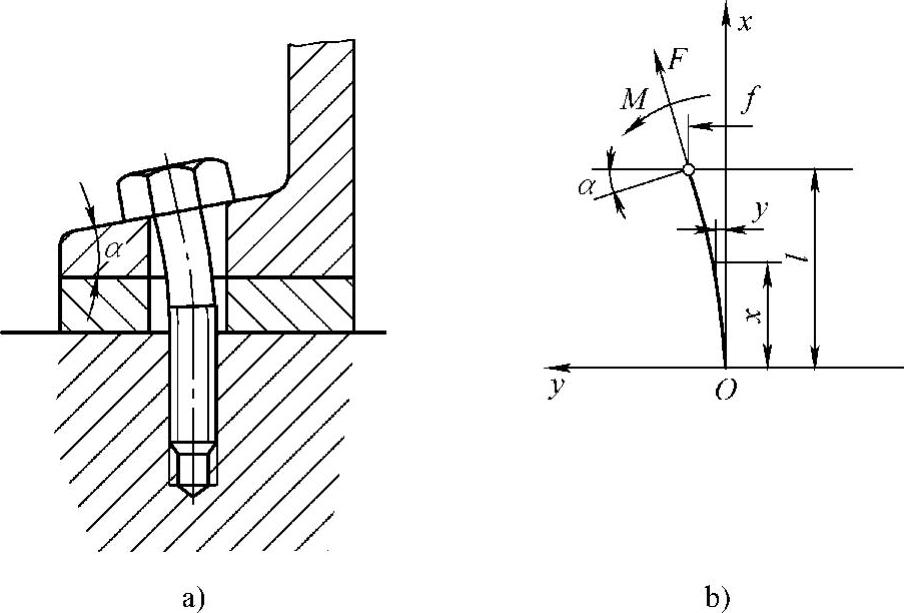
图4-19 拉弯联合应力计算

设螺母支承面与工件表面完全贴合。由预紧力和工作拉力产生的总轴向力为Q，其作用方向沿螺钉轴线方向。螺钉的弯矩方程式为（不考虑切应力的影响）：

EIy″=M+F[（l-x）sinα-（f-y）cosα]

式中f和α为x=l时螺栓的挠度和转角

令Fcosα/（EI）=λ²则λ=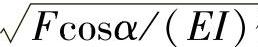代入上式可得

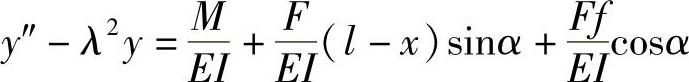
解上式可得

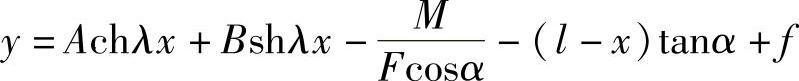
并可求得

y′=Aλshλx+Bλchλx+tanα(www.xing528.com)

以上两式中的常数A、B可由边界条件x=0时y=0，x=0时y′=0求得：

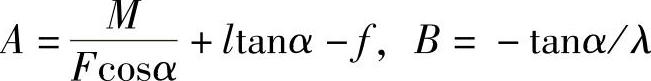
将求得的A、B代入y的方程式可得

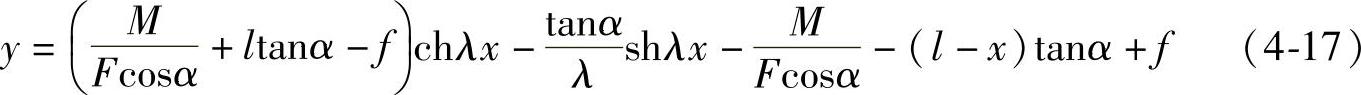
将边界条件x=l时y=f代入上式可求得最大挠度f；将式（4-17）两边对x求导，并代入边界条件x=l时，y′=tanα可得α：

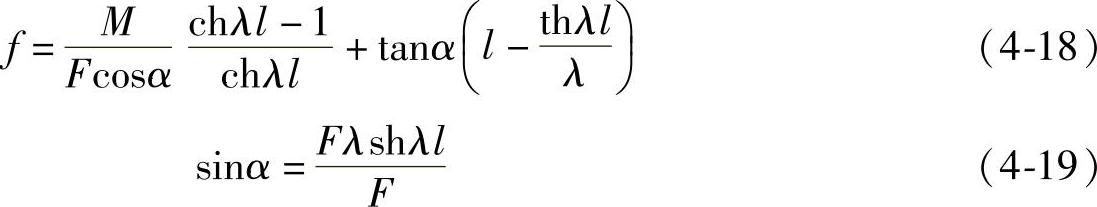
由以上所得各式可求根部弯矩M₀，由图4-19可得

M₀=M+F（lsinα-fcosα）

将式（4-18）代入上式得

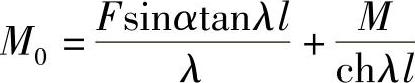
将式（4-19）代入上式可得

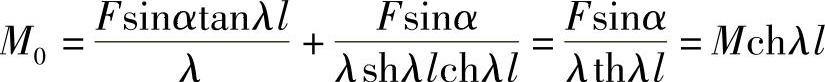
当α很小时，sinα≈α，cosα≈1，由预紧力F产生的螺杆的拉应力σ=4F/（πd²），则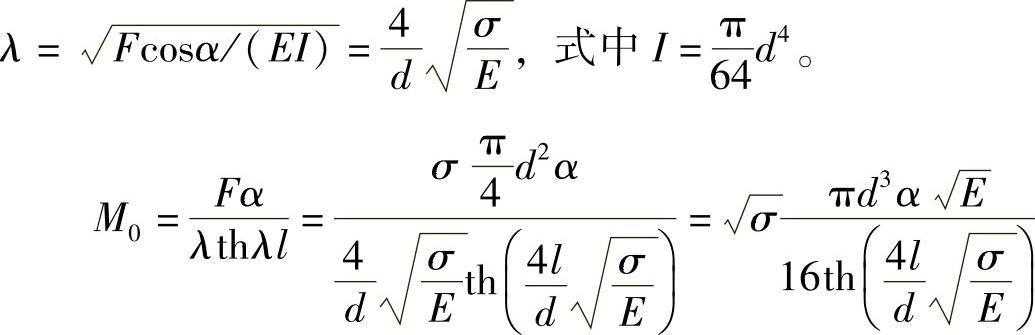

根部x=0处的弯曲应力σ_w为

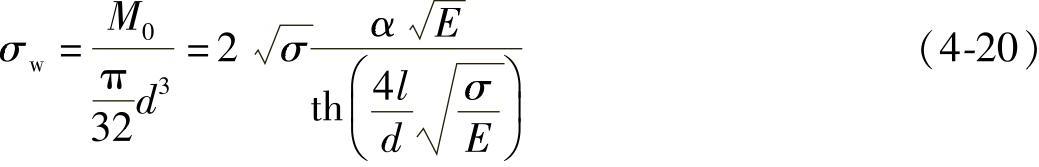
当预紧力很小时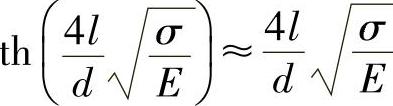，则式（4-20）可化为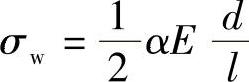即式（4-15）。

在图4-20中给出预加应力σ及螺栓长径比l/d对弯曲应力的影响，由式（4-20）计算而得，计算时，取α=0.5°，E=2.1×10⁵MPa。由图可以看出，l/d小，即螺栓短时，钉头偏转引起的弯曲应力大，预紧力大时弯曲应力的影响也比较显著，当l/d大于10～12时，继续加大l/d，σ_w降低不多。

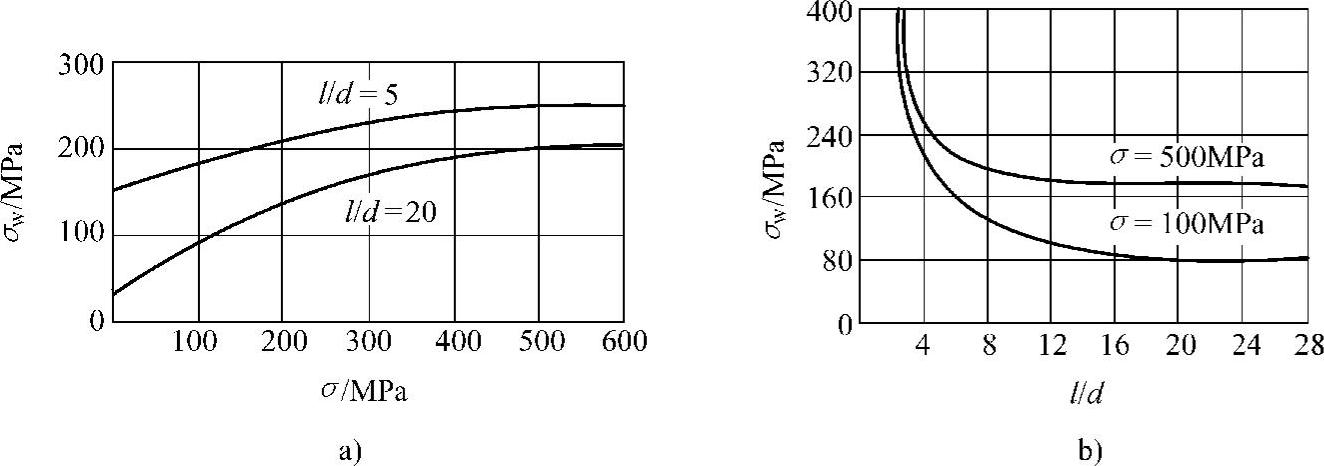
图4-20 预紧力σ和l/d对弯曲应力σ_w的影响

考虑双头螺柱或螺钉的螺纹部分拧入零件本体时，螺杆与螺孔的平均直径处的螺纹间隙Δ对弯曲应力的影响，螺纹部分所受弯曲应力为

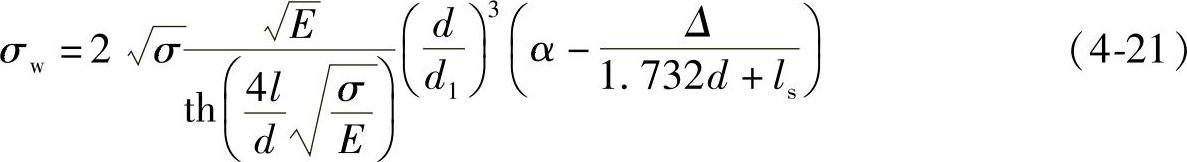
式中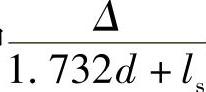考虑由螺纹之间的间隙使钉杆在螺纹孔中可以有少许转动从而减轻了钉头偏转角度的不利影响；其中Δ为螺钉与螺母螺纹平均直径之间的间隙，见式（4-22）。式中d为螺纹外径，l_s为螺纹配合部分长度。

式中Δ₁、Δ₂分别为螺钉及螺母的螺纹平均直径的公差；Δ_min为其最小间隙（图4-21）；K为螺钉重要性系数，对于重要螺钉取K=0.7～0.8，对于普通螺钉取K=1。

图4-22给出考虑间隙以后，钉头偏斜在钉杆中引起弯曲应力σ_w的情况；螺钉M10，l_s=15mm，α=0.5°，预加拉应力σ=200MPa。

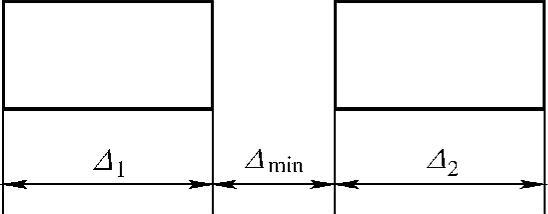
图4-21 螺钉螺母的平均直径 间隙Δ_min与公差Δ₁、Δ₂

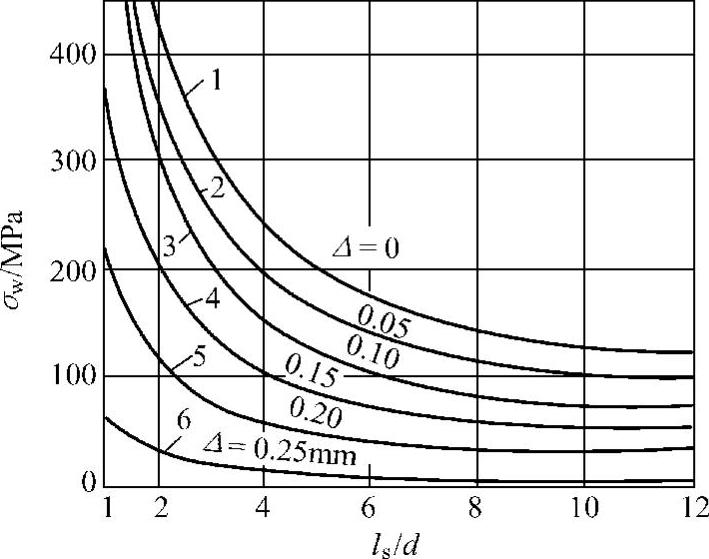
图4-22 考虑间隙影响后，钉头偏斜在钉杆中引起的弯曲应力