轴向外载荷下紧螺栓强度计算

图4-4a为一受轴向外载荷的紧螺栓，预紧力为F′，工作载荷为F，残余预紧力为F″，工作时螺栓所受的力为F₀、C₁、C₀为被连接件和螺栓的刚度。计算式为

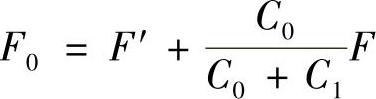
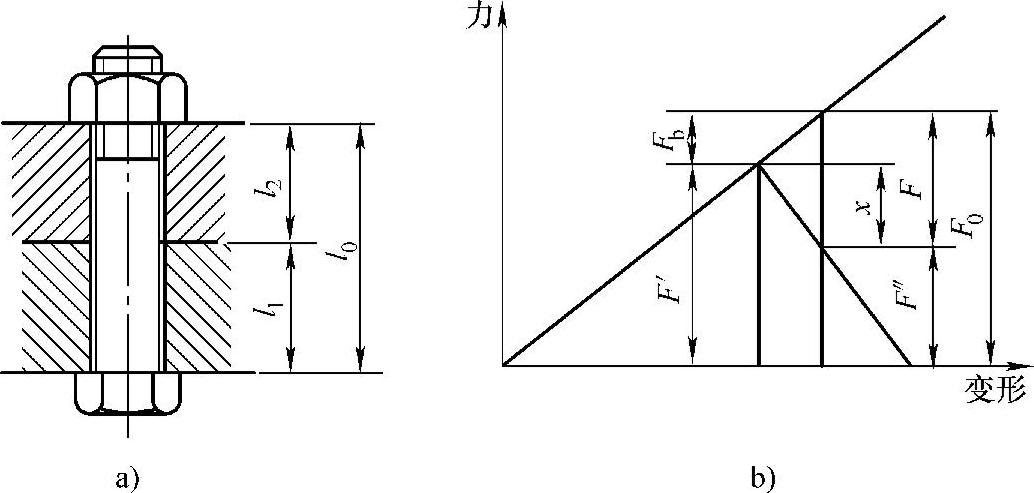
图4-4 受轴向外载荷的紧螺栓连接

1.螺栓刚度C₀的计算

由材料力学的应力应变关系，可知螺钉柔度λ₀为

式中 l₀——由螺母端面到螺钉头端面之间的距离。

对于l₀<6d的短螺栓应该考虑螺杆在螺母中的变形（或双头螺栓在机座中的变形）。简化计算公式为

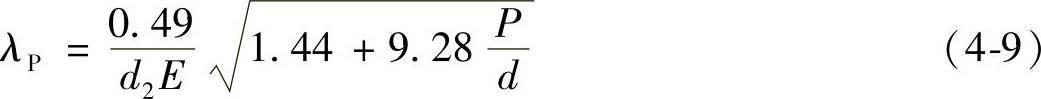
式中 P——螺距。

还可以用更简单的公式进行近似计算

当 d/P=6～10时 λ_P=（0.95～0.80）/（dE）

d/P=10～20时 λ_P=（0.80～0.70）/（dE）

如果螺母（或机座）与螺钉的弹性模量不同，分别为E_b和E_k，则可以采用

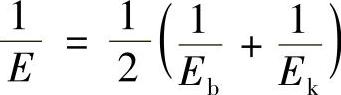
研究表明，螺纹连接的柔度λ_P与制造精度有关系，特别是螺纹牙形角影响很大。2～3级精度的螺纹比精确制造的螺纹柔度大2倍。预紧力大时，因为有塑性变形，制造误差的影响减轻了。当螺纹工作表面压强较小时（p≤10MPa），接触变形对柔度有很大的影响。当工作表面压强较大时，螺纹表面按标准（粗糙度Ra=3.2～12.5μm），接触柔度超过螺纹的柔度。在第一次工作时超过2～4倍，重复加载时超过0.5～0.8倍。而当表面粗糙度的参数值较小时（Ra≤0.10），对接触柔度影响不大。

钉头的柔度可以只按螺栓头部剪切变形柔度计算，钉头柔度λ_b=0.15/（hE_b），式中h为钉头高度。

综上所述，对于图4-5所示的短螺栓连接的柔度为

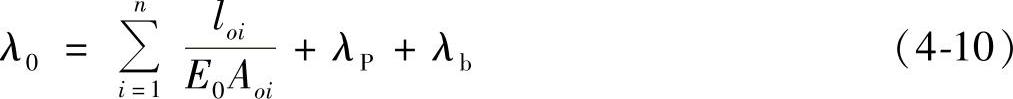
式中 l_oi——螺栓各部分长度；

A_oi——螺栓各部分断面面积。

2.被连接件刚度计算

图4-6中给出一些计算被连接件刚度影响区时采用的各种假设和计算结果的比较。

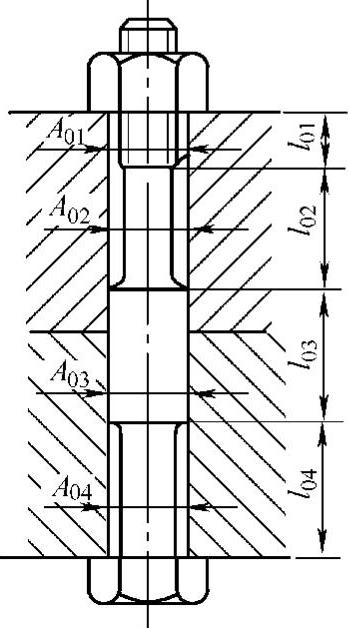
图4-5 螺栓柔度

计算被连接件刚度的方法很多，过去多采用45°圆锥平均影响区假设（图4-6d），而目前多采用锥顶角2α影响区假设。图4-7中给出螺钉头压紧被连接件的影响区为半锥顶角为α的空心截圆锥，内部有一直径为d₀的圆柱形孔。

图4-7a中被连接件很薄（l₁<d₀）时可以用圆柱代替圆锥影响区，被连接件的刚度为C₁，柔度为λ₁，则

式中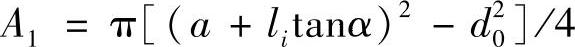

当l₁≥d₀时应按空心截圆锥计算（图4-7a）。

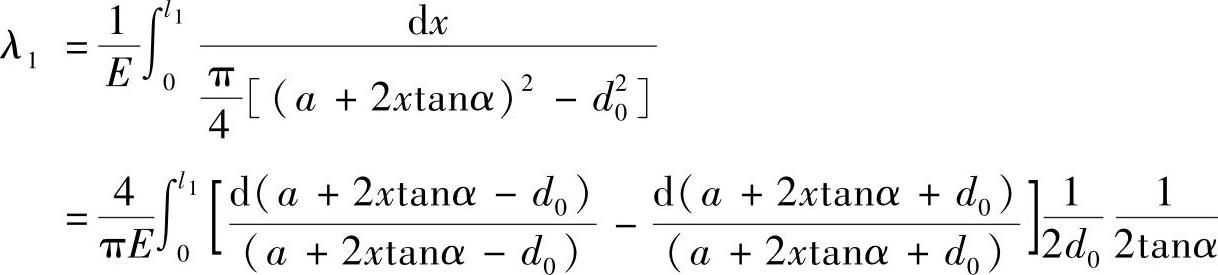
得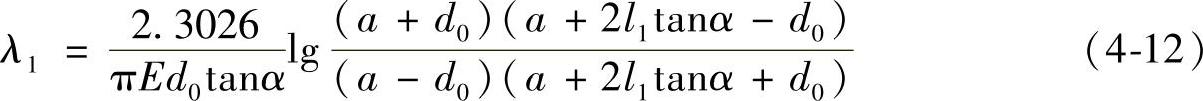

对图4-7b则在上式中以l代替2l₁，以4.6052代替2.3026得

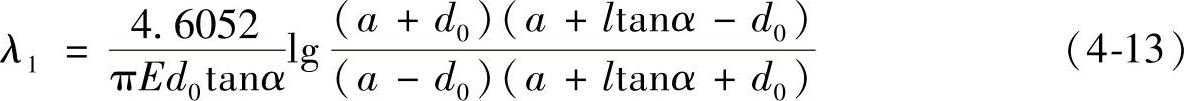
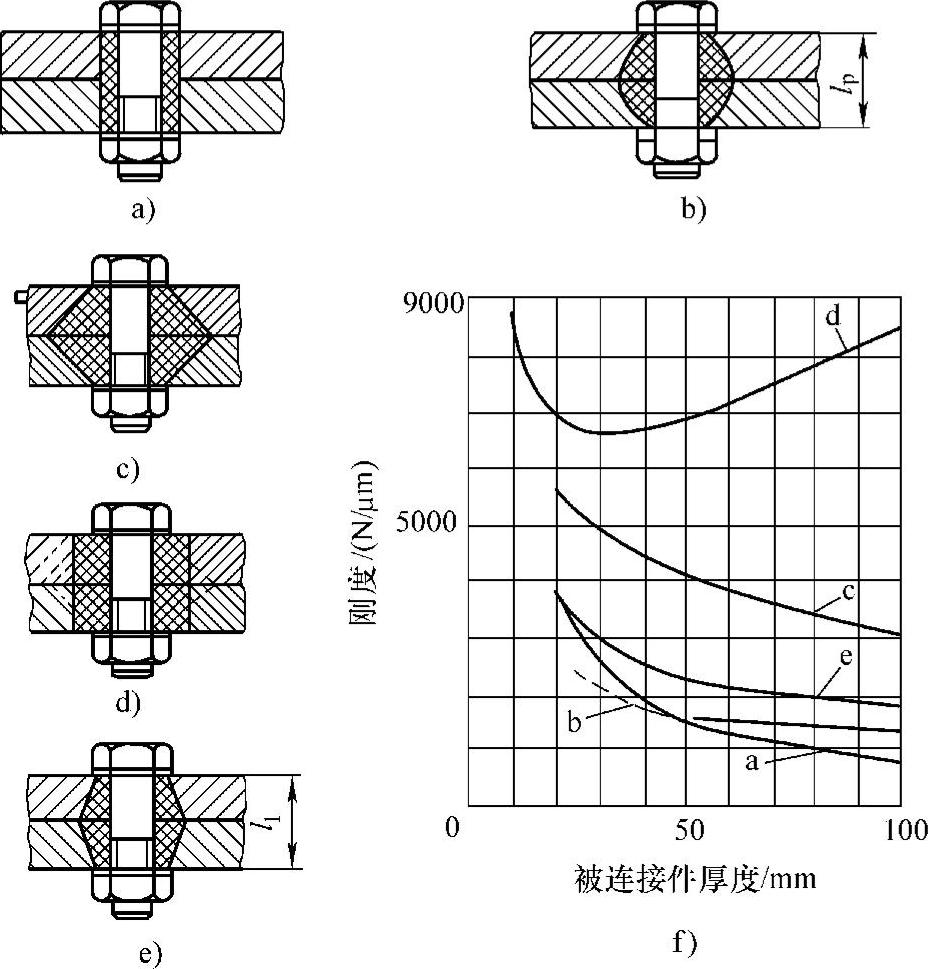
图4-6 计算被连接件刚度时采用的影响区(www.xing528.com)

a）圆柱影响区假设 b）曲线影响区假设 c）45°圆锥影响区假设 d）45°圆锥平均影响区假设 e）锥顶角2α影响区假设 f）按以上五种假设求得的被连接件刚度C₁

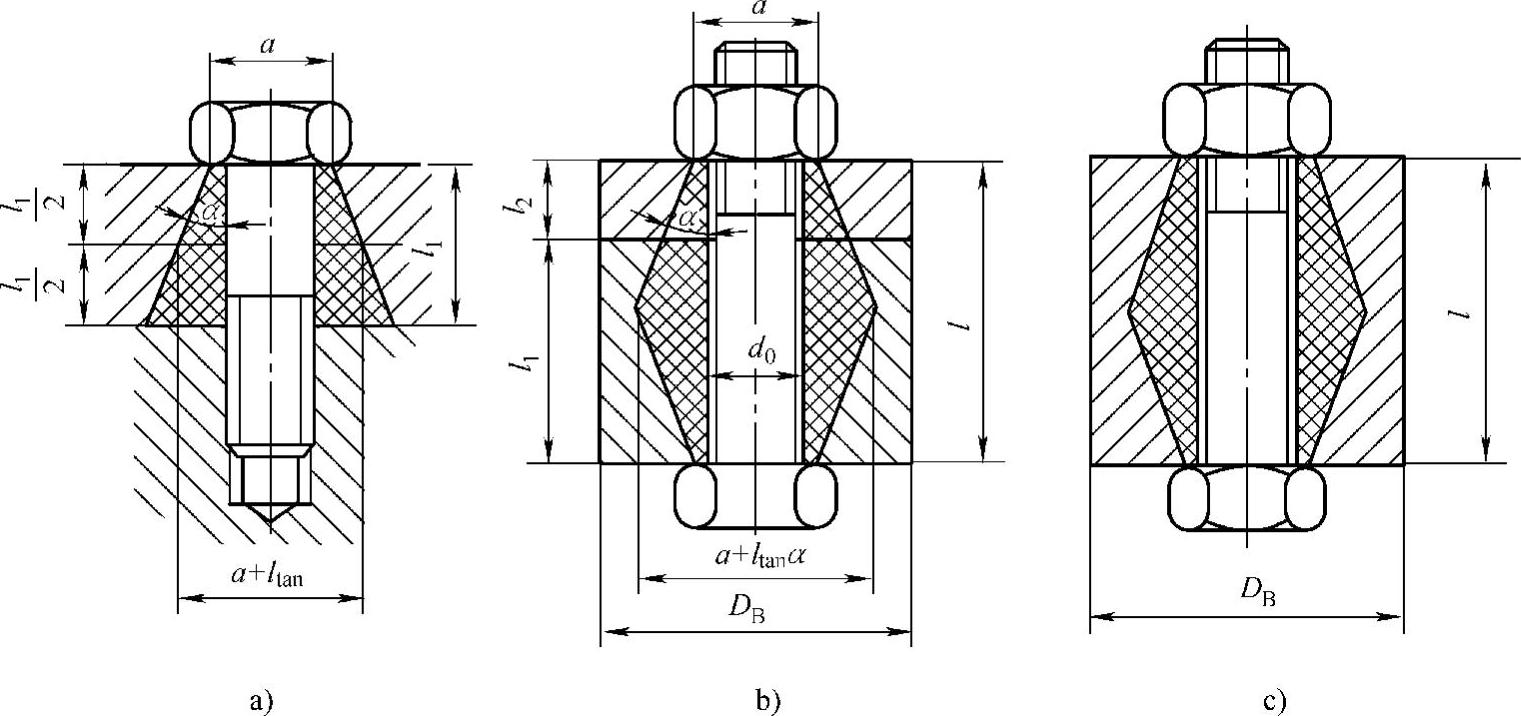
图4-7 被连接件的影响锥

a）螺钉连接 b）螺栓连接，组合被连接件 c）螺栓连接，整体被连接件

在计算中取tanα=0.4～0.5，即α=22～27°。上述公式比较复杂，下面介绍

几种简化计算公式：

В.К.Данилов给出的简化公式，用于l<8d

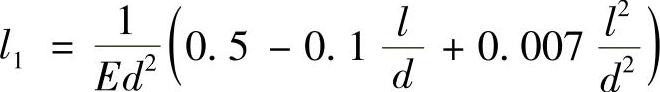
Weiβ、Wallner建议采用等效圆筒，其断面面积：

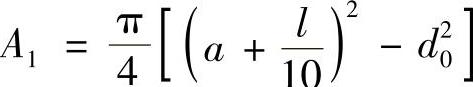
Junker建议采用等效圆筒断面积为：

钢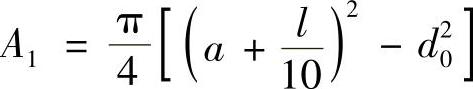

铸铁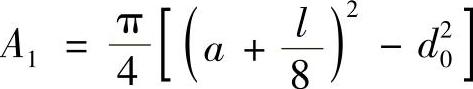

铝合金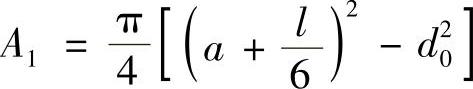

在一般机械零件（机械设计）教材中，常采用相对柔度x进行计算。x=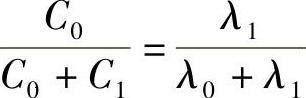，当被连接件为金属件时（不用垫片）x=0.2～0.3。图4-8给出相对柔度的试验值。D_B为试验所用被连接件的外径。

3.受轴向力紧螺栓计算

图4-9a表示受轴向力紧螺栓连接中，作用力的不同位置。外载荷F作用在被连接件中间，则被连接件由i+1至j-1受拉力（预紧力减小），螺栓也受拉力，而被连接件1～i，j～n受压力。其受力情况如图4-9b、c。在图中，把零件分为两组，螺栓零件组（图4-9b）和被连接件组（图4-9c）。

设在受有预紧力F′的螺栓连接的接合面处，作用外载荷F以后，接合面处被连接件之间的压力变化为X，则其大小可以由螺钉系统的变形Δl_b与被连接件系统变形Δl_k相等的条件（即接合面不分离的条件）求得（图4-4）。

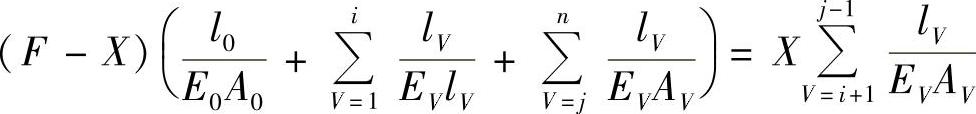
在公式中引入柔度符号，并经整理得到

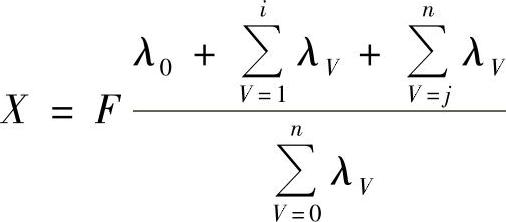
在图4-4中由于外载荷F的作用引起的螺栓载荷增加量F_b为

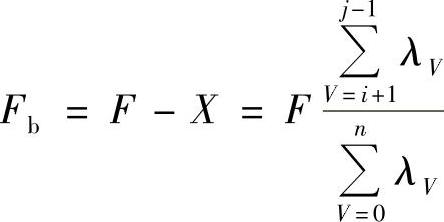
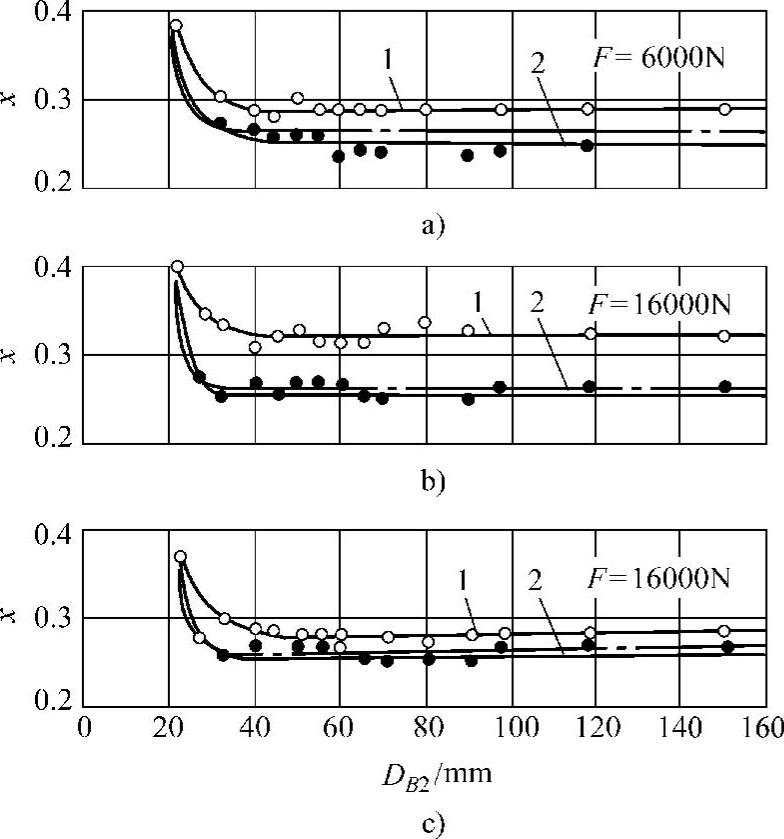
图4-8 相对柔度与试件直径D_B及 预紧力F′和外载荷F的关系

图a、b中，曲线1—F′=16000N，曲线2—F′=32000N，整体被连接件（无接合面）l=36mm，图c中，F′=32000N，1—组合被连接件，l₁=l₂=18mm；2—整体被连接件l=36mm，点画线—理论计算结果，实线—实验结果。

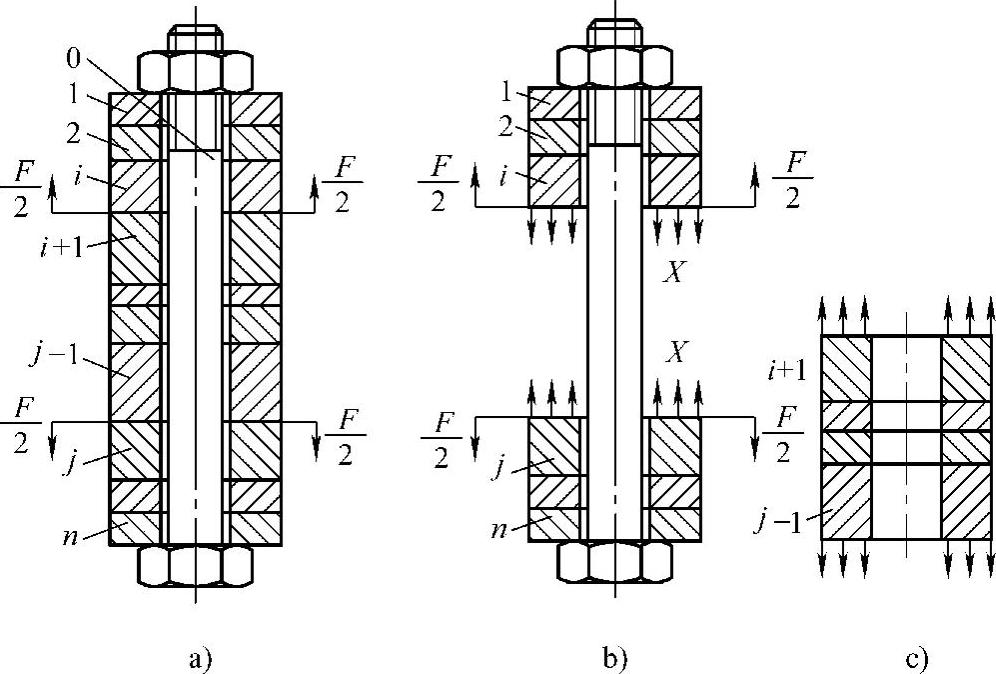
图4-9 受轴向外载荷紧螺栓力作用点的影响

相对柔度x=F_b/F，由此可知

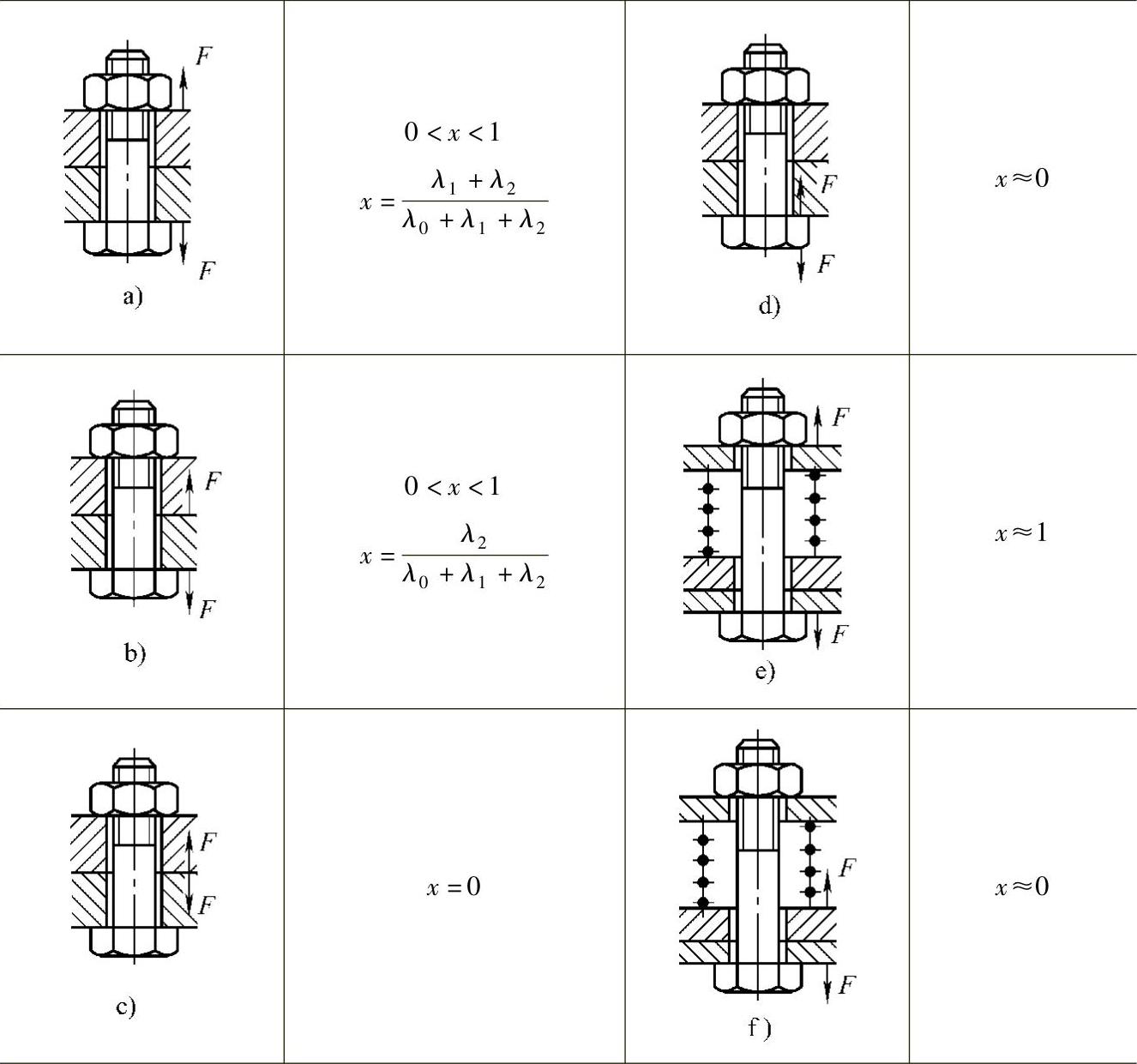
图4-10 各种外载荷情况的x值

图4-10给出各种典型情况的相对柔度x值。图4-11为两种不同的结构，图4-11a的结构可认为近似于图4-10中的图b，图4-11b的结构可认为接近于图4-10中

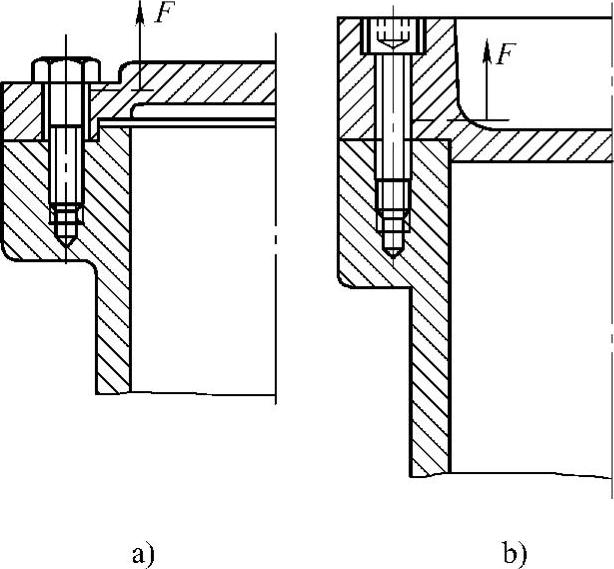
图4-11 按结构确定外载荷作用点

的图c。因此在图4-11中，图a的结构由螺钉连接的疲劳强度来分析比图b的结构差。