螺纹连接力分布优化方案

螺纹连接是通过螺纹的工作表面传力的（图4-1）。各螺纹牙之间载荷不是均匀分布的，而一般《机械设计》中都按均匀分布计算而取较低的许用应力。为精确计算各扣螺纹受力，必须求解静不定的力分布问题。图4-2给出螺纹连接各扣螺纹的力传递路线，由图可以看出螺纹中各扣螺纹间的力分布与螺母的支承结构有关。图4-3是可以适用于图4-2中两种螺母结构的通用模型。对于图4-2中的两种结构，F_z、F_d取不同值即可。对受压螺母F_d=F，F_z=0；对受拉螺母F_z=F，F_d=0。

由图4-3第i扣螺纹的受力情况，根据节点A力的平衡关系可得

F_B（i-1）-^FBi^-FGi=0 （4-1）由节点B处力的平衡关系可得

F_Mi^-FM（i-1）-^FGi=0 （4-2）此外，根据螺纹变形与螺杆、螺母变形协调条件可得以下关系。

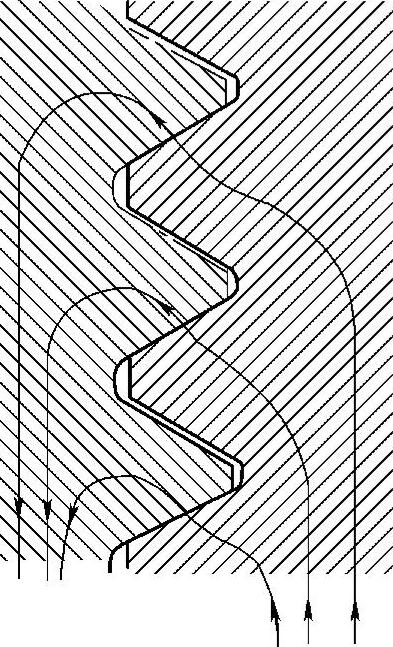
图4-1 螺纹传力情况

图4-2 螺母支承结构

a）受压螺母 b）受拉螺母

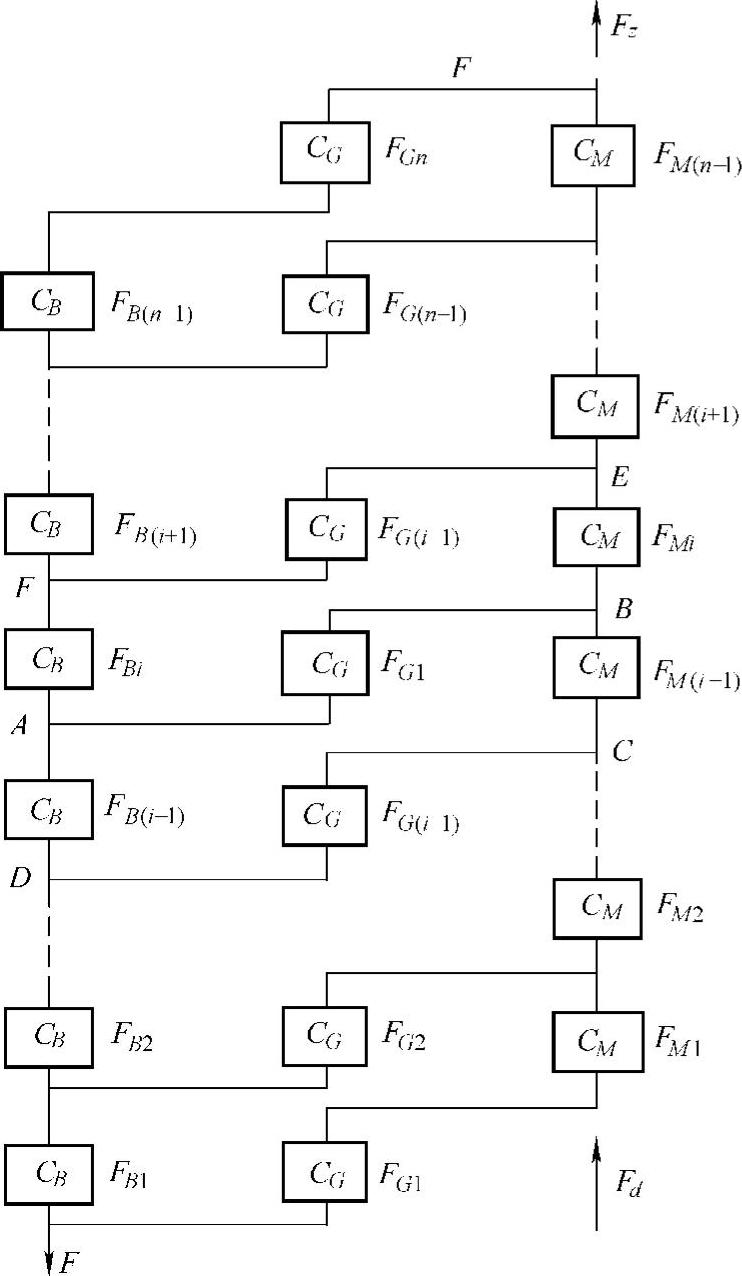
图4-3 螺纹副受力分析通用模型

C_B—螺钉杆钢度C_M—螺母刚度C_G—螺纹结合部分的刚度

由间格ABCD的变形协调条件

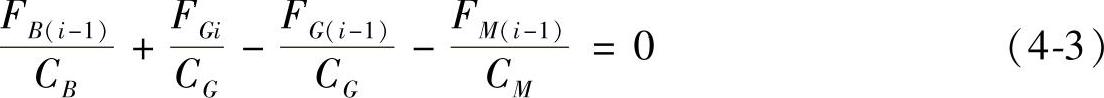
由间格ABEF的变形协调条件

以上两式相减得

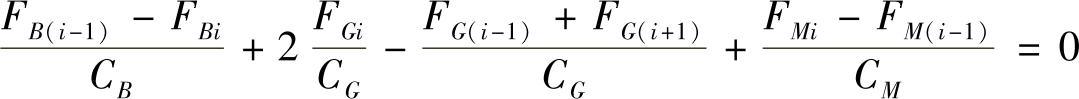(www.xing528.com)

将（4-1）（4-2）式代入上式并整理之，得：

上式对i=2～（n-1）都是可用的，对于i=1和i=n时，由不同的支承条件采用下列公式：

对于受压螺母（F_d=F，F_z=0）

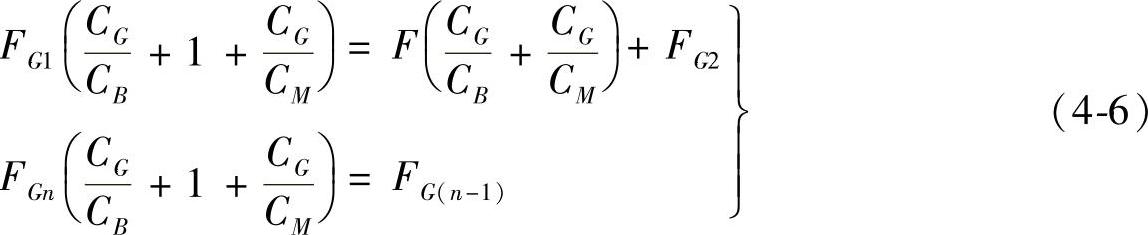
对于受拉螺母（F_z=F，F_d=0）

式中，C_G、C_B、CM可以由以下公式求得

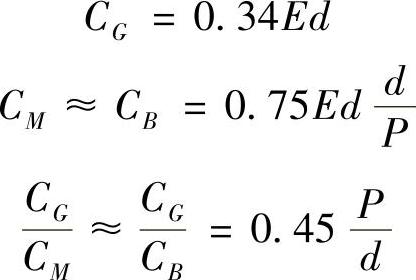
式中 d——螺纹外径；

P——螺距；

E——螺钉及螺母的弹性模量。

在利用以上公式计算时，可以近似地取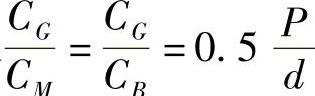。可以由此求得图4-2中两种结构的力分布情况。

西田正孝用计算和三维冻结光弹性试验方法，得到直径为1英寸的惠氏螺纹，在螺母受压时，螺纹牙数分别为6、8、10的力分布，见表4-1。

表4-1 螺纹牙受力分布 （%）