多重化整流电路的优化设计

为减少输入谐波电流，将几个桥式整流电路按某种方式联结，构成多重化整流电路，采用自换相整流电路可以提高位移功率因数。多重化输入变压器的设计方法很多，下面介绍其中一种多重化的原理。

为简化分析，在下面分析中不考虑变压器漏抗引起的重叠角，并且假设整流变压器各绕组的线电压之比为1∶1。假定直流环节电流为恒定值，这种条件一般在电流源型变频器中近似成立，在电压源型变频器中，直流环节电流则为脉动状，通过设置适当的LC滤波器，直流电路脉动可以很小。

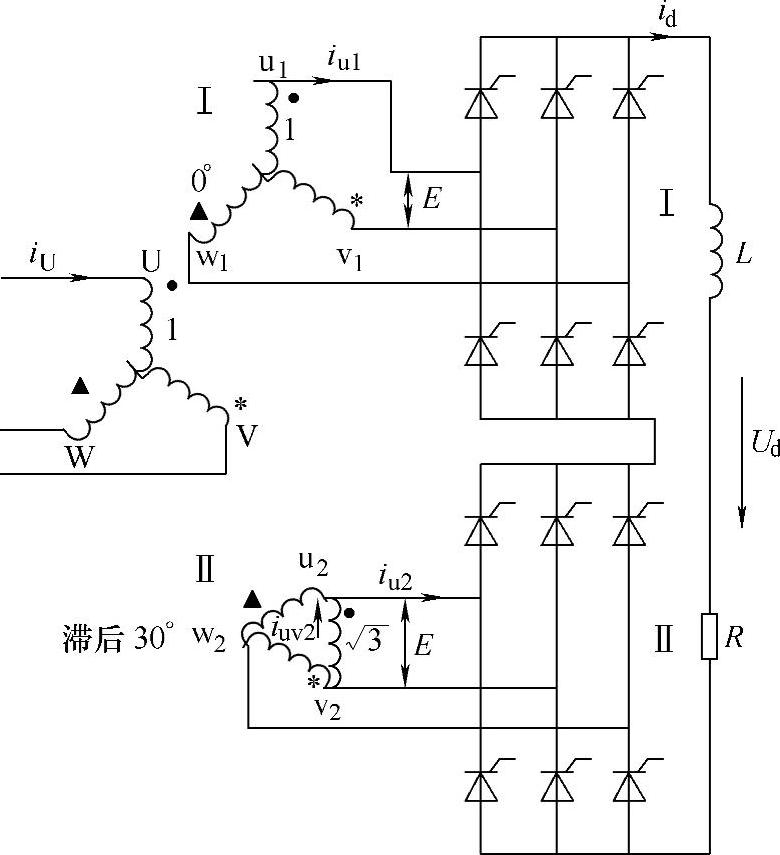
图6-29 12脉波整流电路结构

1.移相30°构成的12脉波整流电路 图6-29是这种电路的原理图，整流变压器二次绕组分别采用星形和三角形联结，构成相位差30°、大小相等的两组电压，加到两组整流桥上。因绕组联结不同，变压器一次绕组和两组二次绕组的匝比如图所示，为1∶1∶3。

图6-30为该电路输入电流波形图。其中，图6-30c的i′_uv2是第II组整流桥i_uv2折算到变压器一次侧U相绕组中的电流。图6-30d中输入电流i_U为图6-30a的i_u1和图6-30c的i′_uv2之和。

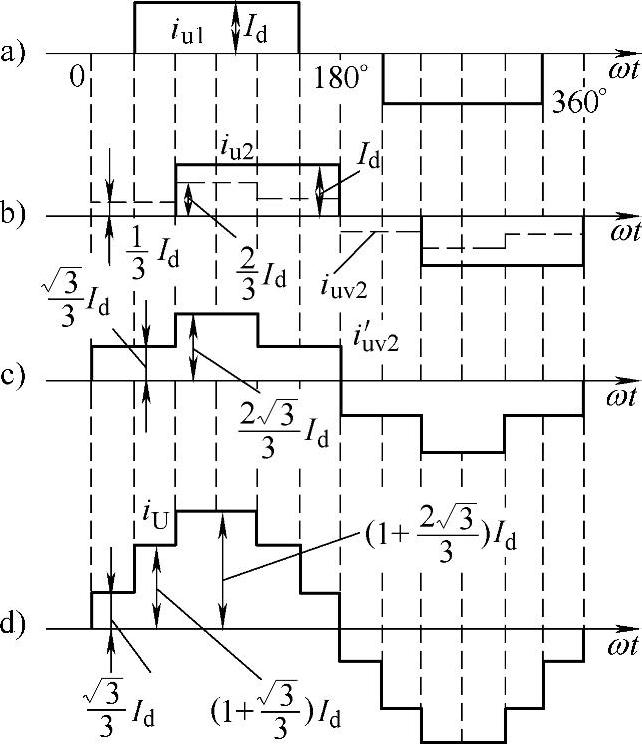
图6-30 12脉波整流电路电流波形

对图6-30波形i_U进行傅里叶分析，可得其基波幅值A₁和n次谐波幅值A_n，分别如下：

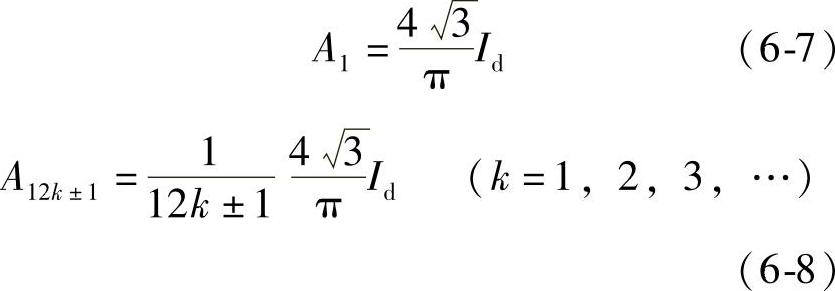
即输入电流谐波次数为11、13、23、25、35、37…。其幅值与次数成反比而降低。

该电路的其他特性如下：

输入电流有效值I₁=1.577I_d

输入电流总畸变率THD_i=0.1522

位移因数cosφ₁=cosα基波因数v=（A₁/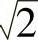）/I₁=0.9886功率因数λ=vcosφ₁=0.9886cosα

2.移相20°构成的18脉波整流电路 图6-31是其电路图，其中整流桥采用简化画法。对于整流变压器来说，采用星形、三角形联结组合无法移相20°，这里第Ⅰ、Ⅲ绕组采用了延边三角形曲折联结。这种联结的每相由对应于一次侧不同相的绕组串联而成，改变所取绕组的匝比可以实现任意角度的相移。以一次侧每相绕组为1时，通过求解图6-31中第I组桥u₁相绕组的三角形可得图中绕组N_x、N_y的匝数分别为

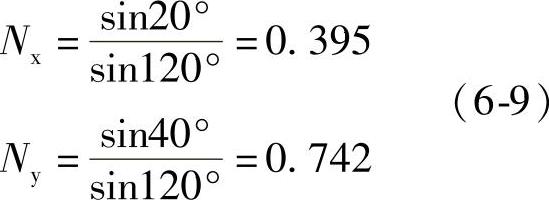(www.xing528.com)

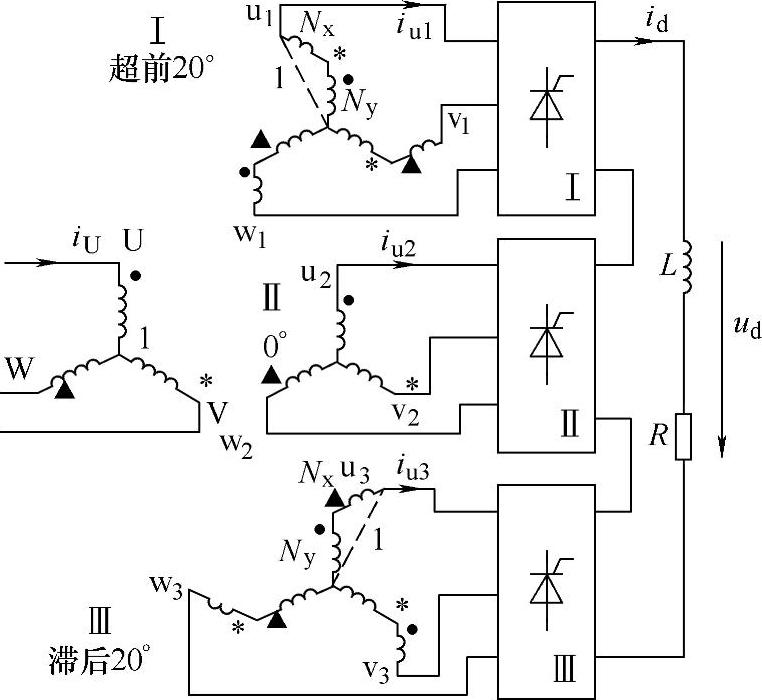
图6-31 18脉波整流电路结构

图6-32为整流变压器一次侧输入电流i_U波形，其基波和谐波幅值分别为

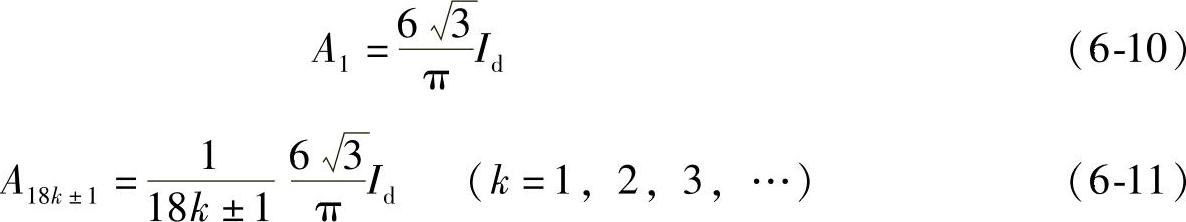
即输入电流谐波次数为17、19、35、37、53、55、…。其幅值与次数成反比而降低。

该电路的其他特性如下：

输入电流有效值I₁=2.351I_d

输入电流总畸变率THD_i=0.1011

位移因数cosφ₁=cosα基波因数v=（A₁/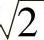）/I₁=0.9949

功率因数λ=vcosφ₁=0.9949cosα

从以上分析可以看出，采用多重联结方法可以大幅度减少输出电流的谐波含量，从而提高了功率因数。值得注意的是，整流电路的输出电压是各三相整流桥输出电压之和，但输入电流有效值小于各输入电流有效值之和。这是因为直流输出电压是平均值，而输入电流却是相位不同的电流分量相加后再求有效值。

通过两个相角差30°的变压器绕组分别供电的两个三相整流电路可构成12脉波整流电路，其网侧电流仅含12k±1次谐波；类似地，通过依次相差20°的三个变压器绕组分别供电给三个三相整流可构成18脉波整流电路，其网侧电流仅含18k±1次谐波；通过依次相差15°的四个变压器绕组分别供电给四个三相整流桥就可获得24脉波整流电路，其网侧电流仅含24k±1次谐波；通过依次相差12°的五个变压器绕组分别供电给五个三相整流桥就可获得30脉波整流电路，其网侧电流仅含30k±1次谐波。

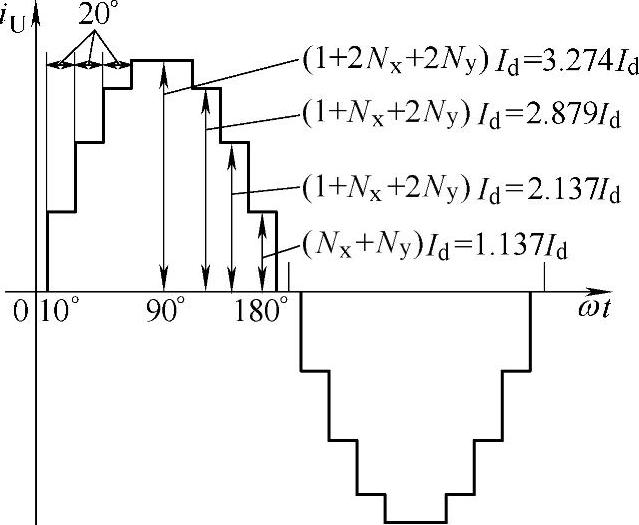
图6-32 18脉波整流电路输入电流波形

综上所述，以m个相位依次相差π/3m的变压器绕组分别供电给m个三相整流桥就可获得6m脉波整流电路，其网侧电流仅含6mk±1次谐波，而且各次谐波电流的有效值与其谐波次数成反比，而与基波电流有效值的比值是谐波次数的倒数。另外，其位移功率因数均为cosα，不随整流脉波数的增加而提高，但基波因数随着整流脉波数的提高而提高。所以总体输入功率因数也跟着提高。对于二极管不可控整流电路而言，相电流相对于相电压的延迟角度α一般小于15°，对应的位移功率因数大于0.966，所以采用多重化（18脉波以上）的二极管整流电路，总的输入功率因数基本上可保持在0.95以上。