电压空间矢量优化分析

下面要说明的是，在逆变器的开关模式作用下形成的异步机的电压空间矢量。

异步电动机三相绕组在空间对称安放，三个绕组的轴线在空间依次互差120°电角度。最经典的情况是，通入三相对称电流会产生圆旋转磁场。旋转磁链可以用空间旋转矢量表达。相应的定子电流，外施电压也可以用空间旋转矢量表达。空间矢量有很多具体内容，在这里不准备展开。直接写出表达式，设定子全磁链空间矢量表达成

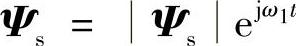
不计定子电阻压降时，则外加电压

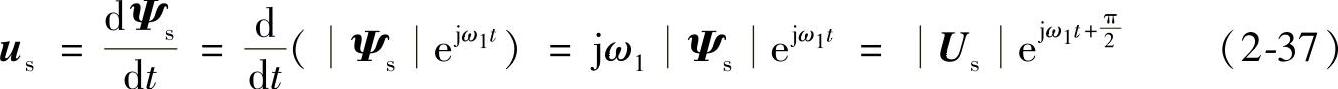
式中 U_s=ω₁Ψ_s=2πf₁Ψ_s为电压空间矢量的模。

由式（2-37）可见电压空间矢量在空间引前于磁链矢量90°。

如图2-60所示的三相电压型逆变器可能的开关状态，只有2³=8种状态。按180°导电型控制六个元件组合起来的开关状态为（6、1、2），（1、2、3），（2、3、4），（3、4、5），（4、5、6），（5、6、1），还有两种状态（4、6、2）和（1、3、5）。这8种开关状态，对应着8个电压空间矢量，用u₁、u₂、u₃、u₄、u₅、u₆和u₀、u₇作为代号。我们通常还用二进制代码来表示它们。u₁：（100）代表6、1、2导通，u₂：（110）代表1、2、3导通，……。这意味着U、V、W三个端点的对应桥臂对，上臂导通为“1”状态，下桥臂导通为“0”状态。这些状态有8种，列在表2-5中。

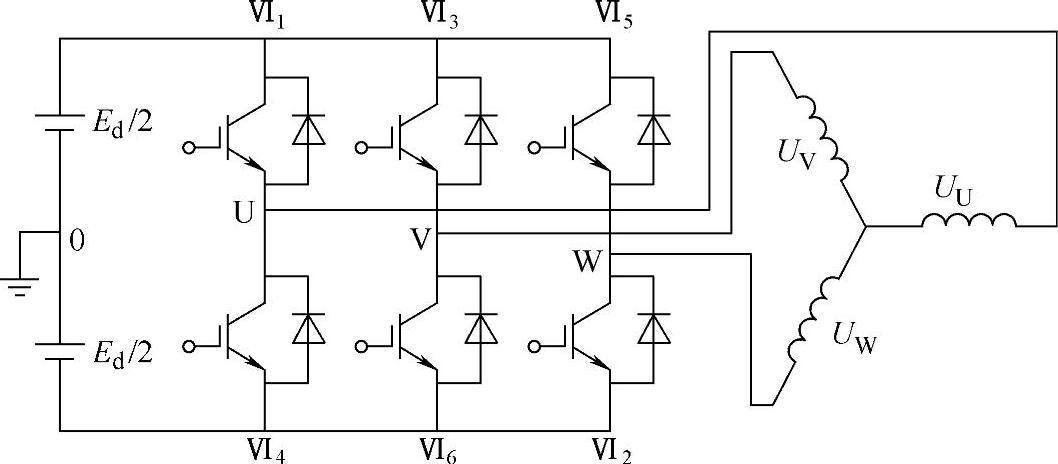
图2-60 变频器感应电动机系统

表2 - 5 逆变器的8种开关模式与合成电压空间矢量

下面我们画出八种开关状态所对应的电压空间矢量图。

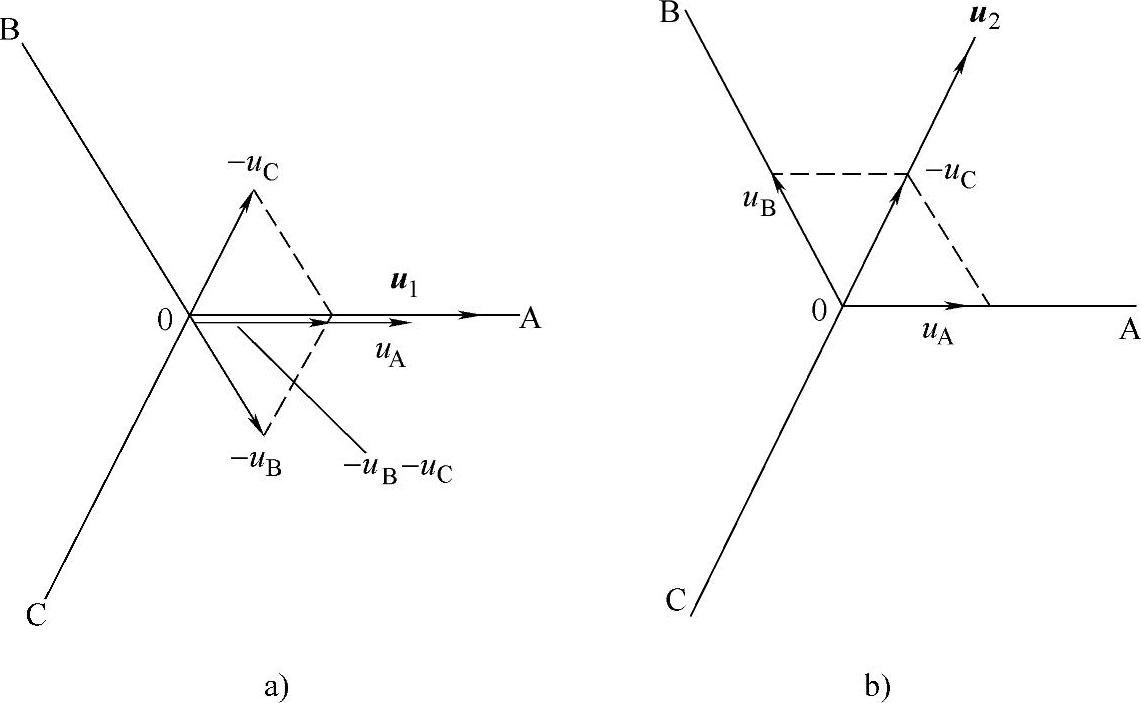
图2-61 电压空间矢量u_i的形成

a）100开关模式 b）110开关模式

用图2-61来说明，在定子的三相静止坐标系内作图。以100开关模式为例，用相电压矢量来合成空间矢量。U相为“1”，画在U轴的正方向上，模为E_d/2；V相为“0”，画在V轴的反方向上，模为E_d/2；W相为“0”，画在W轴反方向上。三个相电压矢量的合成矢量为电压空间矢量u₁，在U轴的正方向上，模为E_d。用相类似的方法，画出110开关模式下的电压空间矢量如图2-61b所示，u₂在V轴的反方向上，模为E_d。而000和111两种状态为零电压矢量，可以用图中O点（原点）表示。(www.xing528.com)

六个非零矢量和两个零矢量画在一起，如图2-62a所示。

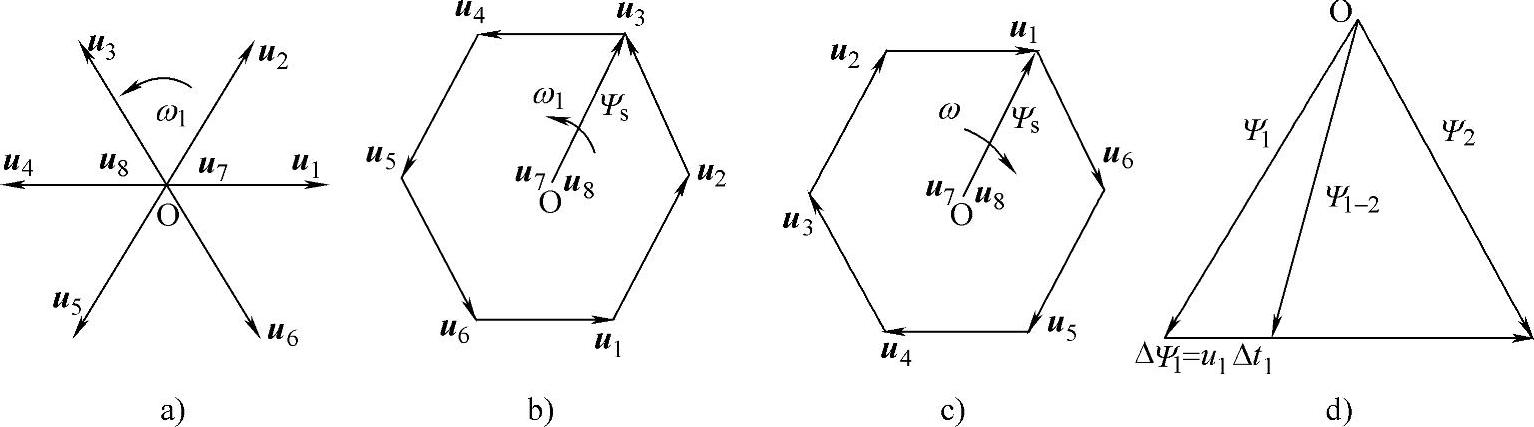
图2-62 电压空间矢量

a）电压空间矢量 b）Ψ_s轨迹（逆时针） c）Ψ_s轨迹（顺时针） d）Ψ_s的变化过程

在图2-62b中，我们把电压空间矢量画成了闭合正六边形。实际上定子磁链空间矢量Ψ_s的矢头轨迹就是这个正六边形。Ψ_s旋转矢量的箭头端沿着6个电压空间矢量的箭头方向以ω₁角速度旋转，即逆时针方向旋转。再看图2-62c，如果改变6个空间电压矢量的切换顺序，由原来的1→6变成6→1的切换顺序，Ψ_s将反转，即顺时针方向旋转。

式（2-37）的反运算，表达为

Ψ_s=∫du_sdt=u_kt_k+Ψ_s0=ΔΨ_k+Ψ_s0（k=0，…，7）（2-38）

上式说明，Ψ_s的轨迹是u_k的不断切换决定的。

由上式可见，Ψ_s的变化与u_k的作用时间有关，也与u_k的幅值有关。式（2_-38）的矢量图图形表达见图2-62d所示。由电压空间矢量u₆切换成u₁的初瞬算起，经过时间Δt₁磁链的变化为

ΔΨ_s=u₁Δt₁=ΔΨ₁

即经过Δt₁时间，Ψ_s由原来的Ψ₁变成Ψ_1-2。当ω₁t₁=π/3，Ψ_s由原来的Ψ₁变成Ψ₂。这表示在ω₁t₁=π/3对应的时间内，由于u₁的作用Ψ_s沿u₁的方向前进了π/3电角度。

另外，在这个π/3区间内，严格地看Ψ_s并不绝对地落后于u₁以90°，而平均地看才是落后90°的。

图2-63示出了六脉波三相逆变器的磁场轨迹和相电压波形图。图2-63a中Ψ_s∗是磁链幅值的希望值，六边形磁场轨迹，使得Ψ_s是波动的。波形范围为ΔΨ_s。为了比较在图2-63b和图2-63c中分别画出了未插入零矢量和插入零矢量的两种情况下的相电压波形。可见插入零矢量之后，由于Ψ_s出现停顿，Ψ_s转速减慢，使得波形周期变大即频率变低，零矢量使电机端短路，也必然使电压值减小。如图，周期增到5/3倍，频率和电压降到了原来的3/5。保证了U/f=常数的控制。

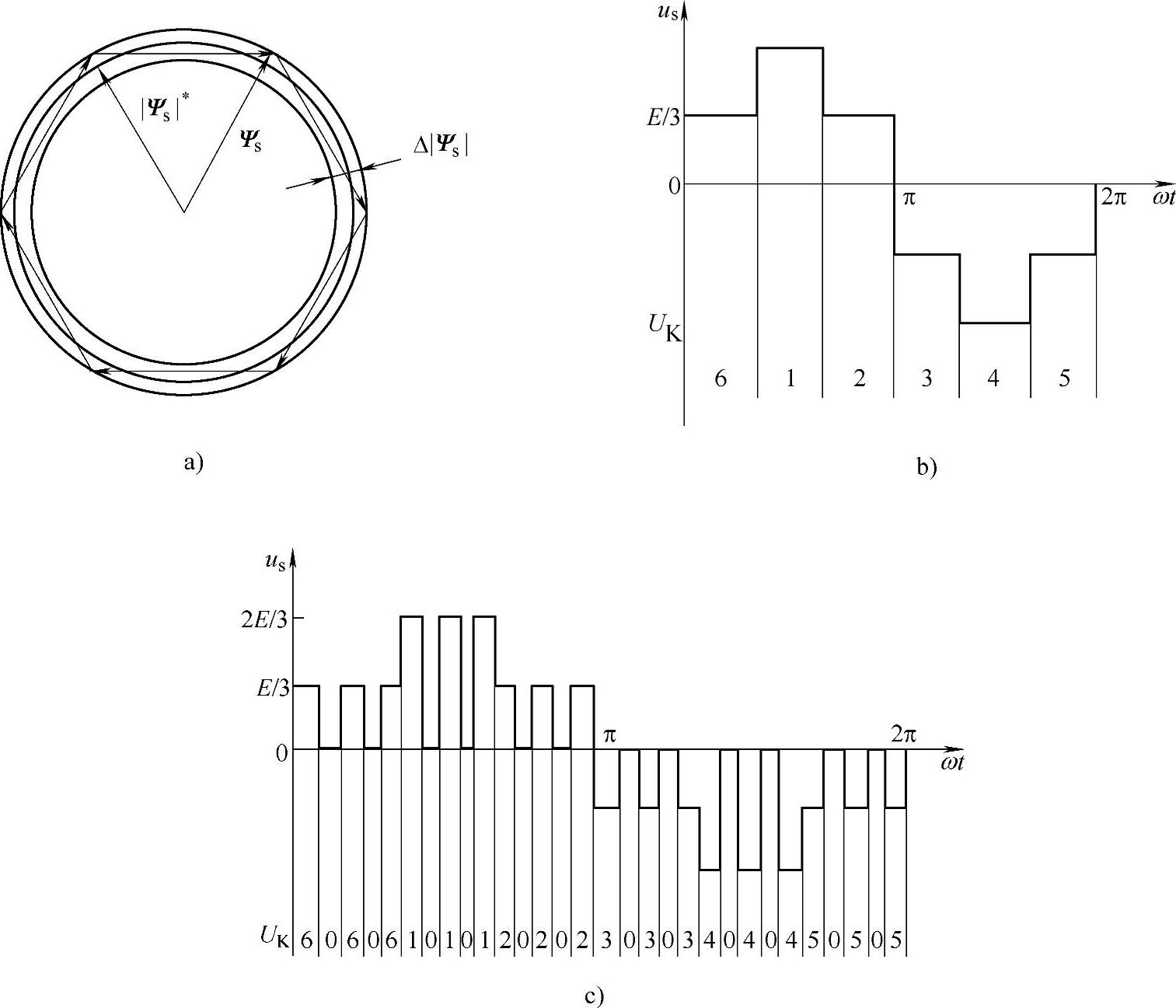
图2-63 六脉冲电压空间矢量与波形

由式（3-38）可见，Ψ_s的旋转角速度与u_K的幅值有关，也就是与E_d有关，调节E_d的大小自然可以调速，但大多数变频器的E_d是不可调的，因为E_d的调整需功率电路起作用是要增加成本的。所以用插入零矢量的办法调节转速是一个有效的办法。不必担心，如图2-22所示，使用最多的SPWM控制，插入零矢量的比例也是不小的。