气隙磁链参变量下的转矩特性优化分析

图2-43示出了不计铁损耗时异步电动机的T型等效电路。

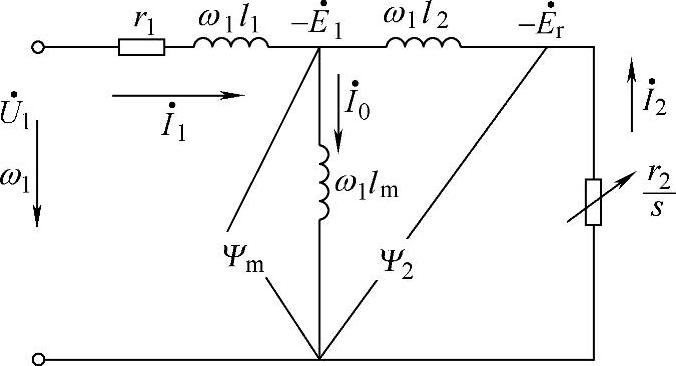
图2-43 异步电动机的T型等效电路

由等效电路可知

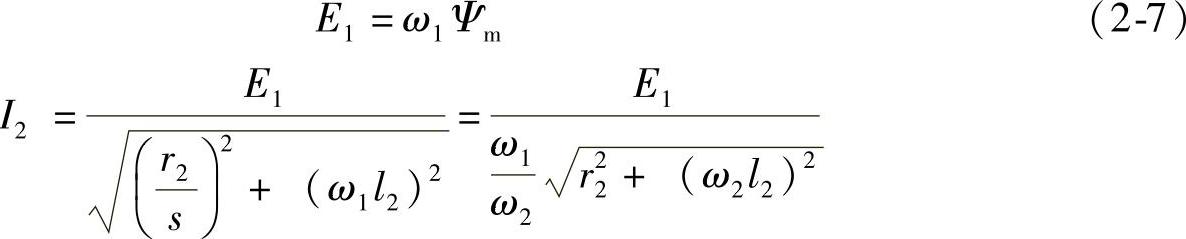
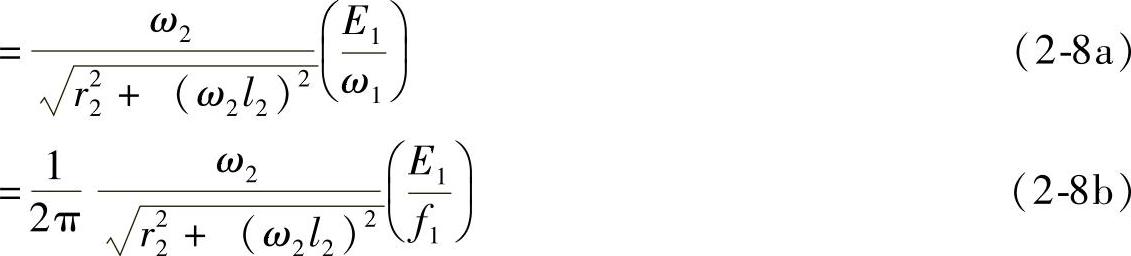
式中 E₁——定子相电动势；

ω₁——定子角频率；

I₂——转子相电流；

s——转差率，s=ω₂/ω₁；

ω₂——转差角频率；

r₂——转子相电阻的折算值；

l₂——转子相漏感的折算值。

由于异步电动机的电磁转矩等于电磁功率P_m除以同步角速度Ω₁

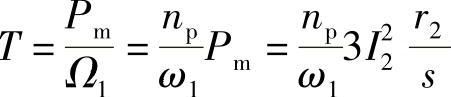
将I₂代入上式

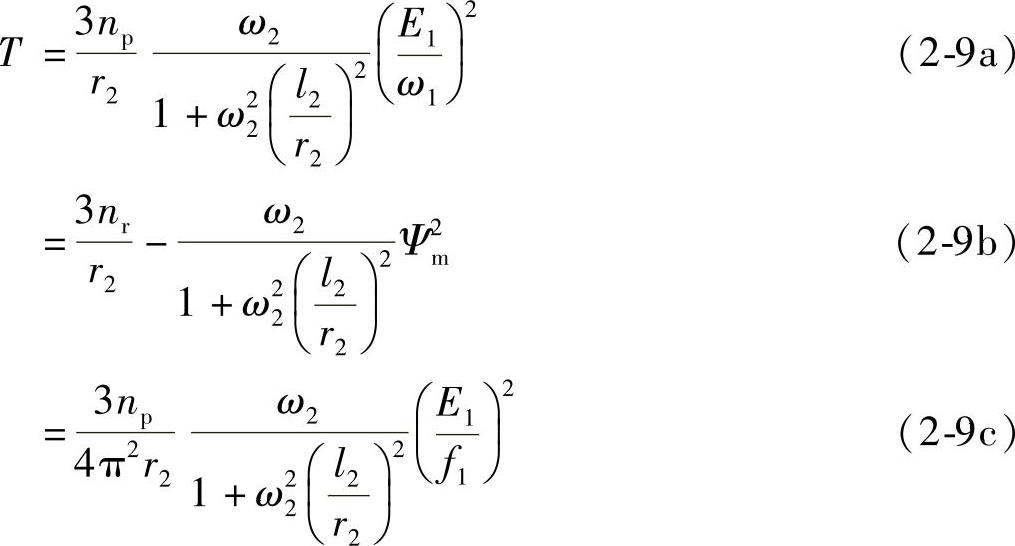
式中 n_p——极对数。

上述表达式是以转差角频率ω₂为自变量的转矩特性，T是关于ω₂的二次曲线。令dT/dω₂=0求出产生临界转矩时的临界转差角频率ω_2m：

ω_2m代回到式（2-9）中，得临界转矩为

画出T=f（ω₂）和I₂=f（ω₂）的关系曲线，如图2-44a所示。由图可见，在变频传动过载能力允许的范围（通常为1.5～2.0倍）内，T=f（ω₂）和I₂=f（ω₂）基本上是直线。稳定运行时，ω₂的大小代表着负载转矩T_L的大小。(www.xing528.com)

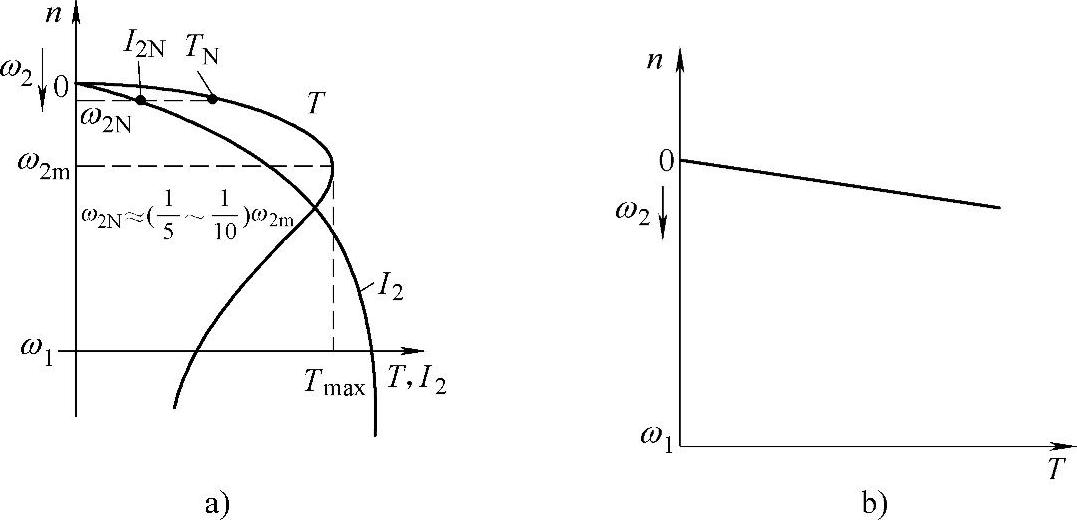
图2-44 异步电动机的转矩特性

a）以Ψ_m为参变量的转矩特性 b）以Ψ₂为参变量的转矩特性

利用通用变频器对异步电动机变频调速时，和直流调速的概念一样，在基速以下通常是恒转矩调速方式，保持电动机的主磁通Φ_m〔相当于式（2-9）中的Ψ_m〕为额定值Φ_mN不变，即Φ_m=Φ_mN。而在基速以上，则是恒功率调速方式，实际上电动机处于弱磁状态，Φ_m＜Φ_mN。

对主磁通的控制，可以通过协调式（2-9）中E₁和f₁之间的关系来实现。下面就恒转矩调速和恒功率调速方式分别进行简要的说明。

1.恒转矩调速 变频调速中，若保持E₁/f₁=C的协调控制条件，可以满足Φ_m=C的要求，实现恒转矩调速方式。

变频过程中，如果主磁通保持恒定，由它去切割转子绕组，只要得到的转差角频率ω₂=2πf₂是相同的，笼型异步电动机的转子电阻、电抗参数，转子功率因数，转子电流和电磁转矩都将保持在原有值上，不会变化。因为站在转子上看，起作用的只是主磁通的幅值和它切割转子的相对速度（∝ω₂=2πf₂），并不涉及主磁通的绝对转速（∝ω₁=2πf₁）。如果负载转矩T_L保持在额定值不变，即ω₂=ω_2N不变，不论定子频率f₁设定在什么值上，电动机都可以运行在与额定工作点相类似的最佳状态，既可被充分利用，又不致于过热。恰好满足恒转矩调速方式的要求。

保持主磁通为常数，电动机的变频人为特性的形状将保持不变，不同定子频率下的机械特性平行，且临界转矩不变。

可以想到，保持E₁/f₁=C，则Φ_m=C，电动机不会出现欠励或过励所造成的不正常情况。另外，转子电流和电磁转矩都仅由ω₂决定，从低速到高速的范围内，两者之间保持着确定的关系，电动机的功率因数和效率在调速中变化不大，都将基本保持在额定运行时的水平上。

如2.2节所述，E₁是电动机的内部电动势，难于直接检测与控制。通常是通过调整U/f函数曲线的模式来近似地保持E₁/f₁=C的关系。

2.恒功率调速 实现恒功率调速方式，也要靠协调E₁与f₁之间的关系来保证。协调控制条件是E²₁/f₁=C。

在式（2-9c）中，若保持E²₁/f₁=C，则T∝1/f₁，即Tf₁=C，异步机的电磁功率是恒定的。因此，在E²₁/f₁=C条件下，可以实现恒功率调速方式。

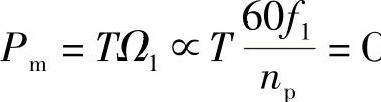
在式（2-9c）中，保持E²₁/f₁=C，随着f₁的提高，在同样的ω₂下，T将成反比地减小。反过来说，就是在同样的T值下，ω₂将增大。即随着f₁的提高，转矩特性变软。另外，对于临界点而言，T_max也随f₁的提高而成反比地减小。

当定子频率高于电动机的额定频率时，受额定电压的限制，不允许电动机的电压再提高。通常在f₁上升时，保持定子电压U₁=U_1N不变，这可以称为恒压运行方式。恒压运行方式属于近似的恒功率运行方式，说明如下。

由式（2-9c），把U₁=C近似地看成是E₁=C，则T∝1/f₁²。在ω₂保持不变时，随着f₁的上升，电磁转矩将按f₁二次方的关系迅速减小，这是问题的一个方面。另一方面，由式（2-8），当E₁=C时，I₂∝1/f₁。随着f₁的上升，T与I₂的关系不再确定不变。当f₁上升时，在ω₂不变条件下，转子电流成反比地减小，若同时考虑到f₁上升、主磁通减小还要引起电动机励磁电流I_o减小，即是说f₁上升时电动机的定子电流在ω₂不变的条件下出现了一定的裕度。这就允许在运行中适当加大转差角频率ω₂。ω₂的加大，将使电磁转矩加大。可以脱离T∝1/f₁²的关系，而向T∝1/f₁的方向靠拢。基于上述原因，人们认为恒压运行方式是近似的恒功率方式。技术资料中所说的恒功率调速一般是指恒压方式，而不是指E²₁/f₁=C。

在这种情况下，随f₁的上升，机械特性较E²₁/f₁=C的情况硬度变得更小，临界转矩也将更小。

通常情况下，上述的恒转矩调速方式、恒功率调速方式，应与机械负载的转矩特性相匹配。这种匹配关系的一个例子示于图2-45中。

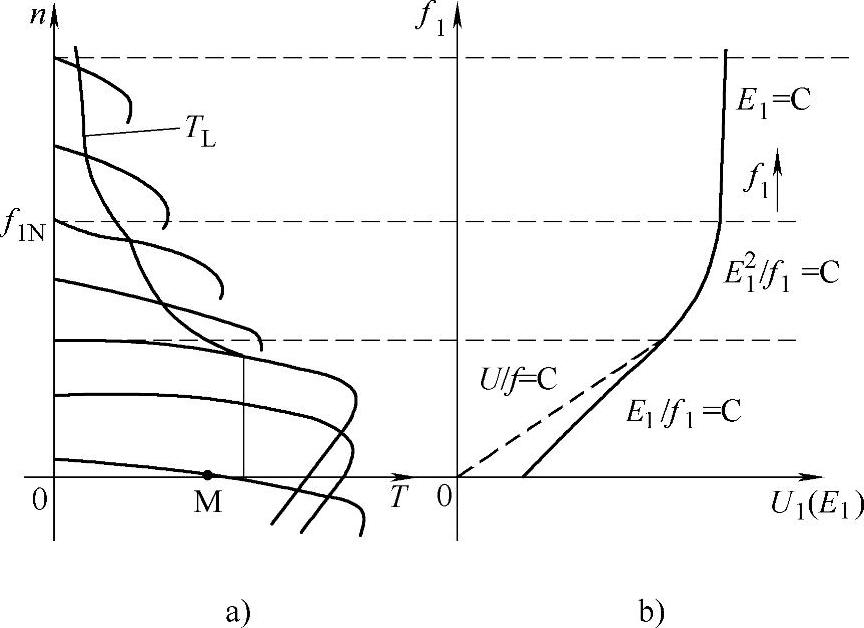
图2-45 不同调速方式下的转矩特性

a）机械特性 b）协调控制条件

由于恒功率运行和恒压运行两种方式通常是在高速区。电动机的电压U₁和感应电动势E₁的值比较大，定子漏阻抗压降相对于U₁或E₁常可以忽略不计。因此，图2-45中的协调控制条件，E²₁/f₁=C可以用U²₁/f₁=C或者U²₁/n=C（n为电动机轴转速）的关系来近似。E₁=C，f₁↑也可以用U₁=C，f₁↑来近似。